Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T15:22:42.869Z Has data issue: false hasContentIssue false
  • English
  • Français

Anisotropic wall permeability effects on turbulent channel flows

Published online by Cambridge University Press:  21 September 2018

Kazuhiko Suga Open the ORCID record for Kazuhiko Suga [Opens in a new window] ,
Yuki Okazaki ,
Unde Ho  and
Yusuke Kuwata Open the ORCID record for Yusuke Kuwata [Opens in a new window]
Kazuhiko Suga*
Affiliation:
Department of Mechanical Engineering, Osaka Prefecture University, Osaka 599-8531, Japan
Yuki Okazaki
Affiliation:
Department of Mechanical Engineering, Osaka Prefecture University, Osaka 599-8531, Japan
Unde Ho
Affiliation:
Department of Mechanical Engineering, Osaka Prefecture University, Osaka 599-8531, Japan
Yusuke Kuwata
Affiliation:
Department of Mechanical Engineering, Osaka Prefecture University, Osaka 599-8531, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Streamwise–wall-normal ($x$–$y$) and streamwise–spanwise ($x$–$z$) plane measurements are carried out by planar particle image velocimetry for turbulent channel flows over anisotropic porous media at the bulk Reynolds number 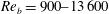$Re_{b}=900{-}13\,600$. Three kinds of anisotropic porous media are constructed to form the bottom wall of the channel. Their wall permeability tensor is designed to have a larger wall-normal diagonal component (wall-normal permeability) than the other components. Those porous media are constructed to have three mutually orthogonal principal axes and those principal axes are aligned with the Cartesian coordinate axes of the flow geometry. Correspondingly, the permeability tensor of each porous medium is diagonal. With the $x$–$y$ plane data, it is found that the turbulence level well accords with the order of the streamwise diagonal component of the permeability tensor (streamwise permeability). This confirms that the turbulence strength depends on the streamwise permeability rather than the wall-normal permeability when the permeability tensor is diagonal and the wall-normal permeability is larger than the streamwise permeability. To generally characterize those phenomena including isotropic porous wall cases, modified permeability Reynolds numbers are discussed. From a quadrant analysis, it is found that the contribution from sweeps and ejections to the Reynolds shear stress near the porous media is influenced by the streamwise permeability. In the $x$–$z$ plane data, although low- and high-speed streaks are also observed near the anisotropic porous walls, large-scale spanwise patterns appear at a larger Reynolds number. It is confirmed that they are due to the transverse waves induced by the Kelvin–Helmholtz instability. By the two-point correlation analyses of the fluctuating velocities, the spacing of the streaks and the wavelengths of the Kelvin–Helmholtz (K–H) waves are discussed. It is then confirmed that the transition point from the quasi-streak structure to the roll-cell-like structure is characterized by the wall-normal distance including the zero-plane displacement of the log-law velocity which can be characterized by the streamwise permeability. It is also confirmed that the normalized wavelengths of the K–H waves over porous media are in a similar range to that of the turbulent mixing layers irrespective of the anisotropy of the porous media.

JFM classification

Low-Reynolds-number flows: Porous media Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , pp. 983 - 1016
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Best, A. C.1935 Transfer of heat and momentum in the lowest layers of the atmosphere. Geophysical Memoirs no. 65. Meteorological Office, London.Google Scholar
Breugem, W. P., Boersma, B. J. & Uittenbogaard, R. E. 2006 The influence of wall permeability on turbulent channel flow. J. Fluid Mech. 562, 35–72.Google Scholar
Camporeale, C., Mantelli, E. & Manes, C. 2013 Interplay among unstable modes in films over permeable walls. J. Fluid Mech. 719, 527–550.Google Scholar
Carman, P. C. 1937 Fluid flow through granular beds. Trans. Inst. Chem. Engrs 15, 150–166.Google Scholar
Carman, P. C. 1956 Flow of Gases through Porous Media. Butterworth.Google Scholar
Case, C. M. & Cochran, G. F. 1972 Transformation of the tensor form of Darcy’s law in inhomogeneous and anisotropic soils. Water Resour. Res. 8, 728–733.Google Scholar
Chan, A. W., Larive, D. E. & Morgan, R. J. 1993 Anisotropic permeability of fiber preforms: constant flow rate measurement. J. Compos. Mater. 27, 996–1008.Google Scholar
Chandesris, M., D’Hueppe, A., Mathieu, B., Jamet, D. & Goyeau, B. 2013 Direct numerical simulation of turbulent heat transfer in a fluid-porous domain. Phys. Fluids 25 (12), 125110.Google Scholar
Darcy, H. 1856 Les Fontaines Publiques de la Ville de Dijon. Dalmont.Google Scholar
Detert, M., Nikora, V. & Jirka, G. H. 2010 Synoptic velocity and pressure fields at the water–sediment interface of streambeds. J. Fluid Mech. 660, 55–86.Google Scholar
Dimotakis, P. E. & Brown, G. L. 1976 The mixing layer at high Reynolds number: large-structure dynamics and entrainment. J. Fluid Mech. 78, 535–560.Google Scholar
Dullien, F. A. L. 1979 Porous Media: Fluid Transport and Pore Structure. Academic Press.Google Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32, 519–571.Google Scholar
Ghisalberti, M. & Nepf, H. 2002 Mixing layers and coherent structures in vegetated aquatic flows. J. Geophys. Res. Oceans 107 (C2), 1–11.Google Scholar
Guin, J. A., Kessler, D. P. & Greenkorn, R. A. 1971 The permeability tensor for anisotropic nonuniform porous media. Chem. Engng Sci. 26, 1475–1478.Google Scholar
Hazen, A.1892 Physical properties of sands and gravels with reference to use in filtration. Tech. Rep. 539. Massachusetts State Board of Health.Google Scholar
Ho, R. T. & Gelhar, L. W. 1973 Turbulent flow with wavy permeable boundaries. J. Fluid Mech. 58, 403–414.Google Scholar
Host-Madsen, A. & McCluskey, D. R. 1994 On the accuracy and reliability of PIV measurements. In 7th International Symposium on Application of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, pp. 214–226.Google Scholar
Iritani, Y., Kasagi, N. & Hirata, M. 1985 Heat transfer mechanism and associated turbulence structure in the near-wall region of a turbulent boundary layer. Turbulent Shear Flows 4, 2223–2234.Google Scholar
Jiménez, J., Uhlmann, M., Pinelli, A. & Kawahara, G. 2001 Turbulent shear flow over active and passive porous surfaces. J. Fluid Mech. 442, 89–117.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kong, F. Y. & Schetz, J. A.1982 Turbulent boundary layer over porous surfaces with different surface geometries. Tech. Rep. 82-0030. AIAA.Google Scholar
Kozeny, J. 1927 Ueber kapillare Leitung des Wassers im Boden. Sitzungsber Akad. Wiss., Wien 136 (2a), 271–306.Google Scholar
Kuwata, Y. & Suga, K. 2015 Progress in the extension of a second-moment closure for turbulent environmental flows. Intl J. Heat Fluid Flow 51, 268–284.Google Scholar
Kuwata, Y. & Suga, K. 2016a Lattice Boltzmann direct numerical simulation of interface turbulence over porous and rough walls. Intl J. Heat Fluid Flow 61, 145–157.Google Scholar
Kuwata, Y. & Suga, K. 2016b Transport mechanism of interface turbulence over porous and rough walls. Flow Turbul. Combust. 97, 1071–1093.Google Scholar
Kuwata, Y. & Suga, K. 2017 Direct numerical simulation of turbulence over anisotropic porous media. J. Fluid Mech. 831, 41–71.Google Scholar
Kuwata, Y., Suga, K. & Sakurai, Y. 2014 Development and application of a multi-scale k–𝜀 model for turbulent porous medium flows. Intl J. Heat Fluid Flow 49, 135–150.Google Scholar
Lovera, F. & Kennedy, J. F. 1969 Friction factors for flat bed flows in sand channels. J. Hydraul. Div. ASCE 95, 1227–1234.Google Scholar
Macdonald, I. F., El-Sayed, M. S., Mow, K. & Dullen, F. A. L. 1979 Flow through porous media: the Ergun equation revisited. Ind. Engng Chem. Fundam. 3, 199–208.Google Scholar
Manes, C., Poggi, D. & Ridol, L 2011 Turbulent boundary layers over permeable walls: scaling and near-wall structure. J. Fluid Mech. 687, 141–170.Google Scholar
Manes, C., Pokrajac, D., McEwan, I. & Nikora, V. 2009 Turbulence structure of open channel flows over permeable and impermeable beds: a comparative study. Phys. Fluids 21 (12), 125109.Google Scholar
Matsuo, T., Okabe, R., Kaneda, M. & Suga, K. 2017 Effect of anisotropic permeability on turbulent flows under porous interfaces. In Proceedings of the 16th European Turbulence Conference, Stockholm, Sweden.Google Scholar
Nakayama, A., Kuwahara, F., Umemoto, T. & Hayashi, T. 2002 Heat and fluid flow within an anisotropic porous medium. J. Heat Transfer 124, 746–753.Google Scholar
Nepf, H. & Ghisalberti, M. 2008 Flow and transport in channels with submerged vegetation. Acta Geophys. 56, 753–777.Google Scholar
Nezu, I. & Sanjou, M. 2008 Turbulence structure and coherent motion in vegetated canopy open-channel flows. J. Hydro-environ. Res. 2, 62–90.Google Scholar
Nikora, V., Koll, K., McLean, S., Dittrich, A. & Aberle, J. 2002 Zero-plane displacement for rough-bed open-channel flows. In International Conference on Fluvial Hydraulics River Flow 2002, Louvain-la-Neuve, Belgium, pp. 83–92.Google Scholar
Pedras, M. H. J. & de Lemos, M. J. S. 2000 On the definition of turbulent kinetic energy for flow in porous media. Intl Commun. Heat Mass Transfer 27 (2), 211–220.Google Scholar
Pinson, F., Grégoire, O. & Simonin, O. 2006 k–𝜀 macro-scale modeling of turbulence based on a two scale analysis in porous media. Intl J. Heat Fluid Flow 27 (5), 955–966.Google Scholar
Poggi, D., Porporato, A., Ridolfi, L., Albertson, J. D. & Katul, G. G. 2004 The effect of vegetation density on canopy sub-layer turbulence. Boundary-Layer Meteorol. 111 (3), 565–587.Google Scholar
Pokrajac, D. & Manes, C. 2009 Velocity measurements of a free-surface turbulent flow penetrating a porous medium composed of uniform-size spheres. Transp. Porous Med. 78, 367–383.Google Scholar
Prasad, A. K., Adrian, R. J., Landreth, C. C. & Offutt, P. W. 1992 Effect of resolution on the speed and accuracy of particle image velocimetry interrogation. Exp. Fluids 13, 105–116.Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44, 1–25.Google Scholar
Raupach, M. R., Finnigan, J. J. & Brunei, Y. 1996 Coherent eddies and turbulence in vegetation canopies: the mixing-layer analogy. Boundary-Layer Meteorol. 78 (3–4), 351–382.Google Scholar
Raupach, M. R. & Shaw, R. H. 1982 Averaging procedures for flow within vegetation canopies. Boundary-Layer Meteorol. 22, 79–90.Google Scholar
Rogers, M. M. & Moser, R. D. 1994 Direct simulation of a self-similar turbulent mixing layer. Phys. Fluids 6, 903–923.Google Scholar
Rosti, M. E., Cortelezzi, L. & Quadrio, M. 2015 Direct numerical simulation of turbulent channel flow over porous walls. J. Fluid Mech. 784, 396–442.Google Scholar
Ruff, J. F. & Gelhar, L. W. 1972 Turbulent shear flow in porous boundary. J. Engng Mech. Div. ASCE 98, 975–991.Google Scholar
Shimizu, Y., Tsujimoto, T. & Nakagawa, H. 1990 Experiment and macroscopic modelling of flow in highly permeable porous medium under free-surface flow. J. Hydrosci. Hydraul. Engng 8, 69–78.Google Scholar
Smith, C. R. & Metzler, S. P. 1983 The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 129, 27–54.Google Scholar
Suga, K. 2016 Understanding and modelling turbulence over and inside porous media. Flow Turbul. Combust. 96, 717–756.Google Scholar
Suga, K., Matsumura, Y., Ashitaka, Y., Tominaga, S. & Kaneda, M. 2010 Effects of wall permeability on turbulence. Intl J. Heat Fluid Flow 31, 974–984.Google Scholar
Suga, K., Mori, M. & Kaneda, M. 2011 Vortex structure of turbulence over permeable walls. Intl J. Heat Fluid Flow 32, 586–595.Google Scholar
Suga, K., Nakagawa, Y. & Kaneda, M. 2017 Spanwise turbulence structure over permeable walls. J. Fluid Mech. 822, 186–201.Google Scholar
Suga, K., Tominaga, S., Mori, M. & Kaneda, M. 2013 Turbulence characteristics in flows over solid and porous square ribs mounted on porous walls. Flow Turbul. Combust. 91, 19–40.Google Scholar
Szabo, B. A. 1968 Permeability of orthotropic porous mediums. Water Resour. Res. 4, 801–808.Google Scholar
Tilton, N. & Cortelezzi, L. 2008 Linear stability analysis of pressure-driven flows in channels with porous walls. J. Fluid Mech. 604, 411–445.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54, 39–48.Google Scholar
Whitaker, S. 1969 Advances in theory of fluid motion in porous media. Ind. Engng Chem. 61, 14–28.Google Scholar
Whitaker, S. 1986 Flow in porous media. Part I. A theoretical derivation of Darcy’s law. Trans. Porous Med. 1, 3–25.Google Scholar
Whitaker, S. 1996 The Forchheimer equation: a theoretical development. Trans. Porous Med. 25, 27–61.Google Scholar
Willert, C. E. & Gharib, M. 1991 Digital particle image velocimetry. Exp. Fluids 10, 181–193.Google Scholar
Zagni, A. F. E. & Smith, K. V. H. 1976 Channel flow over permeable beds of graded spheres. J. Hydraul. Div. ASCE 102, 207–222.Google Scholar
Zippe, H. J. & Graf, W. H. 1983 Turbulent boundary-layer flow over permeable and non-permeable rough surfaces. J. Hydraul. Res. 21, 51–65.Google Scholar