Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-30T20:43:47.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of axisymmetric boundary layers

Published online by Cambridge University Press:  26 June 2018

Praveen Kumar Open the ORCID record for Praveen Kumar [Opens in a new window]  and
Krishnan Mahesh Open the ORCID record for Krishnan Mahesh [Opens in a new window]
Praveen Kumar
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Krishnan Mahesh*
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

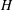Axisymmetric boundary layers are studied using integral analysis of the governing equations for axial flow over a circular cylinder. The analysis includes the effect of pressure gradient and focuses on the effect of transverse curvature on boundary layer parameters such as shape factor ($H$) and skin-friction coefficient (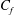$C_{f}$), defined as 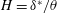$H=\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D703}$ and 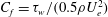$C_{f}=\unicode[STIX]{x1D70F}_{w}/(0.5\unicode[STIX]{x1D70C}U_{e}^{2})$ respectively, where 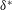$\unicode[STIX]{x1D6FF}^{\ast }$ is displacement thickness, 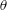$\unicode[STIX]{x1D703}$ is momentum thickness, 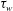$\unicode[STIX]{x1D70F}_{w}$ is the shear stress at the wall, 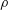$\unicode[STIX]{x1D70C}$ is density and 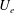$U_{e}$ is the streamwise velocity at the edge of the boundary layer. Relations are obtained relating the mean wall-normal velocity at the edge of the boundary layer (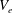$V_{e}$) and 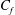$C_{f}$ to the boundary layer and pressure gradient parameters. The analytical relations reduce to established results for planar boundary layers in the limit of infinite radius of curvature. The relations are used to obtain 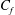$C_{f}$ which shows good agreement with the data reported in the literature. The analytical results are used to discuss different flow regimes of axisymmetric boundary layers in the presence of pressure gradients.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 927 - 941
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afzal, N. 1983 Analysis of a turbulent boundary layer subjected to a strong adverse pressure gradient. Intl J. Engng Sci. 21 (6), 563–576.Google Scholar
Afzal, N. 2008 Turbulent boundary layer with negligible wall stress. Trans. ASME J. Fluids Engng 130 (5), 051205.Google Scholar
Afzal, N. & Narasimha, R. 1976 Axisymmetric turbulent boundary layer along a circular cylinder at constant pressure. J. Fluid Mech. 74 (1), 113–128.Google Scholar
Cebeci, T. 1970 Laminar and turbulent incompressible boundary layers on slender bodies of revolution in axial flow. Trans. ASME J. Basic Engng 92, 545–554.Google Scholar
Chase, D. M. 1972 Mean velocity profile of a thick turbulent boundary layer along a circular cylinder. AIAA J. 10 (7), 849–850.Google Scholar
Clauser, F. H. 1954 Turbulent boundary layers in adverse pressure gradients. J. Aeronaut. Sci. 21 (2), 91–108.Google Scholar
Fernholz, H. H. & Warnack, D. 1998 The effects of a favourable pressure gradient and of the Reynolds number on an incompressible axisymmetric turbulent boundary layer. Part 1. The turbulent boundary layer. J. Fluid Mech. 359, 329–356.Google Scholar
Glauert, M. B. & Lighthill, M. J. 1955 The axisymmetric boundary layer on a long thin cylinder. Proc. R. Soc. Lond. A 230, 188–203.Google Scholar
Groves, N. C., Huang, T. T. & Chang, M. S. 1989 Geometric Characteristics of DARPA Suboff Models: (DTRC Model Nos. 5470 and 5471). David Taylor Research Center.Google Scholar
Jordan, S. A. 2011 Axisymmetric turbulent statistics of long slender circular cylinders. Phys. Fluids 23 (7), 075105.Google Scholar
Jordan, S. A. 2013 A skin friction model for axisymmetric turbulent boundary layers along long thin circular cylinders. Phys. Fluids 25 (7), 075104.Google Scholar
Jordan, S. A. 2014a On the axisymmetric turbulent boundary layer growth along long thin circular cylinders. J. Fluids Engng 136 (5), 051202.Google Scholar
Jordan, S. A. 2014b A simple model of axisymmetric turbulent boundary layers along long thin circular cylinders. Phys. Fluids 26 (8), 085110.Google Scholar
Kelly, H. R. 1954 A note on the laminar boundary layer on a circular cylinder in axial incompressible flow. J. Aeronaut. Sci. 21 (9), 634.Google Scholar
Krane, M. H., Grega, L. M. & Wei, T. 2010 Measurements in the near-wall region of a boundary layer over a wall with large transverse curvature. J. Fluid Mech. 664, 33–50.Google Scholar
Kumar, P. & Mahesh, K. 2016 Towards large eddy simulation of hull-attached propeller in crashback. In Proceedings of the 31st Symposium on Naval Hydrodynamics, Monterey, USA.Google Scholar
Landweber, L.1949 Effect of transverse curvature on frictional resistance. Tech. Rep. David Taylor Model Basin, Washington DC.Google Scholar
Launder, B. E. 1964 Laminarization of the turbulent boundary layer in a severe acceleration. Trans. ASME J. Appl. Mech. 31 (4), 707–708.Google Scholar
Lueptow, R. M. 1990 Turbulent boundary layer on a cylinder in axial flow. AIAA J. 28 (10), 1705–1706.Google Scholar
Lueptow, R. M., Leehey, P. & Stellinger, T. 1985 The thick, turbulent boundary layer on a cylinder: mean and fluctuating velocities. Phys. Fluids 28 (12), 3495–3505.Google Scholar
Luxton, R. E., Bull, M. K. & Rajagopalan, S. 1984 The thick turbulent boundary layer on a long fine cylinder in axial flow. Aeronaut. J. 88, 186–199.Google Scholar
Maciel, Y., Rossignol, K.-S. & Lemay, J. 2006 Self-similarity in the outer region of adverse-pressure-gradient turbulent boundary layers. AIAA J. 44 (11), 2450–2464.Google Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2008 Comparison of mean flow similarity laws in zero pressure gradient turbulent boundary layers. Phys. Fluids 20 (10), 105102.Google Scholar
Monte, S., Sagaut, P. & Gomez, T. 2011 Analysis of turbulent skin friction generated in flow along a cylinder. Phys. Fluids 23 (6), 065106.Google Scholar
Narasimha, R. & Sreenivasan, K. R. 1973 Relaminarization in highly accelerated turbulent boundary layers. J. Fluid Mech. 61 (3), 417–447.Google Scholar
Österlund, J. M.1999 Experimental studies of zero pressure-gradient turbulent boundary layer flow. PhD thesis, Royal Institute of Technology, Stockholm, Sweden.Google Scholar
Patel, V. C. 1974 A simple integral method for the calculation of thick axisymmetric turbulent boundary layers. Aeronaut. Q. 25 (1), 47–58.Google Scholar
Patel, V. C., Nakayama, A. & Damian, R. 1974 Measurements in the thick axisymmetric turbulent boundary layer near the tail of a body of revolution. J. Fluid Mech. 63 (2), 345–367.Google Scholar
Piquet, J. & Patel, V. C. 1999 Transverse curvature effects in turbulent boundary layer. Prog. Aerosp. Sci. 35 (7), 661–672.Google Scholar
Rao, G. N. V. 1967 The law of the wall in a thick axi-symmetric turbulent boundary layer. Trans. ASME J. Appl. Mech. 89, 237–338.Google Scholar
Rao, G. N. V. & Keshavan, N. R. 1972 Axisymmetric turbulent boundary layers in zero pressure-gradient flows. J. Appl. Mech. 39 (1), 25–32.Google Scholar
Richmond, R. L.1957 Experimental investigation of thick, axially symmetric boundary layers on cylinders at subsonic and hypersonic speeds. PhD thesis, California Institute of Technology.Google Scholar
Rotta, J.1953 On the theory of the turbulent boundary layer. NACA Tech. Mem. 1344.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Schlichting, H. 1968 Boundary-Layer Theory, 6th edn. McGraw-Hill.Google Scholar
Seban, R. A. & Bond, R. 1951 Skin–friction and heat-transfer characteristics of a laminar boundary layer on a cylinder in axial incompressible flow. J. Aeronaut. Sci. 18 (10), 671–675.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Stewartson, K. 1955 The asymptotic boundary layer on a circular cylinder in axial incompressible flow. Q. Appl. Maths 13 (2), 113–122.Google Scholar
Tutty, O. R. 2008 Flow along a long thin cylinder. J. Fluid Mech. 602, 1–37.Google Scholar
Warnack, D. & Fernholz, H. H. 1998 The effects of a favourable pressure gradient and of the Reynolds number on an incompressible axisymmetric turbulent boundary layer. Part 2. The boundary layer with relaminarization. J. Fluid Mech. 359, 357–381.Google Scholar
Wei, T. & Klewicki, J. 2016 Scaling properties of the mean wall-normal velocity in zero-pressure-gradient boundary layers. Phys. Rev. Fluids 1 (8), 082401.Google Scholar
Wei, T., Maciel, Y. & Klewicki, J. 2017 Integral analysis of boundary layer flows with pressure gradient. Phys. Rev. Fluids 2 (9), 092601.Google Scholar
Willmarth, W. W., Winkel, R. E., Sharma, L. K. & Bogar, T. J. 1976 Axially symmetric turbulent boundary layers on cylinders: mean velocity profiles and wall pressure fluctuations. J. Fluid Mech. 76 (01), 35–64.Google Scholar
Woods, M. J. 2006 Computation of Axial and Near-axial Flow over a Long Circular Cylinder. University of Adelaide.Google Scholar
Yu, Y. S. 1958 Effects of transverse curvature on turbulent boundary layer characteristics. J. Ship Res. 3, 33–41.Google Scholar