Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-01T03:42:28.072Z Has data issue: false hasContentIssue false
  • English
  • Français

An investigation of the mechanisms of sound generation in initially laminar subsonic jets using the Goldstein acoustic analogy

Published online by Cambridge University Press:  02 January 2013

Sergey Karabasov ,
Christophe Bogey  and
Tom Hynes
Sergey Karabasov
Affiliation:
Whittle Laboratory, Department of Engineering, University of Cambridge, Cambridge CB3 0DY, UK
Christophe Bogey
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, UMR CNRS 5509, Ecole Centrale de Lyon, Université de Lyon, 69134 Ecully, France
Tom Hynes
Affiliation:
Whittle Laboratory, Department of Engineering, University of Cambridge, Cambridge CB3 0DY, UK
Get access Rights & Permissions [Opens in a new window]

Abstract

The details of the sound sources within two initially laminar subsonic jets corresponding to different inflow conditions, one fully laminar and the other with nozzle boundary layer forcing, are studied using the Goldstein acoustic analogy. The statistics of the acoustic analogy equivalent sources are generated from large eddy simulations (LES) and issues associated with the range of validity of these are explored. The predicted comparative importance of various source terms confirms the results of previous studies, with the exception of one extra term that involves the longitudinal and the lateral source components. 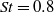Agreement within 1 dB over the frequency range from Strouhal number $\mathit{St}= 0. 8$ to 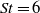$\mathit{St}= 6$, which was shown to best correspond to the validity range of the acoustic source model for the LES data available, is found between noise predictions using the acoustic analogy model and those of a previously conducted LES–ILEE (isotropic linearized Euler equation) control surface method for the nominally laminar inflow jet case. The acoustic analogy is used to determine the source length scales which contribute to noise at different radiated angles to the jet, how they are distributed and how they change with change of inflow conditions. For the vortex pairing frequency, using a new acoustic source decomposition technique based on the correlation length scale, two types of noise sources are found. One source, which corresponds to the peak source amplitude, is located at the upstream end of the jet and is associated with the vortex pairing. The other one, which is the dominant source, is associated with jet mixing at the end of the jet potential core. It is also shown that boundary layer forcing leads to a reduction in the contribution to the noise of the large source length scales in comparison with the fully laminar case.

JFM classification

Acoustics: Acoustics Acoustics: Aeroacoustics Acoustics: Jet noise
Type
Papers
Information
Journal of Fluid Mechanics , Volume 714 , 10 January 2013 , pp. 24 - 57
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afsar, M. Z. 2010 Asymptotic properties of the overall sound pressure level of sub-sonic air jets using isotropy as a paradigm. J. Fluid Mech. 664, 510–539.Google Scholar
Bogey, C. & Bailly, C. 2005 Effects of inflow conditions and forcing on a Mach 0.9 jet and its radiated noise. AIAA J. 43 (5), 1000–1007.Google Scholar
Bogey, C. & Bailly, C. 2009 Turbulence and energy budget in a self-preserving round jet: direct evaluation using large-eddy simulation. J. Fluid Mech. 627, 129–160.Google Scholar
Bogey, C. & Bailly, C. 2010 Influence of nozzle-exit boundary-layer conditions on the flow and acoustic fields of initially laminar jets. J. Fluid Mech. 663, 507–540.Google Scholar
Bogey, C., Marsden, O. & Bailly, C. 2011a Large-eddy simulation of the flow and acoustic fields of a Reynolds number 10e5 subsonic jet with tripped exit boundary layers. Phys. Fluids 23 (3), 035104.CrossRefGoogle Scholar
Bogey, C., Marsden, O. & Bailly, C. 2011b Influence of initial turbulence level on the flow and sound fields of a subsonic jet at a diameter-based Reynolds number of 10e5. J. Fluid Mech. (submitted). See also AIAA Paper 2011-2837.Google Scholar
Bridges, J. E. & Hussain, A. K. M. F. 1987 Roles of initial conditions and vortex pairing in jet noise. J. Sound Vib. 117 (2), 289–311.CrossRefGoogle Scholar
Colonius, T. & Lele, S. K. 2004 Computational aeroacoustics: progress on nonlinear problems of sound generation. Prog. Aerosp. Sci. 40, 345–416.Google Scholar
Crighton, D. G. 1981 Acoustics as a branch of fluid mechanics. J. Fluid Mech. 106, 261–298.CrossRefGoogle Scholar
Ffowcs Williams, J. E. 1963 The noise from turbulence convected at high speed. Phil. Trans. R. Soc. Lond. A 255, 469–503.Google Scholar
Goldstein, M. E. 2002 A unified approach to some recent developments in jet noise theory. Intl J. Aeroacoust. 1 (1), 1–16.Google Scholar
Goldstein, M. E. 2003 A generalized acoustic analogy. J. Fluid Mech. 488, 315–333.Google Scholar
Goldstein, M. E. 2011 Recent developments in the application of the generalized acoustic analogy to jet noise prediction. Intl J. Aeroacoust. 10 (2,3), 89–116.Google Scholar
Goldstein, M. E. & Leib, S. J. 2008 The aero-acoustics of slowly diverging supersonic jets. J. Fluid Mech. 600, 291–337.Google Scholar
Goldstein, M. E. & Rosenbaum, B. 1973 Effect of anisotropic turbulence on aerodynamic noise. J. Acoust. Soc. Am. 54, 630–645.Google Scholar
Grosche, F.-R. 1974 Distributions of sound source intensities in subsonic and supersonic jets. AGARD-CP-131, 4-1–4-10. AGARD.Google Scholar
Howe, M. S. 2003 Theory of Vortex Sound. Cambridge University Press.Google Scholar
Hill, W. G., Jenkins, R. C. & Gilbert, B. L. 1976 Effects of the initial boundary-layer state on turbulent jet mixing. AIAA J. 14 (11), 1513–1514.Google Scholar
Karabasov, S. A. 2010 Understanding jet noise. Phil. Trans. R. Soc. Lond. A 368, 3593–3608.Google Scholar
Karabasov, S. A., Afsar, M. Z., Hynes, T. P., Dowling, A. P., McMullan, W. A., Pokora, C. D., Page, G. J. & McGuirk, J. J. 2010 Jet noise: acoustic analogy informed by large eddy simulation. AIAA J. 48 (7), 1312–1325.CrossRefGoogle Scholar
Karabasov, S. A., Bogey, C. & Hynes, T. P. 2011 Computation of the noise of initially laminar jets using a statistical approach for the acoustic analogy: application and discussion. AIAA Paper 2011-2929.CrossRefGoogle Scholar
Karabasov, S. A. & Hynes, T. P. 2006 Adjoint linearized Euler solver in the frequency domain for jet noise modelling. AIAA Paper 2006-2673.Google Scholar
Khavaran, A., Bridges, J. & Georgiadis, N. 2005 Prediction of turbulence-generated noise in unheated jets. NASA TM 2005-213827.Google Scholar
Lighthill, M. J. 1952 On sound generated aerodynamically: I. General theory. Proc. R. Soc. Lond. A 222, 564–587.Google Scholar
Lilley, G. M. 1958 On the noise from air jets. Aeronaut. Res. Counc. R & M 20, 376.Google Scholar
Lilley, G. M. 1972 Generation of sound in a mixing region, Lockheed Aircraft Co. 4th Monthly progress report on contract F-33615-71-C-1663, Marietta.Google Scholar
Maestrello, L. & McDaid, E. 1971 Acoustic characteristics of a high-subsonic jet. AIAA J. 9 (6), 1058–1066.CrossRefGoogle Scholar
Michalke, A. 1971 Instabilität eines kompressiblem runden Freistrahls unter Berücksichtigung des Einflusses der Strahlgrenzschichtdicke. Z. Flugwiss. 19, 319–328 English Translation: NASA TM 75190 (1977).Google Scholar
Michalke, A. 1977 On the effect of spatial source coherence on the radiation of jet noise. J. Sound Vib. 55, 377–394.Google Scholar
Michel, U. 2009 The role of source interference in jet noise. In AIAA Paper 2009-3377.Google Scholar
Morris, P. J. 2009 A note on noise generation by large-scale turbulent structures in subsonic and supersonic jets. Intl J. Aeroacoust. 8 (4), 301–316.CrossRefGoogle Scholar
Morris, P. J. & Farassat, F. 2002 Acoustic analogy and alternative theories for jet noise prediction. AIAA J. 40, 671–680.CrossRefGoogle Scholar
Morris, P. J. & Zaman, K. B. M. Q. 2010 Velocity measurements in jets with application to noise source modelling. J. Sound Vib. 329 (4), 394–414.Google Scholar
Power, O., Kerherve, F., Fitzpatrick, J. & Jordan, P. 2004 Measurements of turbulence statistics in high subsonic jets. AIAA Paper 2004-3021.Google Scholar
Ribner, H. S. 1964 The generation of sound by turbulent jets. Adv. Appl. Mech. 8, 108–182.Google Scholar
Samanta, A., Freund, J. B., Wei, M. & Lele, S. K. 2006 Robustness of acoustic analogies for predicting mixing-layer noise. AIAA J. 44, 2780–2786.Google Scholar
Stanley, S. A. & Sarkar, S. 2000 Influence of nozzle conditions and discrete forcing on turbulent planar jets. AIAA J. 38 (9), 1615–1623.Google Scholar
Tam, C. K. W. & Auriault, L. 1998 Mean flow refraction effects on sound from localized sources in a jet. J. Fluid Mech. 370, 149–174.Google Scholar
Tam, C. K. W. & Auriault, L. 1999 Jet mixing noise from fine scale turbulence. AIAA J. 22 (2), 145–153.CrossRefGoogle Scholar
Tam, C. K. W., Golebiowski, M. & Seiner, J. M. 1996 Two components of turbulent mixing noise from supersonic jets. AIAA Paper 96-1716.Google Scholar
Tam, C. K. W., Viswanathan, K., Ahuja, K. K. & Panda, J. 2008 The sources of jet noise: experimental evidence. J. Fluid Mech. 615, 253–992.Google Scholar
Tester, B. J. & Morfey, C. L. 1976 Development in jet noise modelling – Theoretical predictions and comparisons with measured data. J. Sound Vib. 46, 79–103.Google Scholar
Viswanathan, K. 2009 Mechanisms of jet noise generation: classical theories and recent developments. Intl J. Aeroacoust. 8 (4), 355–407.Google Scholar
Xia, H., Tucker, P. G. & Eastwood, S. 2009 Large-eddy simulations of chevron jet flows with noise predictions. Intl J. Heat Fluid Flow 30 (1), 1067–1079.Google Scholar
Zaman, K. B. M. Q. 1985a Effect of initial condition on subsonic jet noise. AIAA J. 23, 1370–1373.Google Scholar
Zaman, K. B. M. Q. 1985b Far-field noise of subsonic jet under controlled excitation. J. Fluid Mech. 152, 83–111.CrossRefGoogle Scholar
Zaman, K. B. M. Q. 2011 Effect of nozzle exit conditions on subsonic jet noise, AIAA Paper 2011-2704.Google Scholar
Zaman, K. B. M. Q. & Hussain, A. K. M. F. 1980 Vortex pairing in a circular jet under controlled excitation. Part 1. General jet response. J. Fluid Mech. 101 (3), 449–491.Google Scholar