Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T04:08:53.776Z Has data issue: false hasContentIssue false
  • English
  • Français

An explicit algebraic Reynolds-stress and scalar-flux model for stably stratified flows

Published online by Cambridge University Press:  16 April 2013

W. M. J. Lazeroms ,
G. Brethouwer ,
S. Wallin  and
A. V. Johansson
W. M. J. Lazeroms*
Affiliation:
Linné FLOW Centre, Department of Mechanics, KTH Royal Institute of Technology, SE-100 44, Stockholm, Sweden
G. Brethouwer
Affiliation:
Linné FLOW Centre, Department of Mechanics, KTH Royal Institute of Technology, SE-100 44, Stockholm, Sweden
S. Wallin
Affiliation:
Linné FLOW Centre, Department of Mechanics, KTH Royal Institute of Technology, SE-100 44, Stockholm, Sweden Swedish Defence Research Agency (FOI), SE-164 90, Stockholm, Sweden
A. V. Johansson
Affiliation:
Linné FLOW Centre, Department of Mechanics, KTH Royal Institute of Technology, SE-100 44, Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This work describes the derivation of an algebraic model for the Reynolds stresses and turbulent heat flux in stably stratified turbulent flows, which are mutually coupled for this type of flow. For general two-dimensional mean flows, we present a correct way of expressing the Reynolds-stress anisotropy and the (normalized) turbulent heat flux as tensorial combinations of the mean strain rate, the mean rotation rate, the mean temperature gradient and gravity. A system of linear equations is derived for the coefficients in these expansions, which can easily be solved with computer algebra software for a specific choice of the model constants. The general model is simplified in the case of parallel mean shear flows where the temperature gradient is aligned with gravity. For this case, fully explicit and coupled expressions for the Reynolds-stress tensor and heat-flux vector are given. A self-consistent derivation of this model would, however, require finding a root of a polynomial equation of sixth-order, for which no simple analytical expression exists. Therefore, the nonlinear part of the algebraic equations is modelled through an approximation that is close to the consistent formulation. 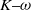By using the framework of a $K\text{{\ndash}} \omega $ model (where 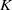$K$ is turbulent kinetic energy and 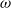$\omega $ an inverse time scale) and, where needed, near-wall corrections, the model is applied to homogeneous shear flow and turbulent channel flow, both with stable stratification. For the case of homogeneous shear flow, the model predicts a critical Richardson number of 0.25 above which the turbulent kinetic energy decays to zero. The channel-flow results agree well with DNS data. Furthermore, the model is shown to be robust and approximately self-consistent. It also fulfils the requirements of realizability.

JFM classification

Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 723 , 25 May 2013 , pp. 91 - 125
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cheng, Y., Canuto, V. M. & Howard, A. M. 2002 An improved model for the turbulent PBL. J. Atmos. Sci. 59, 1550–1565.Google Scholar
Durbin, P. A. 1993 Application of a near-wall turbulence model to boundary layers and heat transfer. Intl J. Heat Fluid Flow 14, 316–323.Google Scholar
García-Villalba, M. & del Álamo, J. C. 2011 Turbulence modification by stable stratification in channel flow. Phys. Fluids 23, 045104.Google Scholar
Girimaji, S. S. 1996 Fully explicit and self-consistent algebraic Reynolds stress model. Theor. Comput. Fluid Dyn. 8, 387–402.Google Scholar
Gullman-Strand, J. 2004 Turbulence and scalar flux modelling applied to separated flows. PhD thesis, Royal Institute of Technology, Stockholm.Google Scholar
Högström, C.-M., Wallin, S. & Johansson, A. V. 2001 Passive scalar flux modelling for CFD. In Second International Symposium on Turbulence and Shear Flow Phenomena, Stockholm (ed. Lindborg, E., Johansson, A., Eaton, J., Humphrey, J., Kasagi, N., Leschziner, M. & Sommerfeld, M.), vol. II, pp. 383–388. Stockholm.Google Scholar
Howard, L. N. 1961 Note on a paper by John W. Miles. J. Fluid Mech. 13, 158–160.Google Scholar
Jacobitz, F. G., Sarkar, S. & van Atta, C. W. 1997 Direct numerical simulations of the turbulence evolution in a uniformly sheared and stably stratified flow. J. Fluid Mech. 342, 231–261.Google Scholar
Johansson, A. V. & Wikström, P. M. 1999 DNS and modelling of passive scalar transport in turbulent channel flow with a focus on scalar dissipation rate modelling. Flow Turbul. Combust. 63, 223–245.Google Scholar
Launder, B. E. 1975 On the effects of a gravitational field on the turbulent transport of heat and momentum. J. Fluid Mech. 67, 569–581.Google Scholar
Launder, B. E., Reece, G. J. & Rodi, W. 1975 Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 68, 537–566.Google Scholar
Lumley, J. L. 1978 Computational modelling of turbulent flows. Adv. Appl. Mech. 18, 123–177.Google Scholar
Mellor, G. L. & Yamada, T. 1974 A hierarchy of turbulence closure models for planetary boundary layers. J. Atmos. Sci. 31, 1791–1806.Google Scholar
Mellor, G. L. & Yamada, T. 1982 Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys. 20, 851–875.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.Google Scholar
Peng, S.-H. & Davidson, L. 1999 Computation of turbulent buoyant flows in enclosures with low-Reynolds-number $k\text{-} \omega $ models. Intl J. Heat Fluid Flow 20, 172–184.Google Scholar
Pope, S. B. 1975 A more general effective-viscosity hypothesis. J. Fluid Mech. 72, 331–340.Google Scholar
Rodi, W. 1972 The prediction of free turbulent boundary layers by use of a two equation model of turbulence. PhD thesis, University of London.Google Scholar
Rodi, W. 1976 A new algebraic relation for calculating the Reynolds stresses. Z. Angew. Math. Mech. 56, T219–221.Google Scholar
Rodi, W. 2000 Turbulence Models and Their Applications in Hydraulics - A State-of-the-art Review. A.A. Balkema.Google Scholar
Rotta, J. 1951 Statistische Theorie nichthomogener Turbulenz. Z. Phys. 129, 547–572.Google Scholar
Shih, L. H., Koseff, J. R., Ferziger, J. H. & Rehmann, C. R. 2000 Scaling and parameterization of stratified homogeneous turbulent shear flow. J. Fluid Mech. 412, 1–20.Google Scholar
So, R. M. C., Jin, L. H. & Gatski, T. B. 2004 An explicit algebraic Reynolds stress and heat flux model for incompressible turbulence: part II Buoyant flow. Theor. Comput. Fluid Dyn. 17, 377–406.Google Scholar
So, R. M. C., Vimala, P., Jin, L. H., Zhao, C. Y. & Gatski, T. B. 2002 Accounting for buoyancy effects in the explicit algebraic stress model: homogeneous turbulent shear flows. Theor. Comput. Fluid Dyn. 15, 283–302.Google Scholar
Sommer, T. P., So, R. M. C. & Lai, Y. G. 1992 A near-wall two-equation model for turbulent heat fluxes. Intl J. Heat Mass Transfer 35, 3375–3387.Google Scholar
Taulbee, D. B., Sonnenmeier, J. R. & Wall, K. M. 1994 Stress relation for three-dimensional turbulent flows. Phys. Fluids 6, 1399–1401.Google Scholar
Violeau, D. 2009 Explicit algebraic Reynolds stresses and scalar fluxes for density-stratified shear flows. Phys. Fluids 21, 035103.Google Scholar
Wallin, S. & Johansson, A. V. 2000 An explicit algebraic Reynolds stress model for incompressible and compressible turbulent flows. J. Fluid Mech. 403, 89–132.Google Scholar
Wikström, P. M. 1998 Measurement, direct numerical simulation and modelling of passive scalar transport in turbulent flows. PhD thesis, Royal Institute of Technology, Stockholm.Google Scholar
Wikström, P. M., Wallin, S. & Johansson, A. V. 2000 Derivation and investigation of a new explicit algebraic model for the passive scalar flux. Phys. Fluids 12, 688–702.Google Scholar
Wilcox, D. C. 1993 Turbulence Modelling for CFD. DCW Industries, Inc.Google Scholar
Ying, R. & Canuto, V. M. 1996 Turbulence modelling over two-dimensional hills using an algebraic Reynolds stress expression. Boundary-Layer Meteorol. 77, 69–99.Google Scholar