Article contents
An exact Lagrangian-mean wave activity for finite-amplitude disturbances to barotropic flow on a sphere
Published online by Cambridge University Press: 12 January 2012
Abstract
The finite-amplitude Rossby wave activity introduced recently by Nakamura and co-workers measures disturbances in terms of the areal displacement of potential vorticity (PV) from zonal symmetry and possesses exact Eliassen–Palm and non-acceleration theorems. This article investigates both theoretically and numerically how this wave activity, denoted 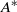 , relates to previously defined quantities such as the generalized Lagrangian-mean (GLM) pseudomomentum density and the impulse-Casimir (IC) wave activity in the context of barotropic flow on a sphere. It is shown that under the barotropic constraint both the new and GLM formalisms derive the non-acceleration theorem from the conservation of Kelvin’s circulation, but the two differ in the way the circulation is partitioned into a mean flow and wave activity/pseudomomentum density. The new wave activity differs from the (negative of) GLM pseudomomentum density by the Stokes correction to angular momentum density, which is not negligible even in the small-amplitude limit. In contrast,
, relates to previously defined quantities such as the generalized Lagrangian-mean (GLM) pseudomomentum density and the impulse-Casimir (IC) wave activity in the context of barotropic flow on a sphere. It is shown that under the barotropic constraint both the new and GLM formalisms derive the non-acceleration theorem from the conservation of Kelvin’s circulation, but the two differ in the way the circulation is partitioned into a mean flow and wave activity/pseudomomentum density. The new wave activity differs from the (negative of) GLM pseudomomentum density by the Stokes correction to angular momentum density, which is not negligible even in the small-amplitude limit. In contrast, 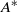 converges to the IC wave activity and the familiar linear pseudomomentum density in the conservative small-amplitude limit, provided that their reference states are identical. Both the GLM pseudomomentum density and the zonal-mean IC wave activity may be cast in a flux conservation form in equivalent latitude, which may then be related to an exact Eliassen–Palm theorem through a gauge transformation. However, of the three wave activity forms, only
converges to the IC wave activity and the familiar linear pseudomomentum density in the conservative small-amplitude limit, provided that their reference states are identical. Both the GLM pseudomomentum density and the zonal-mean IC wave activity may be cast in a flux conservation form in equivalent latitude, which may then be related to an exact Eliassen–Palm theorem through a gauge transformation. However, of the three wave activity forms, only 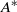 satisfies an exact non-acceleration theorem for the zonal-mean zonal wind
satisfies an exact non-acceleration theorem for the zonal-mean zonal wind 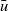 . A simple jet forcing experiment is used to examine the quantitative differences among these diagnostics. In this experiment,
. A simple jet forcing experiment is used to examine the quantitative differences among these diagnostics. In this experiment, 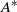 and the IC wave activity behave similarly in the domain average; however, they differ substantially in the local profiles, the former being more closely related to the flow modification. Despite their close conceptual relationship, the GLM pseudomomentum fails to capture the meridional structure of
and the IC wave activity behave similarly in the domain average; however, they differ substantially in the local profiles, the former being more closely related to the flow modification. Despite their close conceptual relationship, the GLM pseudomomentum fails to capture the meridional structure of 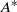 because the Stokes correction term dominates the former. This demonstrates various advantages of
because the Stokes correction term dominates the former. This demonstrates various advantages of 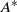 as a diagnostic of eddy–mean flow interaction.
as a diagnostic of eddy–mean flow interaction.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
Footnotes
Present address: The University of Chicago, 5734 S. Ellis Avenue, Chicago, IL 60637, USA
References
- 13
- Cited by


