Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Farazmand, Mohammad
and
Sapsis, Themistoklis P.
2016.
Dynamical indicators for the prediction of bursting phenomena in high-dimensional systems.
Physical Review E,
Vol. 94,
Issue. 3,
Budanur, Nazmi Burak
and
Cvitanović, Predrag
2017.
Unstable Manifolds of Relative Periodic Orbits in the Symmetry-Reduced State Space of the Kuramoto–Sivashinsky System.
Journal of Statistical Physics,
Vol. 167,
Issue. 3-4,
p.
636.
Olvera, D.
and
Kerswell, R. R.
2017.
Optimizing energy growth as a tool for finding exact coherent structures.
Physical Review Fluids,
Vol. 2,
Issue. 8,
Farazmand, Mohammad
and
Sapsis, Themistoklis P.
2017.
Reduced-order prediction of rogue waves in two-dimensional deep-water waves.
Journal of Computational Physics,
Vol. 340,
Issue. ,
p.
418.
Willis, A. P.
Duguet, Y.
Omel’chenko, O.
and
Wolfrum, M.
2017.
Surfing the edge: using feedback control to find nonlinear solutions.
Journal of Fluid Mechanics,
Vol. 831,
Issue. ,
p.
579.
Hiruta, Yoshiki
and
Toh, Sadayoshi
2017.
Intermittent direction reversals of moving spatially localized turbulence observed in two-dimensional Kolmogorov flow.
Physical Review E,
Vol. 96,
Issue. 6,
Lucas, Dan
and
Kerswell, Rich
2017.
Sustaining processes from recurrent flows in body-forced turbulence.
Journal of Fluid Mechanics,
Vol. 817,
Issue. ,
Budanur, N. B.
Short, K. Y.
Farazmand, M.
Willis, A. P.
and
Cvitanović, P.
2017.
Relative periodic orbits form the backbone of turbulent pipe flow.
Journal of Fluid Mechanics,
Vol. 833,
Issue. ,
p.
274.
Farazmand, Mohammad
and
Sapsis, Themistoklis P.
2017.
A variational approach to probing extreme events in turbulent dynamical systems.
Science Advances,
Vol. 3,
Issue. 9,
SMITH, W. R.
and
WISSINK, J. G.
2018.
Asymptotic analysis of the attractors in two-dimensional Kolmogorov flow.
European Journal of Applied Mathematics,
Vol. 29,
Issue. 3,
p.
393.
Suri, Balachandra
Tithof, Jeffrey
Grigoriev, Roman O.
and
Schatz, Michael F.
2018.
Unstable equilibria and invariant manifolds in quasi-two-dimensional Kolmogorov-like flow.
Physical Review E,
Vol. 98,
Issue. 2,
Sapsis, Themistoklis P.
2018.
New perspectives for the prediction and statistical quantification of extreme events in high-dimensional dynamical systems.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 376,
Issue. 2127,
p.
20170133.
Farazmand, Mohammad
and
Sapsis, Themistoklis P.
2019.
Extreme Events: Mechanisms and Prediction.
Applied Mechanics Reviews,
Vol. 71,
Issue. 5,
Blanchard, Antoine
and
Sapsis, Themistoklis P.
2019.
Stabilization of unsteady flows by reduced-order control with optimally time-dependent modes.
Physical Review Fluids,
Vol. 4,
Issue. 5,
Blanchard, Antoine
Mowlavi, Saviz
and
Sapsis, Themistoklis P.
2019.
Control of linear instabilities by dynamically consistent order reduction on optimally time-dependent modes.
Nonlinear Dynamics,
Vol. 95,
Issue. 4,
p.
2745.
Farazmand, Mohammad
and
Sapsis, Themistoklis P.
2019.
Closed-loop adaptive control of extreme events in a turbulent flow.
Physical Review E,
Vol. 100,
Issue. 3,
Budanur, Nazmi Burak
and
Fleury, Marc
2019.
State space geometry of the chaotic pilot-wave hydrodynamics.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 29,
Issue. 1,
Blonigan, Patrick J.
Farazmand, Mohammad
and
Sapsis, Themistoklis P.
2019.
Are extreme dissipation events predictable in turbulent fluid flows?.
Physical Review Fluids,
Vol. 4,
Issue. 4,
Rupe, Adam
Prabhat, Mr
Crutchfield, James P.
Kumar, Nalini
Epifanov, Vladislav
Kashinath, Karthik
Pavlyk, Oleksandr
Schlimbach, Frank
Patwary, Mostofa
Maidanov, Sergey
and
Lee, Victor
2019.
DisCo: Physics-Based Unsupervised Discovery of Coherent Structures in Spatiotemporal Systems.
p.
75.
Suri, Balachandra
Pallantla, Ravi Kumar
Schatz, Michael F.
and
Grigoriev, Roman O.
2019.
Heteroclinic and homoclinic connections in a Kolmogorov-like flow.
Physical Review E,
Vol. 100,
Issue. 1,
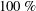 $100\,\%$ is observed, leading to the discovery of
$100\,\%$ is observed, leading to the discovery of 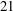 $21$ new steady-state and travelling-wave solutions at Reynolds number
$21$ new steady-state and travelling-wave solutions at Reynolds number 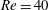 $Re=40$. Some of the new invariant solutions have spatially localized structures that were previously believed to exist only on domains with large aspect ratios. We show that one of the newly found steady-state solutions underpins the temporal intermittencies, i.e. high energy dissipation episodes of the flow. More precisely, it is shown that each intermittent episode of a generic turbulent trajectory corresponds to its close passage to this equilibrium solution.
$Re=40$. Some of the new invariant solutions have spatially localized structures that were previously believed to exist only on domains with large aspect ratios. We show that one of the newly found steady-state solutions underpins the temporal intermittencies, i.e. high energy dissipation episodes of the flow. More precisely, it is shown that each intermittent episode of a generic turbulent trajectory corresponds to its close passage to this equilibrium solution.


