Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-25T04:24:08.208Z Has data issue: false hasContentIssue false
  • English
  • Français

An active feedback flow control theory of the axisymmetric vortex breakdown process

Published online by Cambridge University Press:  15 June 2015

Zvi Rusak ,
Joshua Granata  and
Shixiao Wang
Zvi Rusak*
Affiliation:
Department of Mechanical, Aerospace, and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180-3590, USA
Joshua Granata
Affiliation:
Department of Mechanical, Aerospace, and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180-3590, USA
Shixiao Wang
Affiliation:
Department of Mathematics, University of Auckland, 38 Princes Street, Auckland, 1142, New Zealand
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An active feedback flow control theory of the axisymmetric vortex breakdown process in incompressible swirling flows in a finite-length straight circular pipe is developed. Flow injection distributed along the pipe wall is used as the controller. The flow is subjected to non-periodic inlet and outlet conditions where the inlet profiles of the axial velocity, circumferential velocity and azimuthal vorticity are prescribed, along with no radial velocity at the outlet. A long-wave asymptotic analysis at near-critical swirl ratios, which involves a rescaling of the axial distance and time, results in a model problem for the dynamics and the nonlinear control of both inviscid and high-Reynolds-number (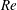$\mathit{Re}$) flows. The approach provides the bifurcation diagram of steady states and the stability characteristics of these states. In addition, an energy analysis of the controlled flow dynamics suggests a feedback control law that relates the flow injection to the evolving maximum radial velocity at the inlet. Computed examples of the flow dynamics based on the full Euler and Navier–Stokes formulations at various swirl levels demonstrate the evolution to near-steady breakdown states when swirl is above a critical level that depends on 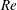$\mathit{Re}$. Moreover, applying the proposed feedback control law during flow evolution shows for the first time the successful and robust elimination of the breakdown states and flow stabilization on an almost columnar state for a wide range of swirl (up to at least 30 %) above critical. The feedback control cuts the natural feed-forward mechanism of the breakdown process. Specifically, in the case of high-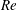$\mathit{Re}$ flows, the control approach establishes a branch of columnar states for all swirl levels studied, where in the natural flow dynamics no such states exist. The present theory is limited to the control of axisymmetric flows in pipes where the wall boundary layer is thin and attached and does not interact with the flow in the bulk.

JFM classification

Flow Control: Control theory Vortex Flows: Vortex breakdown Vortex Flows: Vortex instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 774 , 10 July 2015 , pp. 488 - 528
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1956 On steady laminar flow with closed streamlines at large Reynolds number. J. Fluid Mech. 1, 177–190.Google Scholar
Benjamin, T. B. 1962 Theory of the vortex breakdown phenomenon. J. Fluid Mech. 14, 593–629.CrossRefGoogle Scholar
Beran, P. S. 1994 The time-asymptotic behavior of vortex breakdown in tubes. Comput. Fluids 23, 913–937.Google Scholar
Beran, P. S. & Culick, F. E. C. 1992 The role of non-uniqueness in the development of vortex breakdown in tubes. J. Fluid Mech. 242, 491–527.Google Scholar
Brücker, Ch. & Althaus, W. 1995 Study of vortex breakdown by particle tracking velocimetry (PTV), Part 3: time-dependent structure and development of breakdown modes. Exp. Fluids 18, 174–186.Google Scholar
Buntine, J. D. & Saffman, P. G. 1995 Inviscid swirling flows and vortex breakdown. Proc. R. Soc. Lond. A 449 (1935), 139–153.Google Scholar
Faler, J. H. & Leibovich, S. 1977 Disrupted states of vortex flow and vortex breakdown. Phys. Fluids 20 (9), 1385–1400.Google Scholar
Gallaire, F. & Chomaz, J.-M. 2004 The role of boundary conditions in a simple model of incipient vortex breakdown. Phys. Fluids 16 (2), 274–286.CrossRefGoogle Scholar
Gallaire, F., Chomaz, J.-M. & Huerre, P. 2004 Closed-loop control of vortex breakdown: a model study. J. Fluid Mech. 511, 67–93.Google Scholar
Garg, A. K. & Leibovich, S. 1979 Spectral characteristics of vortex breakdown flow field. Phys. Fluids 22, 2053–2064.CrossRefGoogle Scholar
Granata, J.2014 An active feedback flow control theory of the vortex breakdown process. PhD dissertation, Rensselaer Polytechnic Institute, Troy, NY.Google Scholar
Grimshaw, R. & Yi, Z. 1993 Resonant generation of finite-amplitude waves by the flow of a uniformly rotating fluid past an obstacle. Mathematika 40, 30–50.Google Scholar
Hanazaki, H. 1996 On the wave excitation and the formation of recirculation eddies in an axisymmetric flow of uniformly rotating fluids. J. Fluid Mech. 322, 165–200.Google Scholar
Keller, J. J., Egli, W. & Exley, W. 1985 Force- and loss-free transitions between flow states. Z. Angew. Math. Phys. 36, 854–889.Google Scholar
Leclaire, B. & Sipp, D. 2010 A sensitivity study of vortex breakdown onset to upstream boundary conditions. J. Fluid Mech. 645, 81–119.Google Scholar
Leclaire, B., Sipp, D. & Jacquin, L. 2007 Near-critical swirling flow in a contracting duct: the case of plug axial flow with solid-body rotation. Phys. Fluids 19 (9), 091701.Google Scholar
Leibovich, S. 1984 Vortex stability and breakdown: survey and extension. AIAA J. 22, 1192–1206.Google Scholar
Leibovich, S. & Kribus, A. 1990 Large amplitude wavetrains and solitary waves in vortices. J. Fluid Mech. 216, 459–504.Google Scholar
Leibovich, S. & Randall, J. D. 1972 Solitary waves in concentrated vortices. J. Fluid Mech. 52, 625–635.Google Scholar
Liang, H. & Maxworthy, T. 2005 An experimental investigation of swirling jets. J. Fluid Mech. 525, 115–159.Google Scholar
Long, R. R. 1953 Steady motion around a symmetrical obstacle moving along the axis of a rotating liquid. J. Meteorol. 10, 197–203.2.0.CO;2>CrossRefGoogle Scholar
Lopez, J. M. 1994 On the bifurcation structure of axisymmetric vortex breakdown in a constricted pipe. Phys. Fluids 6, 3683–3693.Google Scholar
Mattner, T. W., Joubert, P. N. & Chong, M. S. 2002 Vortical flow. Part 1: Flow through a constant diameter pipe. J. Fluid Mech. 463, 259–291.Google Scholar
Meliga, P. & Gallaire, F. 2011 Control of axisymmetric vortex breakdown in a constricted pipe: nonlinear steady states and weakly nonlinear asymptotic expansions. Phys. Fluids 23, 084102.Google Scholar
Mitchell, A. M. & Delery, J. 2001 Research into vortex breakdown control. Prog. Aerosp. Sci. 37 (4), 385–418.Google Scholar
Muruganandam, T. M., Nair, S., Scarborough, D., Neumeier, Y., Jagoda, J., Lieuwen, T., Seitzman, J. & Zinn, B. 2005 Active control of lean blowout for turbine engine combustors. J. Propul. Power 21 (5), 807–814.Google Scholar
Novak, F. & Sarpkaya, T. 2000 Turbulent vortex breakdown at high Reynolds numbers. AIAA J. 38 (5), 825–834.Google Scholar
Randall, J. D. & Leibovich, S. 1973 The critical state: a trapped wave model of vortex breakdown. J. Fluid Mech. 53, 48–493.Google Scholar
Ruith, M. R., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes: direct numerical simulation. J. Fluid Mech. 486, 331–378.Google Scholar
Rusak, Z. 1996 Axisymmetric swirling flow around a vortex breakdown point. J. Fluid Mech. 323, 79–105.Google Scholar
Rusak, Z. 1998 The interaction of near-critical swirling flows in a pipe with inlet vorticity perturbations. Phys. Fluids 10 (7), 1672–1684.Google Scholar
Rusak, Z., Wang, S., Xu, L. & Taylor, S. 2012 On the global nonlinear stability of a near-critical swirling flow in a long finite-length pipe and the path to vortex breakdown. J. Fluid Mech. 712, 295–326.Google Scholar
Rusak, Z. & Wang, S. 2014 Wall-separation and vortex-breakdown zones in a solid-body rotation flow in a rotating finite-length straight circular pipe. J. Fluid Mech. 759, 321–359.Google Scholar
Sarpkaya, T. 1971 On stationary and travelling vortex breakdowns. J. Fluid Mech. 45, 545–559.Google Scholar
Sarpkaya, T. 1974 Effect of adverse pressure-gradient on vortex breakdown. AIAA J. 12 (5), 602–607.Google Scholar
Sarpkaya, T. 1995 Turbulent vortex breakdown. Phys. Fluids 7 (10), 2301–2303.Google Scholar
Squire, H. B. 1956 Rotating fluids. In Surveys in Mechanics (ed. Batchelor, G. K. & Davies, R. M.), pp. 139–161. Cambridge University Press.Google Scholar
Uchida, S., Nakamura, Y. & Ohsawa, M. 1985 Experiments on the axisymmetric vortex breakdown in a swirling air flow. Japan. Soc. Aeronaut. Space Sci. 27, 206–216.Google Scholar
Umeh, C. O. U., Rusak, Z., Gutmark, E., Villalva, R. & Cha, D. J. 2010 Experimental and computational study of nonreacting vortex breakdown in a swirl-stabilized combustor. AIAA J. 48 (11), 2576–2585.Google Scholar
Vyazmina, E., Nichols, J. W., Chomaz, J. M. & Schmid, P. J. 2009 The bifurcation structure of viscous steady axisymmetric vortex breakdown with open lateral boundaries. Phys. Fluids 21 (7), 074107.Google Scholar
Wang, S. & Rusak, Z. 1996 On the stability of an axisymmetric rotating flow in a pipe. Phys. Fluids 8 (4), 1007–1016.Google Scholar
Wang, S. & Rusak, Z. 1997a The dynamics of a swirling flow in a pipe and transition to axisymmetric vortex breakdown. J. Fluid Mech. 340, 177–223.Google Scholar
Wang, S. & Rusak, Z. 1997b The effect of slight viscosity on a near-critical swirling flow in a pipe. Phys. Fluids 9 (7), 1914–1927.Google Scholar
Wang, S. & Rusak, Z. 2011 Energy transfer mechanism of the instability of an axisymmetric swirling flow in a finite-length pipe. J. Fluid Mech. 679, 505–543.Google Scholar
Wang, S., Rusak, Z., Taylor, S. & Gong, R. 2013 On the active feedback control of a swirling flow in a finite-length pipe. J. Fluid Mech. 737, 280–307.Google Scholar
Xu, L.2012 Vortex flow stability, dynamics and feedback stabilization. PhD dissertation, Rensselaer Polytechnic Institute, Troy, NY.Google Scholar