Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T04:54:16.176Z Has data issue: false hasContentIssue false
  • English
  • Français

Amplitude modulation between multi-scale turbulent motions in high-Reynolds-number atmospheric surface layers

Published online by Cambridge University Press:  27 December 2018

Hongyou Liu Open the ORCID record for Hongyou Liu [Opens in a new window] ,
Guohua Wang  and
Xiaojing Zheng
Hongyou Liu
Affiliation:
College of Civil Engineering and Mechanics, Lanzhou University, Key Laboratory of Mechanics on Disaster and Environment in Western China, Ministry of Education of China, Lanzhou 730000, PR China
Guohua Wang*
Affiliation:
College of Civil Engineering and Mechanics, Lanzhou University, Key Laboratory of Mechanics on Disaster and Environment in Western China, Ministry of Education of China, Lanzhou 730000, PR China
Xiaojing Zheng*
Affiliation:
Research Center for Applied Mechanics, School of Mechano-Electronic Engineering, Xidian University, Xian 710071, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

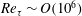Long-term measurements were performed at the Qingtu Lake Observation Array site to obtain high-Reynolds-number atmospheric surface layer flow data ($Re_{\unicode[STIX]{x1D70F}}\sim O(10^{6})$). Based on the selected high-quality data in the near-neutral surface layer, the amplitude modulation between multi-scale turbulent motions is investigated under various Reynolds number conditions. The results show that the amplitude modulation effect may exist in specific motions rather than at all length scales of motion. The most energetic motions with scales larger than the wavelength of the lower wavenumber peak in the energy spectra play a vital role in the amplitude modulation effect; the small scales shorter than the wavelength of the higher wavenumber peak are strongly modulated, whereas the motions with scales ranging between these two peaks neither contribute significantly to the amplitude modulation effect nor are strongly modulated. Based on these results, a method of decomposing the fluctuating velocity is proposed to accurately estimate the degree of amplitude modulation. The corresponding amplitude modulation coefficient is much larger than that estimated by establishing a nominal cutoff wavelength; moreover, it increases log-linearly with the Reynolds number. An empirical model is proposed to parametrize the variation of the amplitude modulation coefficient with the Reynolds number and the wall-normal distance. This study contributes to a better understanding of the interaction between multi-scale turbulent motions and the results may be used to validate and improve existing numerical models of high-Reynolds-number wall turbulence.

JFM classification

Turbulent Flows: Turbulent boundary layers Geophysical and Geological Flows: Atmospheric flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 585 - 607
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Anderson, W. 2016 Amplitude modulation of streamwise velocity fluctuations in the roughness sublayer: evidence from large-eddy simulations. J. Fluid Mech. 789, 567–588.Google Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2017 Reynolds number trend of hierarchies and scale interactions in turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 375, 20160077.Google Scholar
Bailey, S. C., Hultmark, M., Smits, A. J. & Schultz, M. P. 2008 Azimuthal structure of turbulence in high Reynolds number pipe flow. J. Fluid Mech. 615, 121–138.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large-and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google Scholar
Bandyopadhyay, P. R. & Hussain, A. K. M. F. 1984 The coupling between scales in shear flows. Phys. Fluids 27 (9), 2221–2228.Google Scholar
Brown, G. L. & Thomas, A. S. 1977 Large structure in a turbulent boundary layer. Phys. Fluids 20 (10), S243–S252.Google Scholar
Clauser, F. H. 1956 The turbulent boundary layer. Adv. Appl. Mech. 4, 1–51.Google Scholar
DeGraaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Deng, B. Q., Huang, W. X. & Xu, C. X. 2016 Origin of effectiveness degradation in active drag reduction control of turbulent channel flow at Re 𝜏 = 1000. J. Turbul. 17 (8), 758–786.Google Scholar
Dennis, D. J. 2015 Coherent structures in wall-bounded turbulence. An. Acad. Bras. Cinc. 87 (2), 1161–1193.Google Scholar
Drobinski, P., Carlotti, P., Newsom, R. K., Banta, R. M., Foster, R. C. & Redelsperger, J. L. 2004 The structure of the near-neutral atmospheric surface layer. J. Atmos. Sci. 61 (6), 699–714.Google Scholar
Foken, T., Gockede, M., Mauder, M., Mahrt, L., Amiro, B. & Munger, W. 2004 Post-field data quality control. In Handbook of Micrometeorology: A Guide for Surface Flux Measurement and Analysis (ed. Lee, X., Massman, W. & Law, B.), pp. 181–208. Kluwer Academic.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Guala, M., Metzger, M. & McKeon, B. J. 2011 Interactions within the turbulent boundary layer at high Reynolds number. J. Fluid Mech. 666, 573–604.Google Scholar
Högström, U. 1988 Non-dimensional wind and temperature profiles in the atmospheric surface layer: a re-evaluation. Boundary-Layer Meteorol. 42, 55–78.Google Scholar
Högström, U., Hunt, J. C. R. & Smedman, A. S. 2002 Theory and measurements for turbulence spectra and variances in the atmospheric neutral surface layer. Boundary-Layer Meteorol. 103 (1), 101–124.Google Scholar
Hoyas, S. & Jimnez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18 (1), 011702.Google Scholar
Hristov, T., Friehe, C. & Miller, S. 1998 Wave-coherent fields in air flow over ocean waves: identification of cooperative behavior buried in turbulence. Phys. Rev. Lett. 81 (23), 5245–5248.Google Scholar
Huang, N. E., Shen, Z. & Long, S. R. 1999 A new view of nonlinear water waves: the Hilbert spectrum. Annu. Rev. Fluid Mech. 31, 417–457.Google Scholar
Hunt, J. C. & Morrison, J. F. 2000 Eddy structure in turbulent boundary layers. Eur. J. Mech. B 19 (5), 673–694.Google Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145 (2), 273–306.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google Scholar
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Inoue, M., Mathis, R., Marusic, I. & Pullin, D. I. 2012 Wall shear-stress statistics for the turbulent boundary layer by use of a predictive wall-model with LES. 18th Australasian Fluid Mechanics Conference, Launceston.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds-number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.Google Scholar
Liu, H. Y., Bo, T. L. & Liang, Y. R. 2017 The variation of large-scale structure inclination angles in high Reynolds number atmospheric surface layers. Phys. Fluids 29 (3), 035104.Google Scholar
Luhar, M., Sharma, A. S. & McKeon, B. J. 2014 On the structure and origin of pressure fluctuations in wall turbulence: predictions based on the resolvent analysis. J. Fluid Mech. 751, 38–70.Google Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15 (8), 2461–2464.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010b Predictive model for wall-bounded turbulent flow. Science 329 (5988), 193–196.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2011 A wall-shear stress predictive model. J. Phys.: Conf. Ser. 318, 012003.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010a Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22 (6), 065103.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009a Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011a A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.Google Scholar
Mathis, R., Marusic, I., Chernyshenko, S. I. & Hutchins, N. 2013 Estimating wall-shear-stress fluctuations given an outer region input. J. Fluid Mech. 715, 163–180.Google Scholar
Mathis, R., Marusic, I., Hutchins, N. & Sreenivasan, K. R. 2011b The relationship between the velocity skewness and the amplitude modulation of the small scale by the large scale in turbulent boundary layers. Phys. Fluids 23 (12), 121702.Google Scholar
Mathis, R., Monty, J. P., Hutchins, N. & Marusic, I. 2009b Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes, and channel flows. Phys. Fluids 21 (11), 111703.Google Scholar
Metzger, M., McKeon, B. J. & Holmes, H. 2007 The near-neutral atmospheric surface layer: turbulence and non-stationarity. Phil. Trans. R. Soc. Lond. A 365, 859–876.Google Scholar
Metzger, M. M. & Klewicki, J. C. 2001 A comparative study of near-wall turbulence in high and low Reynolds number boundary layers. Phys. Fluids 13 (3), 692–701.Google Scholar
Metzger, M. M., Klewicki, J. C., Bradshaw, K. L. & Sadr, R. 2001 Scaling the near-wall axial turbulent stress in the zero pressure gradient boundary layer. Phys. Fluids 13 (6), 1819–1821.Google Scholar
Monin, A. S. & Obukhov, A. M. F. 1954 Basic laws of turbulent mixing in the surface layer of the atmosphere. Tr. Akad. Nauk SSSR Geophiz. Inst. 24 (151), 163–187.Google Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.Google Scholar
Nadeem, M., Lee, J. H., Lee, J. & Sung, H. J. 2015 Turbulent boundary layers over sparsely-spaced rod-roughened walls. Intl J. Heat Fluid Flow 56, 16–27.Google Scholar
Ouergli, A. 2002 Hilbert transform from wavelet analysis to extract the envelope of an atmospheric mode: examples. J. Atmos. Ocean. Technol. 19 (7), 1082–1086.Google Scholar
Pathikonda, G. & Christensen, K. T. 2017 Inner–outer interactions in a turbulent boundary layer overlying complex roughness. Phys. Rev. Fluids 2 (4), 044603.Google Scholar
Rajagopalan, S. & Antonia, R. A. 1980 Interaction between large and small scale motions in a two-dimensional turbulent duct flow. Phys. Fluids 23 (6), 1101–1110.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.Google Scholar
Schlatter, P. & Örlü, R. 2010 Quantifying the interaction between large and small scales in wall-bounded turbulent flows: a note of caution. Phys. Fluids 22 (5), 051704.Google Scholar
Spark, E. H. & Dutton, J. A. 1972 Phase angle considerations in the modeling of intermittent turbulence. J. Atmos. Sci. 29 (2), 300–303.Google Scholar
Squire, D. T., Baars, W. J., Hutchins, N. & Marusic, I. 2016 Inner–outer interactions in rough-wall turbulence. J. Turbul. 17 (12), 1159–1178.Google Scholar
Sreenivasan, K. R. 1985 On the fine-scale intermittency of turbulence. J. Fluid Mech. 151, 81–103.Google Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Tracy, C. R., Welch, W. R. & Porter, W. P.1980 Properties of air: a manual for use in biophysical ecology. Tech. Rep. 1. Department of Zoology, University of Wisconsin, Madison.Google Scholar
Tsuji, Y., Marusic, I. & Johansson, A. V. 2016 Amplitude modulation of pressure in turbulent boundary layer. Intl J. Heat Fluid Flow 61, 2–11.Google Scholar
Vallikivi, M.2014 Wall-bounded turbulence at high Reynolds numbers. PhD thesis, Princeton University.Google Scholar
Vallikivi, M., Ganapathisubramani, B. & Smits, A. J. 2015 Spectral scaling in boundary layers and pipes at very high Reynolds numbers. J. Fluid Mech. 771, 303–326.Google Scholar
Wang, G. H. & Zheng, X. J. 2016 Very large scale motions in the atmospheric surface layer: a field investigation. J. Fluid Mech. 802, 464–489.Google Scholar
Wilczak, J. M., Oncley, S. P. & Stage, S. A. 2001 Sonic anemometer tilt correction algorithms. Boundary-Layer Meteorol. 99, 127–150.Google Scholar
Wyngaard, J. C. 1992 Atmospheric turbulence. Annu. Rev. Fluid Mech. 24, 205–233.Google Scholar