Almost extreme waves

Abstract

Numerically computed with high accuracy are periodic travelling waves at the free surface of a two-dimensional, infinitely deep, and constant vorticity flow of an incompressible inviscid fluid, under gravity, without the effects of surface tension. Of particular interest is the angle the fluid surface of an almost extreme wave makes with the horizontal. Numerically found are the following. (i) There is a boundary layer where the angle rises sharply from $0^\circ$ at the crest to a local maximum, which converges to $30.3787\ldots ^\circ$, independently of the vorticity, as the amplitude increases towards that of the extreme wave, which displays a corner at the crest with a $30^\circ$ angle. (ii) There is an outer region where the angle descends to $0^\circ$ at the trough for negative vorticity, while it rises to a maximum, greater than $30^\circ$, and then falls sharply to $0^\circ$ at the trough for large positive vorticity. (iii) There is a transition region where the angle oscillates about $30^\circ$, resembling the Gibbs phenomenon. Numerical evidence suggests that the amplitude and frequency of the oscillations become independent of the vorticity as the wave profile approaches the extreme form.

1. Introduction

Stokes (1847, 1880) made significant contributions to periodic travelling waves at the free surface of an incompressible inviscid fluid in two dimensions, under gravity, without the effects of surface tension. In particular, he observed that crests become sharper and troughs flatter as the amplitude increases, and the so-called extreme wave or wave of greatest height displays a $120^\circ$ corner at the crest. Such an extreme wave bears relevance to breaking, whitecapping, and other physical scenarios. When the flow is irrotational (zero vorticity), based on the reformulation of the problem via conformal mapping as Babenko's nonlinear pseudo-differential equation (see (2.16)), impressive progress was achieved analytically (see, for instance, Buffoni, Dancer & Toland 2000a,b) and numerically (see, for instance, Dyachenko, Lushnikov & Korotkevich 2013, 2016; Lushnikov 2016; Lushnikov, Dyachenko & Silantyev 2017).

For zero vorticity, the angle the fluid surface of the extreme wave makes with the horizontal is $30^\circ$ at the crest and $<30^\circ$ at least near the crest (see, for instance, Amick & Fraenkel 1987; McLeod 1987). Krasovskiĭ (1960, 1961) conjectured that the angle of any Stokes wave is $\leq\ 30^\circ$. So it came as a surprise when Longuet-Higgins & Fox (1977) gave analytical and numerical evidence that the angle of an ‘almost’ extreme wave can exceed $30^\circ$ by about $0.37^\circ$ near the crest. Longuet-Higgins & Fox (1978) took matters further and discovered that the wave speed and several other quantities are not monotone functions of the amplitude but, instead, have maxima and minima within a range of the parameter. McLeod (1997) ultimately proved that Krasovskiĭ's conjecture is false. Chandler & Graham (1993) solved numerically Nekrasov's nonlinear integral equation (see (2.19)) to find that the angle of an almost extreme wave rises sharply from $0^\circ$ at the crest to approximately $30.3787^\circ$ in a thin boundary layer, oscillates about $30^\circ$, resembling the Gibbs phenomenon, and falls to $0^\circ$ at the trough after the oscillations die out (see also figure 2).

Most of the existing mathematical treatments of Stokes waves assume that the flow is irrotational, so that the stream function is harmonic inside the fluid. On the other hand, vorticity has profound effects in many circumstances, for instance, for wind waves or waves in a shear flow. Stokes waves in rotational flows have had a major renewal of interest during the past two decades. We refer the interested reader to, for instance, Haziot et al. (2022) and references therein. Constant vorticity is of particular interest because one can adapt the approaches for zero vorticity. Also, it is representative of a wide range of physical scenarios (see, for instance, Teles da Silva & Peregrine (1988, for more discussion)).

For large values of positive constant vorticity, Simmen & Saffman (1985) (see also Teles da Silva & Peregrine 1988, for finite depth) numerically found overhanging profiles and, taking matters further, profiles that intersect themselves tangentially above the trough to enclose a bubble of air. For zero vorticity, by contrast, the wave profile must be the graph of a single-valued function. Here, we distinguish positive vorticity for upstream propagating waves and negative vorticity for downstream (see, for instance, Teles da Silva & Peregrine (1988, for more discussion)). Recently, Dyachenko & Hur (2019b,c) (see also Dyachenko & Hur 2019a) offered persuasive numerical evidence that for any constant vorticity, Stokes waves are ultimately limited by an extreme wave in the (amplitude) $\times$ (wave speed) plane, which in the zero vorticity case displays a $120^\circ$ corner at the crest. See Appendix A for analytical evidence, similar to Stokes (1847, 1880), that for any constant vorticity, an extreme wave displays a $120^\circ$ corner at the crest.

Here, we solve numerically the Babenko equation, modified to accommodate the effects of constant vorticity (see (2.15)), with unprecedentedly high accuracy, to discover a boundary layer and the Gibbs phenomenon near the crest, alongside other properties of almost extreme waves, in great detail. We offer persuasive numerical evidence that for any constant vorticity, the wave speed oscillates as the amplitude increases monotonically towards that of the extreme wave (see figure 1). We predict that

(1.1)\begin{equation} \frac{c_{ext}-c}{(\sqrt{s_{ext}-s})^3}=\alpha\cos\left(\frac{3}{\rm \pi}\,\kappa\log(s_{ext}-s)+\beta\right)+\cdots\quad \text{as $s\to s_{ext}$} \end{equation}

for some constants $\alpha$ and $\beta$, depending on the vorticity, where $c$ denotes the dimensionless wave speed, and $s$ is the steepness, i.e. the dimensionless wave height, with $c_{ext}$ and $s_{ext}$ for the extreme wave, and $\kappa =1.1220\dots$ is the positive root of

(1.2)\begin{equation} \kappa\tanh \kappa=\frac{\rm \pi}{2\sqrt{3}}, \end{equation}

independently of the vorticity. For zero vorticity, see, for instance, Longuet-Higgins & Fox (1977, 1978) for more discussion. Also, we find numerically the following.

1. (i) For any constant vorticity, there is a boundary layer where the angle the fluid surface of an almost extreme wave makes with the horizontal rises sharply from $0^\circ$ at the crest to a (first) local maximum, which converges monotonically to $30.3787\dots ^\circ$ as the steepness increases towards that of the extreme wave, independently of the vorticity; the thickness of the boundary layer is $\propto s_{ ext}-s$ as $s\to s_{ext}$.

2. (ii) There is an outer region where the angle descends monotonically to $0^\circ$ at the trough for zero and negative constant vorticity, while it rises to a maximum ${>}30^\circ$ and then falls sharply to $0^\circ$ at the trough for large positive vorticity.

3. (iii) There is a transition region where the angle oscillates about $30^\circ$, resembling the Gibbs phenomenon, and the number of oscillations increases as $s$ increases towards that of the extreme wave; the first local minimum converges monotonically to $29.9953\dots ^\circ$ as $s\to s_{ext}$, independently of the vorticity. Numerical evidence suggests that the amplitude and frequency of the angle oscillations reach a limit as $s\to s_{ext}$, independent of the vorticity.

See figures 2–6.

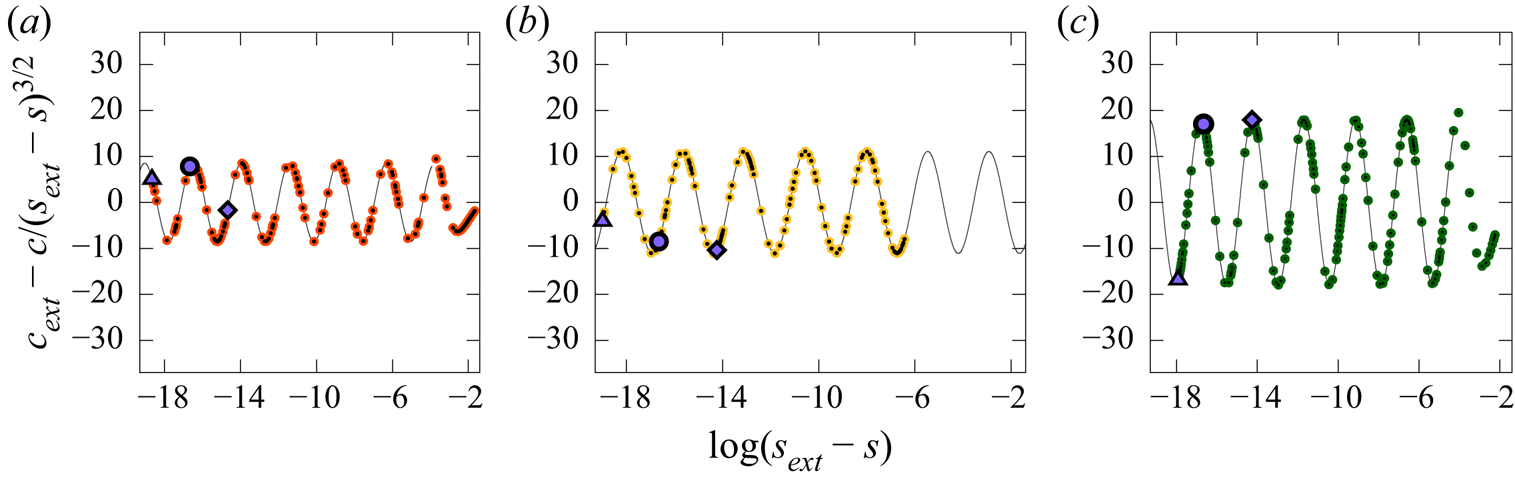
Figure 1. Plots of $(c_{ext}-c)/\sqrt {s_{ext}-s}^3$ versus $\log (s_{ext}-s)$ for: (a) $\omega =0$, red; (b) $\omega =1$, yellow; and (c) $\omega =-1$, green. Dotted curves are the numerical results, and solid curves show cosine curve fitting. See figures 2–4 for solutions corresponding to the circles, triangles and diamonds.

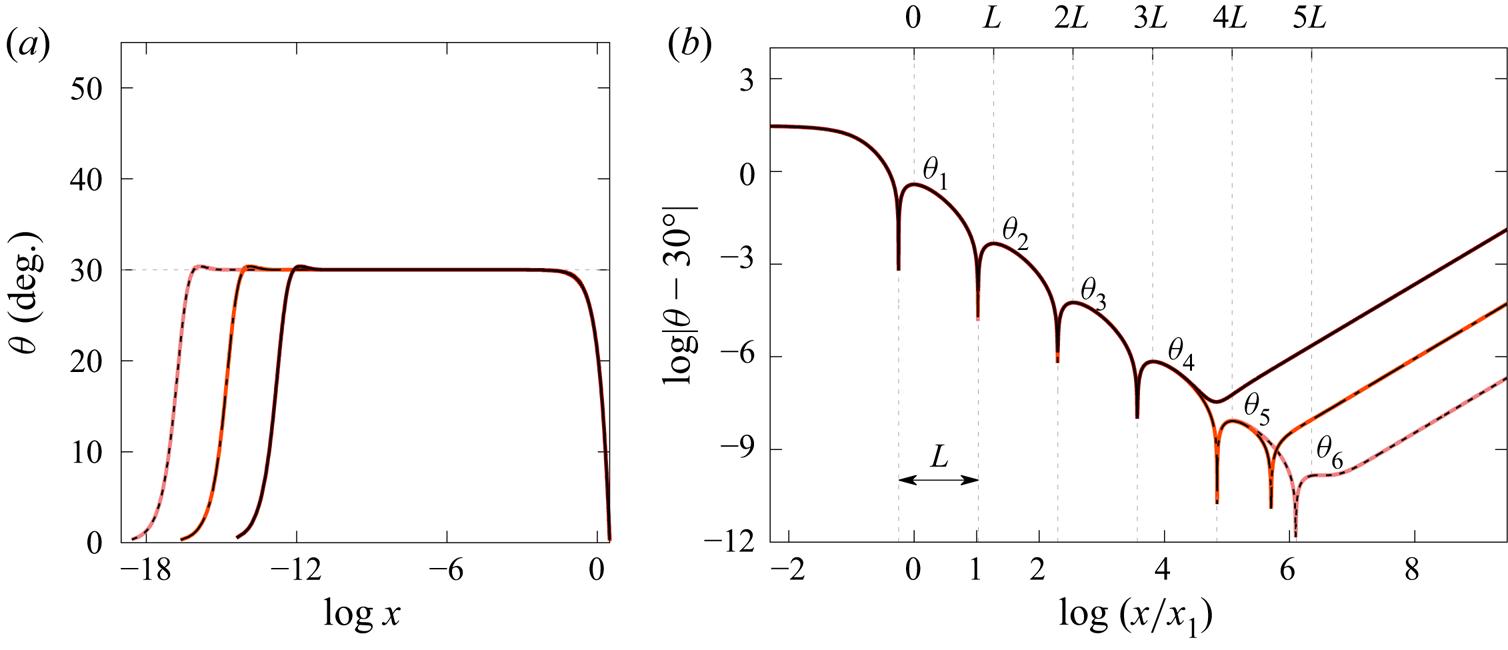
Figure 2. For $\omega =0$: (a) $\theta$ versus $\log x$, $x\in [0,{\rm \pi} ]$, for $s_{ext}-s\approx 10^{-18}$, $10^{-16}$ and $10^{-14}$ for the dotted, dashed and solid curves, respectively; (b) $\log |\theta -30^\circ |$ versus $\log (x/x_1)$ in the Gibbs oscillation region, where $\theta (x_1)=:\theta _1$ is the first local maximum. See table 1 for approximate values of $\theta _j$, $j=1,2,\dots, 6$. We find $L\approx 2.93$ numerically.

Figure 3. For $\omega =1$: (a) $\theta$ versus $\log x$, $x\in [0,{\rm \pi} ]$, for $s_{ext}-s\approx 10^{-19}$, $10^{-16}$ and $10^{-14}$ for the dotted, dashed and solid curves, respectively; (b) $\log |\theta -30^\circ |$ versus $\log (x/x_1)$, where $\theta (x_1)$ is the first local maximum. See table 1 for approximate values of $\theta _1$, $\theta _2$ and $\theta _3$.

Figure 4. For $\omega =-1$, same as in figures 2 and 3. See table 1 for $\theta _1$, $\theta _2$ and $\theta _3$.

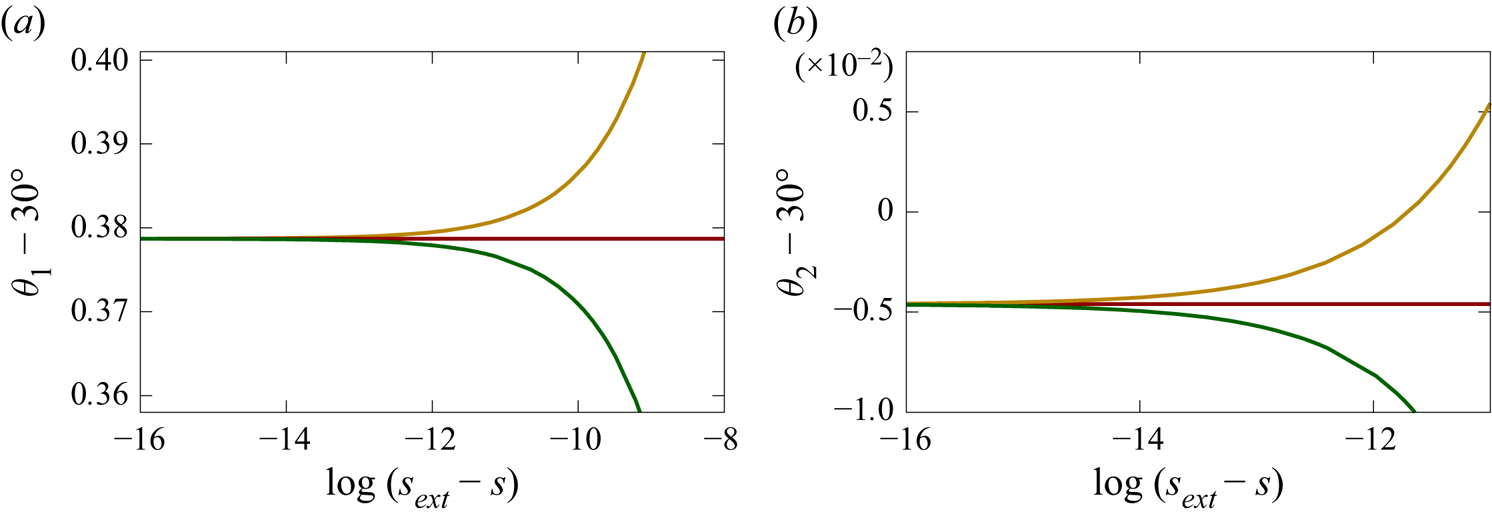
Figure 5. Plots of (a) $\theta _1$ and (b) $\theta _2$ versus $\log (s_{ext}-s)$ for $\omega =0$ (red), $\omega =1$ (yellow) and $\omega =-1$ (green).

Figure 6. (a) Almost extreme waves for $\omega =0$ (red), $\omega =1$ (yellow) and $\omega =-1$ (green), marked by the circles in figure 1, in the $(x,y)$ plane over the interval $x\in [-{\rm \pi},{\rm \pi} ]$. The mean fluid level is at $y=0$. (b) Plot of $\log (x_1)$ versus $\log (s_{ext}-s)$ for $\omega =0$ (red), $\omega =1$ (yellow) and $\omega =-1$ (green). The inset is a close up where $s_{ext}-s$ is $O(10^{-7})$.

It is difficult to resolve accurately the boundary layer and the Gibbs phenomenon because the boundary layer is thin and the angle decreases about two orders of magnitude from one critical value (maximum or minimum) to the next. We solve the modified Babenko equation efficiently using the Newton conjugate residual method, with aid of an auxiliary conformal mapping, to approximate at least 100 decimal digits of the steepness up to $s_{ext}-s\approx 10^{-18}$. See § 3 for details. Our result improves those of Chandler & Graham (1993), Lushnikov et al. (2017), Dyachenko & Hur (2019b,c) and others.

2. Preliminaries

Consider a two-dimensional, infinitely deep, and constant vorticity flow of an incompressible inviscid fluid, under gravity, without the effects of surface tension, and waves at the fluid surface. We assume unit fluid density for simplicity. Suppose for definiteness that in Cartesian coordinates, waves propagate in the $x$ direction and gravity acts in the negative $y$ direction. Suppose that the fluid at time $t$ occupies a region in the $(x,y)$ plane, bounded above by a free surface, say, $y=\eta (x,t)$. Let

(2.1a,b)\begin{equation} D(t)=\{(x,y)\in\mathbb{R}^2: y<\eta(x,t)\} \quad\text{and}\quad S(t)=\{(x,\eta(x,t)):x\in\mathbb{R}\}. \end{equation}

Let $\boldsymbol {u}(x,y,t)$ denote the velocity of the fluid at the point $(x,y)$ and time $t$, and let $P(x,y,t)$ denote the pressure. These satisfy the Euler equations for an incompressible fluid,

(2.2a)\begin{equation} \boldsymbol{u}_t+(\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla})\boldsymbol{u}={-}\boldsymbol{\nabla} P+(0,-g) \quad\text{and}\quad \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{u}=0\quad\text{in $D(t)$}, \end{equation}

where $g$ is the constant acceleration due to gravity. We assume that the vorticity

(2.2b)\begin{equation} \omega:=\boldsymbol{\nabla}\times\boldsymbol{u} \end{equation}

is constant throughout $D(t)$. The kinematic and dynamic boundary conditions are

(2.2c)\begin{equation} \eta_t+\boldsymbol{u}\boldsymbol{\cdot} \boldsymbol{\nabla}(\eta-y)=0 \quad\text{and}\quad P=P_{atm}\quad\text{at $S(t)$}, \end{equation}

where $P_{atm}$ is the constant atmospheric pressure.

Let

(2.3)\begin{equation} \boldsymbol{u}(x,y,t)=(-\omega y,0)+\boldsymbol{\nabla}\phi(x,y,t), \end{equation}

so that

(2.4)\begin{equation} \nabla^2\phi=0\quad\text{in $D(t)$} \end{equation}

by the second equation of (2.2a). Namely, $\phi$ is a velocity potential. We pause to remark that for non-constant vorticity, such a velocity potential is no longer viable to use. Substituting (2.3) into the first equation of (2.2a) and recalling the second equation of (2.2c), after some algebra we arrive at

(2.5)\begin{equation} \phi_t+\tfrac12\,|\boldsymbol{\nabla}\phi|^2-\omega y\phi_x+\omega\psi+P-P_{atm}+gy=B(t)\quad\text{in $D(t)$}, \end{equation}

where $\psi$ is a harmonic conjugate of $\phi$, and $B$ is an arbitrary function. Since $\phi$ and $\psi$ are defined up to addition by functions of $t$, we may assume without loss of generality that

(2.6)\begin{equation} \phi,\psi\rightarrow0\quad\text{as $y\rightarrow-\infty$}\quad\text{uniformly for $x$} \end{equation}

for all time.

We restrict attention to travelling wave solutions to (2.2) and (2.6). That is, $D$, $\phi$ and $\psi$ are stationary in a frame of reference moving with a constant velocity. Let

(2.7a,b)\begin{align} D=\{(x(u,v),y(u,v)): u\in\mathbb{R}~\text{and}~v<0\} \quad\text{and}\quad S=\{(x(u,0),y(u,0)):u\in\mathbb{R}\}, \end{align}

and (2.2) and (2.6) become

(2.8)\begin{equation} \left\{\begin{aligned} & \nabla^2\phi, \nabla^2\psi=0 & & \text{in $D$}, \\ & (\phi_x-\omega y-c)y_u=\phi_yx_u & & \text{at $S$},\\ & \tfrac12(\phi_x+\omega y-c)^2+\tfrac12\phi_y^2+gy=B & & \text{at $S$},\\ & \phi,\psi\to0 & & \text{as $y\to-\infty$}\quad\text{uniformly for $x$}, \end{aligned}\right. \end{equation}

for some $c\neq 0$, the wave speed, where $B$ is an arbitrary constant. After the change of variables

(2.9)\begin{equation} y\mapsto y+y_0\quad\text{and}\quad c\mapsto c-\omega y_0\quad\text{for some $y_0\in\mathbb{R}$}, \end{equation}

we may assume that $B=0$. Additionally, we assume that $D$ and $\psi$ are periodic in the horizontal direction and symmetric about the vertical lines below the crest and trough. We assume without loss of generality that the period is $2{\rm \pi}$.

2.1. The modified Babenko equation

Proceeding as in Dyachenko & Hur (2019b,c) and others, we reformulate (2.8) in ‘conformal coordinates’. In what follows, we identify $\mathbb {R}^2$ with $\mathbb {C}$ whenever it is convenient to do so.

Suppose that

(2.10)\begin{equation} (x+\mathrm{i} y)(u+\mathrm{i} v) \end{equation}

maps $\mathbb {C}_-:=\{u+\mathrm {i} v\in \mathbb {C}:v<0\}$ conformally to $D$ and that

(2.11)\begin{equation} (x+\mathrm{i} y)(u+\mathrm{i} v)-(u+\mathrm{i} v) \end{equation}

is $2{\rm \pi}$ periodic in $u$ and $(x+\mathrm {i} y)(u+\mathrm {i} v)-(u+\mathrm {i} v)\to 0$ as $v\to -\infty$ uniformly for $u$. Suppose that (2.10) extends to map $\overline {\mathbb {C}_-}$ continuously to $D\cup S$. We recall from the theory of Fourier series that

(2.12)\begin{equation} (x+\mathrm{i} y)(u+\mathrm{i} 0)=u+((\mathcal{H}+\mathrm{i})y)(u+\mathrm{i}0), \end{equation}

where $\mathcal {H}$ denotes the periodic Hilbert transform, defined as

(2.13)\begin{equation} \mathcal{H}\,{\rm e}^{\mathrm{i} ku}={-}\mathrm{i}\,\text{sgn}(k)\,{\rm e}^{\mathrm{i} ku},\quad k\in\mathbb{Z}. \end{equation}

Abusing notation, let $(\phi +\mathrm {i}\psi )(u+\mathrm {i} v)=(\phi +\mathrm {i}\psi )((x+\mathrm {i} y)(u+\mathrm {i} v))$, and we recall from the theory of Fourier series that

(2.14)\begin{equation} (\phi+\mathrm{i}\psi)(u+\mathrm{i}0)=((1-\mathrm{i}\mathcal{H})\phi)(u+\mathrm{i}0). \end{equation}

Substituting (2.12) and (2.14) into (2.8), after some algebra, we arrive at

(2.15)\begin{equation} c^2\mathcal{H}y_u-(g+\omega c)y=g(y\mathcal{H}y_u+\mathcal{H}(yy_u)) +\tfrac12\omega^2(y^2+\mathcal{H}(y^2y_u)+y^2\mathcal{H}y_u-2y\mathcal{H}(yy_u)). \end{equation}

When $\omega =0$ (zero vorticity), (2.15) becomes

(2.16)\begin{equation} c^2\mathcal{H}y_u-gy=g(y\mathcal{H}y_u+\mathcal{H}(yy_u)), \end{equation}

namely the Babenko equation (Babenko 1987).

A solution of (2.15) gives rise to a solution of (2.8), provided that

(2.17a)\begin{equation} \text{$u\mapsto u+\mathcal{H}\,y(u)+\mathrm{i}\,y(u)$ is injective for all $u\in\mathbb{R}$}\end{equation}

and

(2.17b)\begin{equation} \text{$(1+\mathcal{H}\,y_u(u))^2+y_u(u)^2\neq 0 \quad $for all $\,u \in\mathbb{R}$}.\end{equation}

We pause to remark that (2.17a) expresses that the fluid surface does not intersect itself, and (2.17b) ensures that (2.10) is well-defined throughout $\overline {\mathbb {C}_-}$. Dyachenko & Hur (2019b,c) offered numerical evidence that the solutions of (2.15) can be found even though (2.17a) fails to hold, but such solutions are ‘physically unrealistic’ because the fluid surface intersects itself and the fluid flow becomes multi-valued. Recently, Hur & Wheeler (2022) gave a rigorous proof that there exists a ‘touching’ wave, whose profile intersects itself tangentially at one point above the trough to enclose a bubble of air.

If (2.17b) fails to hold, on the other hand, then there would be a stagnation point at the fluid surface, where the velocity of the fluid particle vanishes in the moving frame of reference. Numerical evidence supports that for any constant vorticity, the solutions of (2.15) would be limited ultimately by an extreme wave in the (amplitude) $\times$ (wave speed) plane, which would display a corner at the crest. In Appendix A, we give analytical evidence, similar to (Stokes 1847, 1880), that for any value of $\omega$, the angle at the crest would be $120^\circ$. Here we are interested in ‘almost’ extreme waves.

2.2. The Nekrasov equation

Let

(2.18)\begin{equation} \theta=\arctan\left(\frac{y_u}{x_u}\right) \end{equation}

denote the angle that the fluid surface makes with the horizontal at the point $(x(u),y(u))$, $u\in [-{\rm \pi},{\rm \pi} ]$. When $\omega =0$,

(2.19)\begin{equation} \theta(u)=\frac{1}{3{\rm \pi}}\int^{\rm \pi}_0 \log\left|\frac{\sin\tfrac12(u+u')}{\sin\tfrac12(u-u')}\right| \frac{\sin\theta(u')}{\mu+\displaystyle\int\nolimits^{u'}_0\sin\theta}\,{\rm d}u', \end{equation}

where

(2.20)\begin{equation} \mu=\frac{1}{3gc}\left(\sqrt{c^2-2g\,y(0)}\right)^3, \end{equation}

namely the Nekrasov equation (Nekrasov 1921). We refer the interested reader to, for instance, Buffoni et al. (2000a,b) for details. Throughout, we use subscripts for partial derivatives and primes for variables of integration. We pause to remark that $\sqrt {c^2-2g\,y(0)}$ is the speed of the fluid particle at the crest.

Amick, Fraenkel & Toland (1982) and others proved that for $\mu =0$, there exists an extreme wave and $|\theta (u)|\to 30^\circ$ as $u\to 0$; Plotnikov & Toland (2004) proved that $|\theta (u)|$ decreases monotonically over the interval $u\in [0,{\rm \pi} ]$, so that $\sup _{u\in [0,{\rm \pi} ]}|\theta (u)|=30^\circ$. For $\mu \ll 1$, on the other hand, McLeod (1997) proved that $\sup _{u\in [0,{\rm \pi} ]}|\theta (u)|>30^\circ$.

For $\mu$ sufficiently small, Chandler & Graham (1993) solved numerically (2.19) to find that: the angle increases from $0^\circ$ at the crest to a maximum ${\approx } 30.3787^\circ$ in a boundary layer of size $O(\mu )$; the angle then oscillates about $30^\circ$, and the number of oscillations increases as $\mu \to 0$; and the angle decreases to $0^\circ$ outside the oscillation region. Here, we solve numerically (2.16), with unprecedentedly high accuracy, to improve the result of Chandler & Graham (1993), and take matters further to include the effects of constant vorticity.

3. Methods

We write (2.15) abstractly as

(3.1)\begin{equation} \mathcal{G}(y,c)=0, \end{equation}

and solve it iteratively by means of Newton's method. Let

(3.2)\begin{equation} y^{(n+1)}=y^{(n)}+\delta y^{(n)},\quad n=0,1,2,\dots, \end{equation}

where $y^{(0)}$ is an initial guess and

(3.3)\begin{equation} \delta\,\mathcal{G}(y^{(n)},c)\,\delta y^{(n)}={-}\mathcal{G}(y^{(n)},c), \end{equation}

where $\delta \mathcal {G}(y^{(n)},c)$ linearizes $\mathcal {G}(y,c)$ with respect to $y$, and evaluates $y=y^{(n)}$. We solve (3.3) numerically using Krylov subspace methods. We approximate $y^{(n)}$ and $\delta y^{(n)}$ using a discrete cosine transform, and compute efficiently using a fast Fourier transform. We treat $\mathcal {H}y^{(n)}$ and others likewise. Once we obtain a convergent solution, we continue it in $c$. We refer the interested reader to Yang (2010), for instance, for details.

3.1. Auxiliary conformal mapping

In what follows, we employ the notation $z=x+\mathrm {i} y$ and $w=u+\mathrm {i} v$.

In the $\omega =0$ (zero vorticity) case, Dyachenko et al. (2013, 2016) and others gave numerical evidence that an analytic continuation of (2.10) to $\mathbb {C}$ has branch points at $w=2n{\rm \pi} +\mathrm {i} v_0$, $n\in \mathbb {Z}$, for some $v_0>0$. Also,

(3.4)\begin{equation} z(w)-w=\sum_{k\in\mathbb{Z},k\leqslant0} \hat{z}(k)\,{\rm e}^{{\rm i}kw},\quad \text{where $|\hat{z}(k)|\propto \exp({-}v_0|k|)$}\quad\text{as $|k|\rightarrow\infty$}, \end{equation}

for $v_0$ sufficiently small. Recall that $v_0\rightarrow 0$ as the wave profile approaches the extreme form. This presents enormous technical challenges for numerical computation. Nevertheless, Dyachenko et al. (2016) used $2^{27}\ (\approx 1.3\times 10^{8})$ Fourier coefficients to approximate $32$ decimal digits of the steepness for $v_0\approx 10^{-7}$.

To achieve higher accuracy, Lushnikov et al. (2017) introduced

(3.5a,b)\begin{equation} w=2\arctan\left(\varepsilon\tan\frac12\zeta\right)\quad\text{and}\quad \zeta=2\arctan\left(\frac{1}{\varepsilon}\tan\frac12w\right) \end{equation}

for some $\varepsilon >0$, to be determined in the course of numerical experiment. Note that (3.5) maps $\mathbb {C}_-$ conformally to $\mathbb {C}_-$, and $\mathbb {R}+\mathrm {i}0$ to $\mathbb {R}+\mathrm {i}0$, and (3.5) is $2{\rm \pi}$ periodic in the real variables. In the $\omega =0$ case, therefore, one may solve (see (2.16))

(3.6)\begin{equation} c^2\mathcal{H}y_\zeta-gu_\zeta y=g(y\mathcal{H}y_\zeta+\mathcal{H}(yy_\zeta)),\quad \zeta\in\mathbb{R}, \end{equation}

where $\mathcal {H}$ is the periodic Hilbert transform in the $\zeta$ variable, and $u_\zeta$ is the Jacobian of (3.5). Since $u\approx \varepsilon \zeta$, $\zeta \in \mathbb {R}$, about $\zeta =0$ for $\varepsilon \ll 1$, (3.5) maps uniform grid points of $\zeta$ to non-uniform grid points of $u$, concentrating the points about $u=0$. Also, (3.5b) maps $\mathrm {i} v_0$ to, say, ${\rm i}\zeta _0=\mathrm {i} v_0/\varepsilon +O((v_0/\varepsilon )^3)$ for $v_0/\varepsilon \ll 1$, so that

(3.7)\begin{align} z(w(\zeta))-w(\zeta)=\sum_{k\in\mathbb{Z},k\leqslant0}\hat{z}(k)\,{\rm e}^{{\rm i}k\zeta},\quad \text{where $|\hat{z}(k)|\propto \exp\left(-\frac{v_0}{\varepsilon}|k|\right)$}\quad\text{as $|k|\to\infty$} \end{align}

for $v_0/\varepsilon \ll 1$, provided that there are no singularities of (3.5a) closer to $\mathbb {C}_-$ than $i\zeta _0$. A straightforward calculation reveals that (3.5a) has branch points at $\zeta =2n{\rm \pi} \pm 2\arctan (\mathrm {i}/ \varepsilon )=(2n\pm 1){\rm \pi} \pm 2\mathrm {i}\varepsilon +O(\mathrm {i}\varepsilon ^3)$, $n\in \mathbb {Z}$, for $\varepsilon \ll 1$. One may therefore choose $\varepsilon \approx \sqrt {\tfrac 12v_0}$, $v_0\ll 1$, so that

(3.8)\begin{align} z(w(\zeta))-w(\zeta)=\sum_{k\in\mathbb{Z},k\leqslant0}\hat{z}(k)\,{\rm e}^{{\rm i}k\zeta},\quad\text{where $|\hat{z}(k)|\propto \exp(-\sqrt{2v_0}|k|)$}\quad\text{as $|k|\to\infty$}. \end{align}

This improves numerical convergence. For instance, Lushnikov et al. (2017) used about $10^4$ Fourier coefficients to obtain the same result as Dyachenko et al. (2013, 2016) did with ${\approx }10^8$ Fourier coefficients.

Here, we take matters further and resort to

(3.9)\begin{equation} w=2\,\mathrm{am}\left({K}(\sqrt{m})\,\frac{\zeta+{\rm \pi}}{\rm \pi},\sqrt{m}\right)-{\rm \pi} \end{equation}

for some $m$ in the range $(0,1)$, where $\mathrm {am}$ denotes the Jacobi amplitude; that is, for the elliptic parameter $m$ (rather than the elliptic modulus $k$ such that $m=k^2$),

(3.10a,b)\begin{align} \varphi=\mathrm{am}(u,\sqrt{m})=F^{{-}1}(u,\sqrt{m}),\quad\text{and}\quad u=F(\varphi,\sqrt{m})=\int_0^\varphi\frac{{\rm d}\varphi'}{\sqrt{1-m\sin^2\varphi}} \end{align}

is the incomplete elliptic integral of the first kind;

(3.11)\begin{equation} {K}(\sqrt{m})=\int_0^1\frac{{\rm d}t}{\sqrt{(1-t^2)(1-mt^2)}} \end{equation}

is the complete elliptic integral of the first kind. We refer the interested reader, for instance, to Hale & Tee (2009) for more discussion. We calculate

(3.12)\begin{equation} \zeta=\frac{\rm \pi}{{K}(\sqrt{m})}\,F\left(\frac12\,w+{\rm \pi},\sqrt{m}\right)-{\rm \pi}. \end{equation}

Note that (3.9) maps $\{\zeta \in \mathbb {C}:-{\rm \pi} ({{K}'(\sqrt {m})}/{{K}(\sqrt {m})})<\text {Im}\,\zeta <0\}$ conformally to $\mathbb {C}_-$, and $\mathbb {R}+\mathrm {i}0$ to $\mathbb {R}+\mathrm {i}0$, where ${K}'(\sqrt {m})={K}(\sqrt {1-m})$, and (3.9) and (3.12) are $2{\rm \pi}$ periodic in the real variables. Note that (3.9) maps $\mathrm {i} \zeta$, $\zeta >0$, to $\mathrm {i} v$, where

(3.13a,b)\begin{equation} \zeta={\rm \pi}\frac{{K}'(\sqrt{m})}{{K}(\sqrt{m})}\quad\text{and}\quad m=1-\tanh^2\left(\frac12v\right)=\mathrm{sech}^2\left(\frac12v\right). \end{equation}

Note that (3.9) maps $[0,\mathrm {i} \zeta ]$, $\zeta >0$, to $[0,\mathrm {i} v]$, where $\zeta$ and $v$ are in (3.13a,b). Also note that (3.9) maps $[-{\rm \pi} +\mathrm {i}\zeta,0+\mathrm {i}\zeta ]$ and $[0+\mathrm {i}\zeta,{\rm \pi} +\mathrm {i}\zeta ]$ to $[\mathrm {i} v,+\mathrm {i}\infty ]$, making a branch cut of (3.9).

A straightforward calculation reveals that

(3.14)\begin{equation} \zeta_w(\zeta)=\frac{\rm \pi}{2}\,\frac{\mathrm{dn}\left(\dfrac1{\rm \pi}\,{K}(\sqrt{m})\,\zeta,\sqrt{m}\right)}{\sqrt{1-m}\,{K}(\sqrt{m})}, \end{equation}

where $\mathrm {dn}$ is a Jacobi elliptic function, defined as $\mathrm {dn}(u,\sqrt {m})=\sqrt {1-m\sin ^2(\mathrm {am}(u,\sqrt {m}))}$. Recall that $\mathrm {dn}({\cdot },\sqrt {m})$ has periods $2\,{K}(\sqrt {m})$ and $4\mathrm {i}\,{K}'(\sqrt {m})$, zeros at $(2n+1){K}+(2n'+1)\mathrm {i}{K}'$, and simple poles at $2n{K}+2n'\mathrm {i}{K}'$ for any $n,n'\in \mathbb {Z}$, so that

(3.15)\begin{equation} \zeta_w(\zeta)=0\quad\text{at}\ \zeta={\pm}{\rm \pi}+(2n+1)\mathrm{i}{\rm \pi}\,\frac{{K}'(\sqrt{m})}{{K}(\sqrt{m})}, \quad n\in\mathbb{Z}, \end{equation}

and

(3.16)\begin{equation} \zeta_w(\zeta)\to\infty\quad\text{at}\ \zeta=0+2n\mathrm{i}{\rm \pi}\,\frac{{K}'(\sqrt{m})}{{K}(\sqrt{m})},\quad n\in\mathbb{Z}. \end{equation}

For $v_0>0$ and sufficiently small, where $\mathrm {i} v_0$ is the closest singularity of (2.10) to $\mathbb {C}_-$, therefore we choose

(3.17)\begin{equation} m=1-\tanh^2\left(\tfrac12v_0\right)=\mathrm{sech}^2\left(\tfrac12v_0\right), \end{equation}

so that (3.9) maps $[-{\rm \pi} +\mathrm {i} \zeta _0,0+\mathrm {i} \zeta _0]$ and $[0+\mathrm {i} \zeta _0,{\rm \pi} +\mathrm {i} \zeta _0]$ to $[\mathrm {i} v_0,+\mathrm {i}\infty ]$, that is, the branch cut of (3.9) to the branch cut of (2.10), where

(3.18)\begin{equation} \zeta_0={\rm \pi}\,\frac{{K}'(\sqrt{m})}{{K}(\sqrt{m})}\approx \frac{{\rm \pi}^2}{2}\,\frac{1}{\log(8/v_0)} \quad\text{for $v_0\ll1$}. \end{equation}

Correspondingly,

(3.19)\begin{align} z(w(\zeta))-w(\zeta)=\sum_{k\in\mathbb{Z},k\leqslant0}\hat{z}(k)\,{\rm e}^{{\rm i}k\zeta},\quad \text{where }|\hat{z}(k)|\propto \exp\left(-\frac{{\rm \pi}^2}{2}\,\frac{|k|}{\log(8/v_0)}\right)\quad\text{as $|k|\to\infty$} \end{align}

for $v_0\ll 1$. This dramatically improves numerical convergence. For instance, for $v_0=10^{-30}$, one would need about $10^{17}$ Fourier coefficients using (3.5) for approximating a solution with $10^{-36}$ error, whereas about $10^3$ Fourier coefficients would suffice for (3.9).

3.2. Method for non-zero vorticity: conjugate gradient versus conjugate residual

Since

(3.20)\begin{align} \delta\,\mathcal{G}(y,c)\,\delta y&=c^2\,\mathcal{H}(\delta y)_u-(g+c\omega)\,\delta y -g(\delta y\,\mathcal{H}y_u+y\,\mathcal{H}(\delta y)_u+\mathcal{H}(y\,\delta y)_u) \nonumber\\ &\quad -\tfrac12\omega^2(2y\,\delta y+\mathcal{H}(y^2\,\delta y)_u-[2y\,\delta y,y]+[y^2,\delta y] \end{align}

is self-adjoint, where $[f_1,f_2]=f_1\mathcal {H}f_2-f_2\mathcal {H}f_1$, Dyachenko & Hur (2019b) employed the conjugate gradient (CG) method (see, for instance, Yang 2010) to solve numerically (3.3). For any value of $\omega$, the CG method converges within a range of the parameters, although $\delta \,\mathcal {G}(y,c)$ is not positive definite, but the method breaks down as the wave profile approaches the extreme form. Even when the method converges, the solution error is not a monotonically decreasing function of the number of iterations for almost extreme waves.

Here, we resort to Krylov subspace methods for symmetric indefinite systems, particularly, minimal residual (MINRES) methods. MINRES minimizes the $L^2$-norm of the residual and does not suffer from breakdown. See, for instance, Paige & Saunders (1975) for more discussion. Indeed, replacing the CG method by the conjugate residual (CR) method works well for any value of $\omega$ for almost extreme waves, and the solution error is monotonically decreasing.

We require the truncation error $|\widehat {y^{(n)}}(N/2)|\lesssim 10^{-36}$, where $N$ is the number of Fourier coefficients or, alternatively, the number of uniform grid points in the $\zeta$ variable, and the residual $\|\mathcal {G}(y^{(n)}, c)\|_{L^2}\lesssim 10^{-43}$, to approximate $100$ decimal digits of the steepness for $s_{ext}-s$ up to $10^{-19}$, where $s$ is the steepness, with $s_{ext}$ for the extreme wave.

The wave speed oscillations become exponentially small along the solution curve as $s$ increases monotonically to $s_{ext}$ (see figure 1) and our numerical computation must use arbitrary-precision floating-point numbers. We use the GNU MPFR library for variable precision numbers (see, for instance, Fousse et al. 2007), increasing the number of bits per floating point number as $s\to s_{ext}$.

3.3. Method for zero vorticity

For $\omega =0$, alternatively, we solve (3.3) non-iteratively because solving a $4096\times 4096$ linear system would suffice to approximate $100$ decimal digits of the steepness for $s_{ext}-s$ up to $10^{-18}$. The solution error decreases quadratically, that is, the number of significant digits in the numerical solution increases by a factor of $2$ in each Newton iteration so long as the method converges.

4. Results

In the $\omega =0$ (zero vorticity) case, Dyachenko et al. (2016), Lushnikov et al. (2017) and others gave numerical evidence that the wave speed converges oscillatorily to that of the extreme wave as the steepness increases monotonically towards that of the extreme wave. The wave speed decreases about two orders of magnitude from one critical value (maximum or minimum) to the next, though, and it is difficult to resolve accurately such wave speed oscillations. Nevertheless, Lushnikov et al. (2017) resolved about $3.5$ oscillations, predicting that

(4.1)\begin{equation} \frac{c_{ext}-c}{\sqrt{s_{ext}-s}^3} =\alpha\cos\left(\frac{\rm \pi}{3}\,\kappa\log(s_{ ext}-s)+\beta\right)+\cdots \quad\text{as $s\to s_{ext}$} \end{equation}

for some constants $\alpha$ and $\beta$, where $\kappa =1.1220\dots$ is the positive root of

(4.2)\begin{equation} \kappa\tanh \kappa=\frac{\rm \pi}{2\sqrt{3}}. \end{equation}

Throughout, we take $g=1$, $c$ denotes the wave speed, and $s$ denotes the steepness – the crest-to-trough vertical distance divided by the period – with $c_{ext}$ and $s_{ext}$ for the extreme wave. See also Longuet-Higgins & Fox (1978) for more discussion.

Figure 1(a) shows $(c_{ext}-c)/\sqrt {s_{ext}-s}^3$ versus $\log (s_{ext}-s)$ for $\omega =0$ for $s_{ext}-s$ up to $10^{-18}$, and compares the result with (4.1), where $c_{ext}$, $s_{ext}$ and $\alpha$, $\beta$ are determined from the numerics. We exploit an auxiliary conformal mapping (see (3.9)) to improve the result of Lushnikov et al. (2017) and others, resolving about $6.5$ oscillations. We report $c_{ext}=1.0922850485\dots$ and $s_{ext}=0.1410634839\dots$.

Figures 1(b,c) show $(c_{ext}-c)/\sqrt {s_{ext}-s}^3$ versus $\log (s_{ext}-s)$ for $\omega =1$ and $-1$ for $s_{ext}-s$ up to $10^{-19}$, and compare the numerical results with (4.1), discovering that $\alpha$ and $\beta$ depend on $\omega$ but, interestingly, $\kappa$ does not. We predict that for any constant vorticity, the wave speed oscillates as $c\to c_{ext}$ while $s\to s_{ext}$ monotonically, and the frequency of the wave speed oscillations is independent of the vorticity. We report $c_{ext}=2.2683602961\dots$ and $s_{ext}=0.4431049878\dots$ for $\omega =1$, and $c_{ext}=0.6710639577\dots$ and $s_{ext}=0.0492991750\dots$ for $\omega =-1$.

In what follows, by the angle, abusing notation, denoted $\theta$ we mean the angle – measured clockwise – that the fluid surface makes with the horizontal.

We begin by taking $\omega =0$. Figure 2(a) shows the graph of $\theta$ as a function of $x$, over the interval $x\in [0,{\rm \pi} ]$, for an almost extreme wave for which $s_{ext}-s\approx 10^{-18}$, and compares the result with two other almost extreme waves, for which $s_{ext}-s\approx 10^{-16}$ and $10^{-14}$. Note that the horizontal axis is logarithmic. The three almost extreme waves are marked by the triangle, circle and diamond in figure 1(a). We report $c=1.0922850485\dots$ for the dotted, dashed and solid curves, agreeing on at least $20$ decimal digits.

We find numerically a boundary layer where $\theta$ rises sharply from $\theta (0)=0^\circ$ to a (first) local maximum $\theta (x_1)=:\theta _1$, and an outer region where $\theta$ falls to $\theta ({\rm \pi} )=0^\circ$. We report $s_{ext}-s=1.3777\ldots \times 10^{-18}$ and $x_1=1.4095\ldots \times 10^{-16}$ (dotted), $s_{ext}-s=1.3604\ldots \times 10^{-16}$ and $x_1=1.3918\ldots \times 10^{-14}$ (dashed), and $s_{ext}-s=1.3460\ldots \times 10^{-14}$ and $x_1= 1.3771\ldots \times 10^{-12}$ (solid), predicting that $x_1\approx 102.3(s_{ext}-s)$ as $s \to s_{ext}$. Also, we find numerically a transition region where $\theta$ oscillates about $30^\circ$, resembling Gibbs phenomenon, although not visible in the scale. Our result agrees with Chandler & Graham (1993) and others.

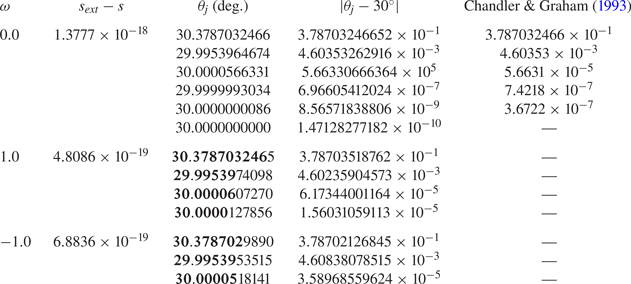
Figure 2(b) shows the Gibbs oscillations in the logarithmic scale. We resolve numerically six critical values, denoted $\theta _j:=\theta (x_j)$, $j=1,2,\dots,6$, and $0< x_1< x_2<\cdots < x_6<{\rm \pi}$, while observing that the number of oscillations increases as $s$ increases towards $s_{ext}$. Table 1 gives approximate critical values for $s_{ext}-s=1.3777\ldots \times 10^{-18}$, or equivalently, $\mu = 2.1978\ldots \times 10^{-26}$ (see (2.20)), and compares the result with five critical values computed by Chandler & Graham (1993) for $\mu =10^{-18}$. Recall that $\mu \to 0$ as $s\to s_{ext}$. We predict that

(4.3)\begin{equation} \theta_1\to 30.3787032466\dots^\circ\quad\text{and}\quad \theta_2 \to 29.9953964674\dots^\circ\quad\text{as $s\to s_{ext}$}. \end{equation}

Also, numerical evidence suggests that

(4.4)\begin{align} \frac{|\theta_{j+1}-30^\circ|}{|\theta_j-30^\circ|}\approx 1.22\times 10^{{-}2} \quad\text{and}\quad \frac{x_{j+1}}{x_j}\approx 18.73\quad \text{for $s_{ext}-s\ll1$}, \quad j=1,2,\dots, \end{align}

or equivalently, $L:=\log (x_{j+1}/x_1)-\log (x_j/x_1)\approx 2.93$ as $s \to s_{ext}$, independently of $j$. In particular, $x_j\to 0$ as $s\to s_{ext}$ for all $j$.

Table 1. Approximate values of $\theta _j$ for $s_{ext}-s\ll 1$ for $\omega =0$, $1$ and $-1$, and in the $\omega =0$ case, comparison with Chandler & Graham (1993). Digits in bold agree up to rounding across numerical computation and also the result for $\omega =0$.

We turn our attention to $\omega =1$. Figure 3 shows $\theta$ versus $x$, $x\in [0,{\rm \pi} ]$, in the logarithmic scale, for three almost extreme waves, marked by the triangle, circle and diamond in figure 1(b). We report $c=2.2683602961\dots$ and $s_{ext}-s\approx 10^{-19}$, $10^{-16}$ and $10^{-14}$ for the dotted, dashed and solid curves, respectively. Numerically found are a boundary layer where $\theta$ rises sharply from $\theta (0)=0^\circ$ to a first local maximum $\theta (x_1)=:\theta _1$, where $x_1\approx 102.4(s_{ext}-s)$ as $s \to s_{ext}$, and a Gibbs oscillation region, the same as for the $\omega =0$ case. We resolve numerically up to the second local maximum angle for $s_{ext}-s\approx 10^{-19}$, while observing that higher-order local maxima and minima set in for $s$ closer to $s_{ext}$, compared with the $\omega =0$ case. See table 1 for approximate critical values for $s_{ext}-s=4.8086\ldots \times 10^{-19}$. We predict that $\theta _1\to 30.378703256\dots ^\circ$ and $\theta _2\to 29.99539\dots ^\circ$ as $s\to s_{ext}$, as in the $\omega =0$ case (see (4.3)). Also, we predict that $L:=\log (x_{j+1}/x_1)-\log (x_j/x_1)\approx 2.93$ as $s\to s_{ext}$, independently of $j$, as in the $\omega =0$ case (see (4.4)). But an important difference is that in the outer region, $\theta$ rises to a maximum $52.1426155193\dots ^\circ$ and then falls sharply to $\theta ({\rm \pi} )=0^\circ$. See figure 3(a).

Last but not least, in the $\omega =-1$ case, figure 4 shows $\theta$ for $s_{ext}-s\approx 10^{-19}$, $10^{-16}$ and $10^{-14}$, corresponding to the triangle, circle and diamond in figure 1(c), respectively. We report $c =0.6710639577\dots$. The result is the same as in the $\omega =0$ case, but critical values of the angle set in for $s_{ext}-s$ smaller compared with the $\omega =0$ case.

Figure 5 shows that the first local maximum angle in the oscillation region converges monotonically to $30.3787\dots ^\circ$, and the first local minimum converges monotonically to $29.9953\dots ^\circ$ as $s\to s_{ext}$, independently of the constant vorticity. We predict that higher-order local maxima and minima converge monotonically as $s\to s_{ext}$, independently of the vorticity. By contrast, the wave speed and several other quantities are not monotone functions of the steepness (see figure 1).

Figure 6(a) shows the profiles of almost extreme waves for $\omega =0$, $1$ and $-1$ in the $(x,y)$ plane over one period. We report

• $s=0.141063483979936080716$ ($s/s_{ext}=0.99999999999999999023$) for $\omega =0$,

• $s=0.44310498782481126969$ ($s/s_{ext}=0.99999999999999999831$) for $\omega =1$,

• $s=0.049299175088933178$ ($s/s_{ext}=0.999999999999999738$) for $\omega =-1$.

Figure 6(b) shows $x_1$ as a function of $s_{ext}-s$, in the logarithmic scale, for $\omega =0$, $1$ and $-1$. Numerical evidence is clear that the thickness of the boundary layer is $\propto s_{ext}-s$ as $s\to s_{ext}$, independently of the constant vorticity.

5. Conclusions

For any constant vorticity, for the steepness sufficiently close to that of the extreme wave, we find numerically the following.

1. (i) There is a boundary layer where the angle the fluid surface of such an almost extreme wave makes with the horizontal rises sharply from $0^\circ$ at the crest to a first local maximum, which converges monotonically to $30.3787\dots ^\circ$ as $s\to s_{ext}$, independently of the vorticity; the thickness of the boundary layer is $\approx 102(s_{ext}-s)$, independently of the vorticity.

2. (ii) There is an outer region where the angle descends to $0^\circ$ at the trough for zero and negative vorticity, while it rises to a maximum ${>}30^\circ$ and then falls sharply to $0^\circ$ at the trough for large positive vorticity.

3. (iii) There is a transition region, where the angle oscillates about $30^\circ$, bearing resemblance to the Gibbs phenomenon; the number of oscillations increases as $s\to s_{ext}$; the first local minimum angle converges monotonically to $29.9953\dots ^\circ$ as $s \to s_{ext}$, independently of the vorticity.

Let $\theta _j=\theta (x_j)$ denote the $j$th critical value of the angle in the oscillation region, where $0< x_1< x_2<\dots < x_j<\dots <{\rm \pi}$. Numerical evidence suggests that $\theta _j$ converges monotonically to a limit, while $|\theta _{j+1}-30^\circ |/|\theta _j-30^\circ |\to 1.22\times 10^{-2}$ as $s\to s_{ext}$, for each $j$, independently of the vorticity. Also, $x_j\to 0$ while $x_{j+1}/x_j \to 18.72\dots$ as $s\to s_{ext}$, for each $j$, independently of the vorticity.

Perhaps the angle oscillations have relevance to the singularities of the conformal mapping for the Stokes wave (see (2.10)), where square root branch points in Riemann sheets tend to $w=0$ (corresponding to the crest) in a self-similar manner as the wave profile approaches the extreme form (for more discussion, see, for instance, Dyachenko et al. 2016; Lushnikov 2016).

For zero vorticity, Chandler & Graham (1993) solved the Nekrasov equation (see (2.19)) efficiently to discover a boundary layer and the Gibbs phenomenon near the crest of an almost extreme wave with remarkable accuracy. For non-zero constant vorticity, there is no such integral equation, to the best of the authors’ knowledge, and we instead solve the modified Babenko equation (see (2.15)) with sufficiently high accuracy.