Article contents
Airfoil response to periodic vertical and longitudinal gusts
Published online by Cambridge University Press: 17 January 2024
Abstract
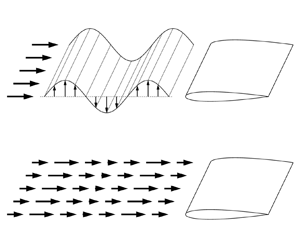
Gust response has consistently been a concern in engineering. Critical theories have been proposed in the past to predict the unsteady lift response of an airfoil experiencing vertical gusts by Atassi, and longitudinal gusts by Greenberg. However, their applicability for an airfoil with non-zero angles of attack still needs clarification. Thus, force measurements are conducted to examine these theories’ validity and quasi-steady corrections are applied to compensate potential disparities between the idealised and real flow conditions. Velocity measurements are performed to scrutinise the effect of gusts on the flow around the airfoil, and subsequently to reveal the underlying mechanism governing the airfoil's response to gust-induced perturbations. In the study, two pitching vanes are arranged upstream to generate periodic vertical and longitudinal gusts, whereas a downstream airfoil with angles of attack of 0–12° is subjected to two gust types. It is found that Greenberg's theory demonstrates superior predictive capability in pre-stall regimes, with the potential for its effectiveness to be expanded to post-stall regimes through theoretical refinements. In contrast, Atassi's theory exhibits significant deviations from experimental outcomes across the measured angles of attack. Nevertheless, a modified version of the theory aligns better with experimental results at small angles of attack, whereas substantial discrepancies persist as the angle of attack increases. In the pre-stall regime, the aerodynamic response of the airfoil to vertical gusts displays a linear correlation with the flow angle near the leading edge. In the post-stall regime, the vertical gust induces dynamic stall of the airfoil. The flow angle has an essential effect on the lift coefficient but it alone is inadequate to dictate the trend of the lift coefficient. The vorticity statistics show that negative vortex circulation strongly correlates with the lift coefficient. Thus, further correction of the theory or a new vortex model can be expected to predict the lift variation.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 7
- Cited by



