1. Introduction
A rarefied gas flow past a sphere is a classical problem of fluid mechanics, which is of fundamental importance for understanding the physics of such phenomena as the transport of aerosols in the atmosphere (Davis Reference Davis1997), microfluidics (Kim & Yoo Reference Kim and Yoo2012), security of nuclear plants (Chen et al. Reference Chen, Wang, Mao, Ke, Wen, Tian and Lu2020), dusty gas flows over bodies (Volkov, Tsirkunov & Oesterlé Reference Volkov, Tsirkunov and Oesterlé2005) and two-phase gas–solid particle jets released from solid rocket motors (Carlson & Hoglund Reference Carlson and Hoglund1964; Galkin, Kogan & Fridlender Reference Galkin, Kogan and Fridlender1972; Nelson & Fields Reference Nelson and Fields1996; Aleksandrov & Fridlender Reference Aleksandrov and Fridlender2008). The motion and heat transfer of spherical microparticles and droplets are common for multiple analytical techniques and technological applications, where laser radiation is used for flow characterization or material processing and fabrication, such as laser-induced incandescence (Liu et al. Reference Liu, Daun, Snelling and Smallwood2006), pulsed laser ablation (Volkov & O'Conner Reference Volkov and O'Conner2011; Volkov & Stokes Reference Volkov and Stokes2024) and laser powder-bed fusion additive manufacturing (Stokes et al. Reference Stokes, Khairallah, Volkov and Rubenchik2022). Laser-induced flows with particles are usually characterized by a large temperature difference between particles and surrounding gas as a result of laser heating of particles and, thus, occur under conditions of the strong coupling between particle drag and heat transfer.
Due to the fundamental nature of this problem, the flow past a sphere can be considered as one of the benchmark problems of rarefied gas dynamics (Sharipov Reference Sharipov2012a) and can be used to validate various numerical methods and models. This problem has been investigated in depth in the case of supersonic and hypersonic flows. An analysis of corresponding experimental and computational data with relevant references can be found in the paper by Sharipov & Volkov (Reference Sharipov and Volkov2022). In particular, near-free-molecular, transitional and near-continuum supersonic flows of monatomic gases over a sphere were studied in kinetic simulations based on the direct simulation Monte Carlo (DSMC) method (Bird Reference Bird1994), which represents a stochastic particle-based computational approach for solving problems formulated in terms of the Boltzmann kinetic equation.
The case of subsonic flows over a sphere is characterized by overall smaller degrees of rarefaction and non-equilibrium effects since shock waves in this case do not form. At the same time, as was recognized, for example, by Millikan (Reference Millikan1910) in his oil droplet experiments, the classical Stokes equation (Stokes Reference Stokes1845, Reference Stokes1851) for the sphere drag obtained for incompressible continuum flows fails to predict the drag force on small spheres at small but finite Mach numbers. As is known, when the Reynolds number is smaller than the Mach number, the gas becomes rarefied. However, in most papers on subsonic flows, the Reynolds number is low but still large enough to treat the flowing gas as a continuous medium. The case of transitional subsonic flows over a sphere presents substantial difficulties for both experimental measurements and direct simulations such as DSMC. Indeed, the relative magnitude of statistical noise in DSMC strongly increases with decreasing Mach number, which requires accumulation of extremely large statistical samples to obtain statistically meaningful results. As a result, the experimental and computational literature data on sphere drag and heat transfer in transitional subsonic flows are very poor. Bailey (Reference Bailey1974) reported experimental drag coefficients for the ranges of ![]() $Ma<0.2$ and
$Ma<0.2$ and ![]() $Re\ge 0.01$. At larger Reynolds numbers, experimental data for the sphere drag were obtained by Bailey & Hiatt (Reference Bailey and Hiatt1971) and Roos & Willmarth (Reference Roos and Willmarth1971). A three-dimensional flow past a rotating sphere at
$Re\ge 0.01$. At larger Reynolds numbers, experimental data for the sphere drag were obtained by Bailey & Hiatt (Reference Bailey and Hiatt1971) and Roos & Willmarth (Reference Roos and Willmarth1971). A three-dimensional flow past a rotating sphere at ![]() $Ma=0.2$ was considered in DSMC simulations by Volkov (Reference Volkov2009, Reference Volkov2011). Other experimental and computational results for a subsonic sphere drag were summarized by Loth et al. (Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021), who also developed an accurate semi-empirical equation for the sphere drag coefficient. Another semi-empirical equation for the sphere drag coefficient accounting for the rarefaction and compressibility effects was developed by Henderson (Reference Henderson1976). The latter also accounts for the difference between the sphere and free-stream temperatures. The heat transfer of a sphere at rest in the transitional regime was considered in DSMC simulations by Filippov & Rosner (Reference Filippov and Rosner2000) and Liu et al. (Reference Liu, Daun, Snelling and Smallwood2006). The experimental results for the sphere heat transfer in subsonic transitional flows were summarized by Kavanau (Reference Kavanau1955) and Koshmarov & Svirshevskii (Reference Koshmarov and Svirshevskii1993), who also developed semi-empirical equations for the sphere Nusselt number and adiabatic temperature. However, the accuracy of such coarse approximations is questionable.
$Ma=0.2$ was considered in DSMC simulations by Volkov (Reference Volkov2009, Reference Volkov2011). Other experimental and computational results for a subsonic sphere drag were summarized by Loth et al. (Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021), who also developed an accurate semi-empirical equation for the sphere drag coefficient. Another semi-empirical equation for the sphere drag coefficient accounting for the rarefaction and compressibility effects was developed by Henderson (Reference Henderson1976). The latter also accounts for the difference between the sphere and free-stream temperatures. The heat transfer of a sphere at rest in the transitional regime was considered in DSMC simulations by Filippov & Rosner (Reference Filippov and Rosner2000) and Liu et al. (Reference Liu, Daun, Snelling and Smallwood2006). The experimental results for the sphere heat transfer in subsonic transitional flows were summarized by Kavanau (Reference Kavanau1955) and Koshmarov & Svirshevskii (Reference Koshmarov and Svirshevskii1993), who also developed semi-empirical equations for the sphere Nusselt number and adiabatic temperature. However, the accuracy of such coarse approximations is questionable.
In the case of extremely small Mach numbers, the kinetic equations can be linearized, opening a way for asymptotic solution of rarefied gas dynamics problems (Sharipov Reference Sharipov2016). As a result, the flow of a rarefied gas past a sphere in the limit of small Mach number was intensively studied (e.g. Cercignani, Pagani & Bassanini Reference Cercignani, Pagani and Bassanini1968; Beresnev, Chernyak & Fomyagin Reference Beresnev, Chernyak and Fomyagin1990; Loyalka Reference Loyalka1992; Lima Bernardo, Moraes & Rosas Reference Lima Bernardo, Moraes and Rosas2013; Kalempa & Sharipov Reference Kalempa and Sharipov2020, Reference Kalempa and Sharipov2022; Taguchi & Tsuji Reference Taguchi and Tsuji2022). A similar linearization technique was also used to predict the temperature field around a sphere and local heat transfer when the temperatures of the surface and stream are the same (e.g. Aoki & Sone Reference Aoki and Sone1987). Under such conditions, the drag coefficient is proportional to the Mach number, while the average energy transfer coefficient just vanishes. It is quite clear that such solutions cannot be directly extended to the case of finite Mach numbers, and the exact range of applicability of these solutions can be established only by comparing the results of the linear theory with those based on the full kinetic equation.
The aim of the present paper is to calculate aerothermodynamic characteristics of a sphere in the subsonic flow regime over a wide range of gas rarefaction. To this end, systematic simulations of flows using the DSMC method based on ab initio potentials (Sharipov & Strapasson Reference Sharipov and Strapasson2012) are performed for various noble gases in the range of Mach number from ![]() $0.1$ to 1. In the simulations, the rarefaction parameter varies in the range from
$0.1$ to 1. In the simulations, the rarefaction parameter varies in the range from ![]() $0$ to
$0$ to ![]() $10$, which spans the free-molecular, transitional and slip-flow regimes. The simulations are targeted at four specific goals, which have not been addressed in the literature. First, we point out the effect of gas species on both drag and heat transfer coefficients. Second, we compare the sphere drag coefficients with the predictions of the linear theory to find the range of applicability of this theory. Third, we study the effects of the incomplete gas–surface accommodation using the scattering model proposed by Cercignani & Lampis (Reference Cercignani and Lampis1971) for several sets of tangential momentum accommodation coefficient (TMAC) and normal energy accommodation coefficient (NEAC). Fourth, we consider a broad range of gas–surface temperature ratios to reveal the effects of coupling between sphere drag and heat transfer in subsonic flows.
$10$, which spans the free-molecular, transitional and slip-flow regimes. The simulations are targeted at four specific goals, which have not been addressed in the literature. First, we point out the effect of gas species on both drag and heat transfer coefficients. Second, we compare the sphere drag coefficients with the predictions of the linear theory to find the range of applicability of this theory. Third, we study the effects of the incomplete gas–surface accommodation using the scattering model proposed by Cercignani & Lampis (Reference Cercignani and Lampis1971) for several sets of tangential momentum accommodation coefficient (TMAC) and normal energy accommodation coefficient (NEAC). Fourth, we consider a broad range of gas–surface temperature ratios to reveal the effects of coupling between sphere drag and heat transfer in subsonic flows.
2. Statement of the problem
In the present work, the problem is formulated in the form that was previously used by Sharipov & Volkov (Reference Sharipov and Volkov2022) for supersonic flows over a sphere. A sphere of radius ![]() $R$ at rest is streamlined by a dilute gas. Far from the sphere, the equilibrium monatomic gas at pressure
$R$ at rest is streamlined by a dilute gas. Far from the sphere, the equilibrium monatomic gas at pressure ![]() $p_\infty$ and temperature
$p_\infty$ and temperature ![]() $T_\infty$ flows with a constant bulk velocity
$T_\infty$ flows with a constant bulk velocity ![]() $U_\infty$ as shown in figure 1. The temperature of the sphere surface
$U_\infty$ as shown in figure 1. The temperature of the sphere surface ![]() $T_w$ can be different from the free-stream temperature
$T_w$ can be different from the free-stream temperature ![]() $T_\infty$. The primary goal of the simulations is to find the local stress and energy coefficients at the sphere surface, as well as the drag and average energy transfer coefficients for the whole sphere.
$T_\infty$. The primary goal of the simulations is to find the local stress and energy coefficients at the sphere surface, as well as the drag and average energy transfer coefficients for the whole sphere.

Figure 1. Scheme of the flow.
The main factors that determine the solution of the problem are the Mach number ![]() $Ma$ and rarefaction parameter
$Ma$ and rarefaction parameter ![]() $\delta$ (Sharipov Reference Sharipov2016) defined as
$\delta$ (Sharipov Reference Sharipov2016) defined as
respectively. Here ![]() $c_s=\sqrt {\gamma k_{{B}} T_\infty /m}$ is the sound speed,
$c_s=\sqrt {\gamma k_{{B}} T_\infty /m}$ is the sound speed, ![]() $\gamma =c_p/c_v=5/3$ is the specific heat ratio,
$\gamma =c_p/c_v=5/3$ is the specific heat ratio, ![]() $\mu _\infty$ is the gas viscosity at temperature
$\mu _\infty$ is the gas viscosity at temperature ![]() $T_\infty$,
$T_\infty$, ![]() $v_\infty =\sqrt {{2k_{{B}} T_\infty }/{m}}$ is the most probable speed of gas atoms at temperature
$v_\infty =\sqrt {{2k_{{B}} T_\infty }/{m}}$ is the most probable speed of gas atoms at temperature ![]() $T_\infty$,
$T_\infty$, ![]() $k_{{B}}$ is the Boltzmann constant and
$k_{{B}}$ is the Boltzmann constant and ![]() $m$ is the mass of a gas atom. The Reynolds number is related to
$m$ is the mass of a gas atom. The Reynolds number is related to ![]() $Ma$ and
$Ma$ and ![]() $\delta$ as
$\delta$ as
where ![]() $\rho _\infty =mp_\infty /(k_{{B}} T_\infty )$ is the gas density in the free stream.
$\rho _\infty =mp_\infty /(k_{{B}} T_\infty )$ is the gas density in the free stream.
The quantities of our interest are the pressure ![]() $C_p$, friction
$C_p$, friction ![]() $C_f$ and energy transfer
$C_f$ and energy transfer ![]() $C_h$ coefficients defined as
$C_h$ coefficients defined as
where ![]() $p_n$ is the stress normal to the sphere surface,
$p_n$ is the stress normal to the sphere surface, ![]() $\tau$ is the shear stress on the surface and
$\tau$ is the shear stress on the surface and ![]() $J_e$ is the energy flux from the surface. The drag
$J_e$ is the energy flux from the surface. The drag ![]() $C_D$ and average energy transfer
$C_D$ and average energy transfer ![]() $C_Q$ coefficients are defined as
$C_Q$ coefficients are defined as
where ![]() $F$ is the drag force exerted on the sphere and
$F$ is the drag force exerted on the sphere and ![]() $Q$ is the total energy flux from the gas to the sphere surface.
$Q$ is the total energy flux from the gas to the sphere surface.
The coefficients ![]() $C_D$ and
$C_D$ and ![]() $C_Q$ are widely used to determine the drag force and energy flux of a sphere in supersonic and hypersonic flows. In subsonic flows at
$C_Q$ are widely used to determine the drag force and energy flux of a sphere in supersonic and hypersonic flows. In subsonic flows at ![]() $T_w=T_\infty$, these coefficients diverge as
$T_w=T_\infty$, these coefficients diverge as ![]() $1/Ma$ when
$1/Ma$ when ![]() $Ma\to 0$. To avoid this singularity, the computation results in this work are also presented in the form of the reduced coefficients
$Ma\to 0$. To avoid this singularity, the computation results in this work are also presented in the form of the reduced coefficients
In addition, at ![]() $T_w\ne T_\infty$, the coefficients
$T_w\ne T_\infty$, the coefficients ![]() $C_h$ and
$C_h$ and ![]() $C_Q$ vary inversely proportional to
$C_Q$ vary inversely proportional to ![]() $Ma^3$ when
$Ma^3$ when ![]() $Ma\to 0$, so that the energy transfer of the sphere is also characterized by the coefficients
$Ma\to 0$, so that the energy transfer of the sphere is also characterized by the coefficients
The solution of the problem is uniquely defined by the Mach number ![]() $Ma$, rarefaction parameter
$Ma$, rarefaction parameter ![]() $\delta$, temperature ratio
$\delta$, temperature ratio ![]() $T_w/T_\infty$ and other similarity parameters that depend on the parameters of the adopted model of binary collisions between gas atoms and model of gas–surface interaction (Volkov & Sharipov Reference Volkov and Sharipov2017). The binary collisions between atoms of noble gases are described by the solution of the quantum mechanical scattering problem (Joachain Reference Joachain1975) and interatomic interaction potentials established in ab initio quantum mechanical calculations as suggested by Aziz, Janzen & Moldover (Reference Aziz, Janzen and Moldover1995). The simulations are performed for helium (
$T_w/T_\infty$ and other similarity parameters that depend on the parameters of the adopted model of binary collisions between gas atoms and model of gas–surface interaction (Volkov & Sharipov Reference Volkov and Sharipov2017). The binary collisions between atoms of noble gases are described by the solution of the quantum mechanical scattering problem (Joachain Reference Joachain1975) and interatomic interaction potentials established in ab initio quantum mechanical calculations as suggested by Aziz, Janzen & Moldover (Reference Aziz, Janzen and Moldover1995). The simulations are performed for helium (![]() $^4$He), neon and krypton using the interatomic potentials obtained by Cencek et al. (Reference Cencek, Przybytek, Komasa, Mehl, Jeziorski and Szalewicz2012), Hellmann, Bich & Vogel (Reference Hellmann, Bich and Vogel2008) and Jäger et al. (Reference Jäger, Hellmann, Bich and Vogel2016), respectively. For helium, additional test simulations at
$^4$He), neon and krypton using the interatomic potentials obtained by Cencek et al. (Reference Cencek, Przybytek, Komasa, Mehl, Jeziorski and Szalewicz2012), Hellmann, Bich & Vogel (Reference Hellmann, Bich and Vogel2008) and Jäger et al. (Reference Jäger, Hellmann, Bich and Vogel2016), respectively. For helium, additional test simulations at ![]() $Ma=0.2$ and various
$Ma=0.2$ and various ![]() $\delta$ were also performed using the ab initio potential recently found in quantum Monte Carlo simulation by Kayang et al. (Reference Kayang, Volkov, Zhilyaev and Sharipov2023). The simulations based on the potentials by Kayang et al. (Reference Kayang, Volkov, Zhilyaev and Sharipov2023) and Cencek et al. (Reference Cencek, Przybytek, Komasa, Mehl, Jeziorski and Szalewicz2012) resulted in values of
$\delta$ were also performed using the ab initio potential recently found in quantum Monte Carlo simulation by Kayang et al. (Reference Kayang, Volkov, Zhilyaev and Sharipov2023). The simulations based on the potentials by Kayang et al. (Reference Kayang, Volkov, Zhilyaev and Sharipov2023) and Cencek et al. (Reference Cencek, Przybytek, Komasa, Mehl, Jeziorski and Szalewicz2012) resulted in values of ![]() $C_D$ and
$C_D$ and ![]() $C_Q$ that are different by less than 1.5 %. To describe the gas–surface interaction, the model proposed by Cercignani & Lampis (Reference Cercignani and Lampis1971) is employed. It includes TMAC and NEAC hereinafter denoted as
$C_Q$ that are different by less than 1.5 %. To describe the gas–surface interaction, the model proposed by Cercignani & Lampis (Reference Cercignani and Lampis1971) is employed. It includes TMAC and NEAC hereinafter denoted as ![]() $\alpha _t$ and
$\alpha _t$ and ![]() $\alpha _n$, respectively. The main results reported here are obtained assuming the full accommodation on the sphere surface, i.e. diffuse scattering with
$\alpha _n$, respectively. The main results reported here are obtained assuming the full accommodation on the sphere surface, i.e. diffuse scattering with ![]() $\alpha _t=1$ and
$\alpha _t=1$ and ![]() $\alpha _n=1$. Like in the paper by Sharipov & Volkov (Reference Sharipov and Volkov2022), the calculations are also performed for helium using two sets of TMAC and NEAC: (i)
$\alpha _n=1$. Like in the paper by Sharipov & Volkov (Reference Sharipov and Volkov2022), the calculations are also performed for helium using two sets of TMAC and NEAC: (i) ![]() $\alpha _t = 0.4$ and
$\alpha _t = 0.4$ and ![]() $\alpha _n = 0.01$; (ii)
$\alpha _n = 0.01$; (ii) ![]() $\alpha _t = 0.9$ and
$\alpha _t = 0.9$ and ![]() $\alpha _n = 0.1$. The former corresponds to a treated and polished metal surface, while the latter describes the interaction of helium with a non-treated surface (Sharipov & Moldover Reference Sharipov and Moldover2016). A third set of accommodation coefficients for neon, (iii)
$\alpha _n = 0.1$. The former corresponds to a treated and polished metal surface, while the latter describes the interaction of helium with a non-treated surface (Sharipov & Moldover Reference Sharipov and Moldover2016). A third set of accommodation coefficients for neon, (iii) ![]() $\alpha _t = 0.9$ and
$\alpha _t = 0.9$ and ![]() $\alpha _n = 0.85$, is used to characterize the effect of the deviations from diffuse scattering, which is observed experimentally for technical surfaces without special treatment (Sharipov & Bertoldo Reference Sharipov and Bertoldo2006).
$\alpha _n = 0.85$, is used to characterize the effect of the deviations from diffuse scattering, which is observed experimentally for technical surfaces without special treatment (Sharipov & Bertoldo Reference Sharipov and Bertoldo2006).
The DSMC simulations are performed at ![]() $Ma=0.1$,
$Ma=0.1$, ![]() $0.2$,
$0.2$, ![]() $0.5$ and
$0.5$ and ![]() $1$ for
$1$ for ![]() $\delta =0.1$,
$\delta =0.1$, ![]() $0.3$,
$0.3$, ![]() $1$,
$1$, ![]() $3$ and
$3$ and ![]() $10$ with
$10$ with ![]() $T_\infty =300$ K and sphere temperature
$T_\infty =300$ K and sphere temperature ![]() $T_w$ equal to
$T_w$ equal to ![]() $100$,
$100$, ![]() $150$,
$150$, ![]() $300$,
$300$, ![]() $600$ and
$600$ and ![]() $1000$ K. The values of the drag and average energy transfer coefficients at
$1000$ K. The values of the drag and average energy transfer coefficients at ![]() $Ma=1$ for various
$Ma=1$ for various ![]() $\delta$,
$\delta$, ![]() $T_\infty =T_w=300$ K and diffuse scattering obtained previously by Sharipov & Volkov (Reference Sharipov and Volkov2022) are used in the present work without changes.
$T_\infty =T_w=300$ K and diffuse scattering obtained previously by Sharipov & Volkov (Reference Sharipov and Volkov2022) are used in the present work without changes.
3. Free-molecular and continuum flow limits
The expressions for ![]() $C_D$ and
$C_D$ and ![]() $C_Q$ for a sphere in the free-molecular flow regime with the Cercignani–Lampis surface scattering kernel at arbitrary
$C_Q$ for a sphere in the free-molecular flow regime with the Cercignani–Lampis surface scattering kernel at arbitrary ![]() $Ma$,
$Ma$, ![]() $\alpha _t$ and
$\alpha _t$ and ![]() $\alpha _n$ were obtained by Sharipov & Volkov (Reference Sharipov and Volkov2022) in the form
$\alpha _n$ were obtained by Sharipov & Volkov (Reference Sharipov and Volkov2022) in the form
 \begin{gather} \begin{aligned}\varPhi(\alpha_n,\xi) &= \frac{2}{{\rm \pi}^{3/2} S^2 \alpha_n (T_w/T_\infty)} \int_0^\infty \int_0^\infty \int_0^{2{\rm \pi}} c^2 c' \nonumber\\ &\quad \times\exp\left(-\frac{c^2+(1-\alpha_n)c^{\prime 2}- 2\sqrt{1-\alpha_n}cc'\cos\phi}{\alpha_n (T_w/T_\infty)}-(c'-\xi)^2\right)\,\mbox{d} \phi \,\mbox{d} c' \,\mbox{d} c,\end{aligned} \end{gather}
\begin{gather} \begin{aligned}\varPhi(\alpha_n,\xi) &= \frac{2}{{\rm \pi}^{3/2} S^2 \alpha_n (T_w/T_\infty)} \int_0^\infty \int_0^\infty \int_0^{2{\rm \pi}} c^2 c' \nonumber\\ &\quad \times\exp\left(-\frac{c^2+(1-\alpha_n)c^{\prime 2}- 2\sqrt{1-\alpha_n}cc'\cos\phi}{\alpha_n (T_w/T_\infty)}-(c'-\xi)^2\right)\,\mbox{d} \phi \,\mbox{d} c' \,\mbox{d} c,\end{aligned} \end{gather}
where ![]() $S=U_\infty /v_\infty$,
$S=U_\infty /v_\infty$, ![]() $\xi =S\cos \theta$ and
$\xi =S\cos \theta$ and ![]() $\mbox {erf}(S)$ is the error function. These expressions are consistent with those obtained for a flat plate by Cercignani & Lampis (Reference Cercignani and Lampis1972).
$\mbox {erf}(S)$ is the error function. These expressions are consistent with those obtained for a flat plate by Cercignani & Lampis (Reference Cercignani and Lampis1972).
The calculations of the drag ![]() $C_D^*$ and average heat transfer
$C_D^*$ and average heat transfer ![]() $C_Q^*$ coefficients with (3.1) and (3.2) as functions of TMAC
$C_Q^*$ coefficients with (3.1) and (3.2) as functions of TMAC ![]() $\alpha _t$ and NEAC
$\alpha _t$ and NEAC ![]() $\alpha _n$ at
$\alpha _n$ at ![]() $Ma=0.2$ indicate that the variation of
$Ma=0.2$ indicate that the variation of ![]() $\alpha _n$ has qualitatively different effects on
$\alpha _n$ has qualitatively different effects on ![]() $C_D^*$ and
$C_D^*$ and ![]() $C_Q^*$ at
$C_Q^*$ at ![]() $T_w/T_\infty = 1$ and
$T_w/T_\infty = 1$ and ![]() $T_w/T_\infty > 1$ (see supplementary material available at https://doi.org/10.1017/jfm.2024.1036). In a nearly isothermal flow at
$T_w/T_\infty > 1$ (see supplementary material available at https://doi.org/10.1017/jfm.2024.1036). In a nearly isothermal flow at ![]() $T_w/T_\infty = 1$,
$T_w/T_\infty = 1$, ![]() $C_D^*$ decreases and
$C_D^*$ decreases and ![]() $C_Q^*$ increases with increasing
$C_Q^*$ increases with increasing ![]() $\alpha _n$. However, these trends are reversed at
$\alpha _n$. However, these trends are reversed at ![]() $T_w/T_\infty > 1$.
$T_w/T_\infty > 1$.
For the purposes of the present work, it is instructive to obtain the series expansions of ![]() $C_D^*$,
$C_D^*$, ![]() $C_Q^*$ and
$C_Q^*$ and ![]() $C_Q^{**}$ considering the Mach number
$C_Q^{**}$ considering the Mach number ![]() $Ma$ as a small parameter. The series expansion of the function
$Ma$ as a small parameter. The series expansion of the function ![]() $\varPhi (\alpha _n,\xi )$ given by (3.3) with respect to
$\varPhi (\alpha _n,\xi )$ given by (3.3) with respect to ![]() $\xi$ takes the form
$\xi$ takes the form
 \begin{align} \varPhi(\alpha_n,\xi) &= \varPhi_1(\alpha_n)+2\varPhi_2(\alpha_n)\xi +[2\varPhi_3(\alpha_n)-\varPhi_1(\alpha_n)]\xi^2 \nonumber\\ &\quad +\tfrac23[2\varPhi_4(\alpha_n)-3\varPhi_2(\alpha_n)]\xi^3+O(\xi^4), \end{align}
\begin{align} \varPhi(\alpha_n,\xi) &= \varPhi_1(\alpha_n)+2\varPhi_2(\alpha_n)\xi +[2\varPhi_3(\alpha_n)-\varPhi_1(\alpha_n)]\xi^2 \nonumber\\ &\quad +\tfrac23[2\varPhi_4(\alpha_n)-3\varPhi_2(\alpha_n)]\xi^3+O(\xi^4), \end{align}where
 \begin{align} \varPhi_m(\alpha_n) &= \frac{2}{{\rm \pi}\alpha_n (T_w/T_\infty)}\int_0^\infty \int_0^\infty \int_0^{2{\rm \pi}} c^2 c^{\prime m} \nonumber\\ &\quad \times \exp\left(-\frac{c^2+(1-\alpha_n)c^{\prime 2}- 2\sqrt{1-\alpha_n}cc'\cos\phi}{\alpha_n (T_w/T_\infty)}-c'^2\right)\mbox{d} \phi \,\mbox{d} c' \,\mbox{d} c. \end{align}
\begin{align} \varPhi_m(\alpha_n) &= \frac{2}{{\rm \pi}\alpha_n (T_w/T_\infty)}\int_0^\infty \int_0^\infty \int_0^{2{\rm \pi}} c^2 c^{\prime m} \nonumber\\ &\quad \times \exp\left(-\frac{c^2+(1-\alpha_n)c^{\prime 2}- 2\sqrt{1-\alpha_n}cc'\cos\phi}{\alpha_n (T_w/T_\infty)}-c'^2\right)\mbox{d} \phi \,\mbox{d} c' \,\mbox{d} c. \end{align}
When (3.6) is inserted into (3.1), the terms containing ![]() $\varPhi _1$ and
$\varPhi _1$ and ![]() $\varPhi _3$ disappear and only
$\varPhi _3$ disappear and only ![]() $\varPhi _2$ and
$\varPhi _2$ and ![]() $\varPhi _4$ need to be calculated. In the limit of
$\varPhi _4$ need to be calculated. In the limit of ![]() $\alpha _n\to 0$, the functions
$\alpha _n\to 0$, the functions ![]() $\varPhi _2$ and
$\varPhi _2$ and ![]() $\varPhi _4$ become
$\varPhi _4$ become
The extremely small values of ![]() $\alpha _n\sim 0.01$ were extracted by Sharipov & Moldover (Reference Sharipov and Moldover2016) from the experimental data on the heat flux between helium and machined steel surface reported by Trott et al. (Reference Trott, Castaneda, Torczynski, Gallis and Rader2011). Therefore, the limit of
$\alpha _n\sim 0.01$ were extracted by Sharipov & Moldover (Reference Sharipov and Moldover2016) from the experimental data on the heat flux between helium and machined steel surface reported by Trott et al. (Reference Trott, Castaneda, Torczynski, Gallis and Rader2011). Therefore, the limit of ![]() $\alpha _n\to 0$ can practically occur. In the opposite limit of
$\alpha _n\to 0$ can practically occur. In the opposite limit of ![]() $\alpha _n\to 1$, (3.7) reduces to
$\alpha _n\to 1$, (3.7) reduces to
 \begin{equation} \varPhi_2=\frac{\rm \pi}{4}\left(\frac{T_w}{T_\infty}\right)^{1/2},\quad \varPhi_4=\frac{3{\rm \pi}}{8}\left(\frac{T_w}{T_\infty}\right)^{1/2}.\end{equation}
\begin{equation} \varPhi_2=\frac{\rm \pi}{4}\left(\frac{T_w}{T_\infty}\right)^{1/2},\quad \varPhi_4=\frac{3{\rm \pi}}{8}\left(\frac{T_w}{T_\infty}\right)^{1/2}.\end{equation}This limit is typical for heavy gases like krypton.
An expansion of ![]() $\varPsi _1(S)$ and
$\varPsi _1(S)$ and ![]() $\varPsi _2(S)$ given by (3.4) and (3.5) with respect to
$\varPsi _2(S)$ given by (3.4) and (3.5) with respect to ![]() $S$ in combination with (3.6) leads to the following expression for the reduced drag coefficient:
$S$ in combination with (3.6) leads to the following expression for the reduced drag coefficient:
Thus, the drag coefficient ![]() $C_D^*$ quickly converges to its limit value
$C_D^*$ quickly converges to its limit value ![]() $8\sqrt {2/(15{\rm \pi} )}(1+\alpha _t+\varPhi _2)$ at
$8\sqrt {2/(15{\rm \pi} )}(1+\alpha _t+\varPhi _2)$ at ![]() $Ma\to 0$ and arbitrary
$Ma\to 0$ and arbitrary ![]() $T_w/T_\infty$. Even at a relatively large Mach number, the contribution of the term of the order of
$T_w/T_\infty$. Even at a relatively large Mach number, the contribution of the term of the order of ![]() $Ma^2$ remains small and, for example, does not exceed 1 % at
$Ma^2$ remains small and, for example, does not exceed 1 % at ![]() ${Ma} \le 0.3$. The limit value of
${Ma} \le 0.3$. The limit value of ![]() $C_D^*$ at
$C_D^*$ at ![]() ${Ma} \to 0$ agrees with those obtained by Kalempa & Sharipov (Reference Kalempa and Sharipov2020).
${Ma} \to 0$ agrees with those obtained by Kalempa & Sharipov (Reference Kalempa and Sharipov2020).
The series expansions of the energy transfer coefficient ![]() $C_Q$ in terms of
$C_Q$ in terms of ![]() $Ma$ have different forms in the cases when
$Ma$ have different forms in the cases when ![]() $T_w=T_\infty$ and
$T_w=T_\infty$ and ![]() $T_w\ne T_\infty$. At
$T_w\ne T_\infty$. At ![]() $T_w=T_\infty$, the expansion of the coefficient
$T_w=T_\infty$, the expansion of the coefficient ![]() $C_Q^*$ takes the form
$C_Q^*$ takes the form
This coefficient also quickly converges to its limit value at ![]() $Ma\to 0$. At
$Ma\to 0$. At ![]() $T_w\ne T_\infty$, the expansion of the coefficient
$T_w\ne T_\infty$, the expansion of the coefficient ![]() $C_Q^{**}$ results in
$C_Q^{**}$ results in
The differences between (3.11) and (3.12) reflect the fact that, when ![]() $T_w\neq T_\infty$ and
$T_w\neq T_\infty$ and ![]() $Ma\ll 1$, the heat flux is dominated by the temperature difference between the sphere and surrounding gas and only weakly affected by the sphere motion.
$Ma\ll 1$, the heat flux is dominated by the temperature difference between the sphere and surrounding gas and only weakly affected by the sphere motion.
The numerical values of the drag coefficient ![]() $C_D^*$ in the free-molecular flow regime calculated for
$C_D^*$ in the free-molecular flow regime calculated for ![]() $T_w=T_\infty$ and several combinations of
$T_w=T_\infty$ and several combinations of ![]() $\alpha _t$ and
$\alpha _t$ and ![]() $\alpha _n$ from the expressions obtained by Sharipov & Volkov (Reference Sharipov and Volkov2022) are compared with the limit values corresponding to
$\alpha _n$ from the expressions obtained by Sharipov & Volkov (Reference Sharipov and Volkov2022) are compared with the limit values corresponding to ![]() $Ma\to 0$ in table 1. It can be seen that the values of
$Ma\to 0$ in table 1. It can be seen that the values of ![]() $C_D^*$ at
$C_D^*$ at ![]() $Ma=0.2$ are close to those in the limit of
$Ma=0.2$ are close to those in the limit of ![]() $Ma\to 0$ with the difference being smaller than 1 %. These results also demonstrate that the variation of the TMAC and NEAC in the gas–surface interaction model can change
$Ma\to 0$ with the difference being smaller than 1 %. These results also demonstrate that the variation of the TMAC and NEAC in the gas–surface interaction model can change ![]() $C_D^*$ by 23 %. The largest values of
$C_D^*$ by 23 %. The largest values of ![]() $C_D^*$ correspond to the combination
$C_D^*$ correspond to the combination ![]() $\alpha _t=0.9$ and
$\alpha _t=0.9$ and ![]() $\alpha _n=0.1$, while the smallest values of
$\alpha _n=0.1$, while the smallest values of ![]() $C_D^*$ are obtained at
$C_D^*$ are obtained at ![]() $\alpha _t=0.4$ and
$\alpha _t=0.4$ and ![]() $\alpha _n=0.3$.
$\alpha _n=0.3$.
Table 1. Drag coefficient ![]() $C_D^*$ versus accommodation coefficients
$C_D^*$ versus accommodation coefficients ![]() $\alpha _t$,
$\alpha _t$, ![]() $\alpha _n$ and Mach number
$\alpha _n$ and Mach number ![]() $Ma$ in the free-molecular regime (
$Ma$ in the free-molecular regime (![]() $\delta \to 0$) at
$\delta \to 0$) at ![]() $T_w=T_\infty$.
$T_w=T_\infty$.

In the continuum regime (![]() $\delta \to \infty$) and at small Mach number (
$\delta \to \infty$) and at small Mach number (![]() $Ma\to 0$), the drag coefficient is defined by the Stokes (Reference Stokes1851) equation, which is the linearized Navier–Stokes equation. Alternatively, the Stokes equation can be derived from the linearized Boltzmann equation. Taking into account the Oseen (Reference Oseen1910, Reference Oseen1913) correction, the drag coefficient is obtained in terms of
$Ma\to 0$), the drag coefficient is defined by the Stokes (Reference Stokes1851) equation, which is the linearized Navier–Stokes equation. Alternatively, the Stokes equation can be derived from the linearized Boltzmann equation. Taking into account the Oseen (Reference Oseen1910, Reference Oseen1913) correction, the drag coefficient is obtained in terms of ![]() $Ma$ and
$Ma$ and ![]() $\delta$ as
$\delta$ as
 \begin{equation} C_D^*=\frac{6\sqrt{30}}{5\delta}\left(1+\frac{\sqrt{30}}{8} \delta Ma\right), \end{equation}
\begin{equation} C_D^*=\frac{6\sqrt{30}}{5\delta}\left(1+\frac{\sqrt{30}}{8} \delta Ma\right), \end{equation}
where (2.2) was used. This expression indicates that the nonlinear correction has the order of ![]() ${\delta}Ma$ and it increases when the rarefaction parameter
${\delta}Ma$ and it increases when the rarefaction parameter ![]() $\delta$ increases.
$\delta$ increases.
Thus, the convergence of ![]() $C_D^*$ to the linear solution is slow at large values of
$C_D^*$ to the linear solution is slow at large values of ![]() $\delta$ according to (3.13), while the convergence is fast at small
$\delta$ according to (3.13), while the convergence is fast at small ![]() $\delta$ in agreement with (3.10). The results reported below show the convergence at intermediate values of
$\delta$ in agreement with (3.10). The results reported below show the convergence at intermediate values of ![]() $\delta$. More detailed analysis of the contribution of the nonlinear terms to the drag coefficient is given by Taguchi & Tsuji (Reference Taguchi and Tsuji2022), where the series expansion of the Boltzmann equation proposed by Sharipov (Reference Sharipov2012b) was used. To reduce the magnitude of the nonlinear correction below 1 % at
$\delta$. More detailed analysis of the contribution of the nonlinear terms to the drag coefficient is given by Taguchi & Tsuji (Reference Taguchi and Tsuji2022), where the series expansion of the Boltzmann equation proposed by Sharipov (Reference Sharipov2012b) was used. To reduce the magnitude of the nonlinear correction below 1 % at ![]() $\delta =10$, the Mach number should be smaller than
$\delta =10$, the Mach number should be smaller than ![]() $10^{-3}$. Such small values of
$10^{-3}$. Such small values of ![]() $Ma$ are inaccessible by the DSMC method. Therefore, a solution of the full kinetic equation by the discrete velocity method is necessary in order to find the applicability range of the linear theory in the near-continuum regime.
$Ma$ are inaccessible by the DSMC method. Therefore, a solution of the full kinetic equation by the discrete velocity method is necessary in order to find the applicability range of the linear theory in the near-continuum regime.
4. Numerical method for the transitional flow regime
Two-dimensional axisymmetric simulations of rarefied gas flows over a sphere in the transitional flow regime are performed using the DSMC method previously applied for supersonic flows over a sphere by Sharipov & Volkov (Reference Sharipov and Volkov2022). The sampling of intermolecular collisions in this method is based on the ab initio interatomic potentials. The intermolecular collision procedure was previously validated in calculations of viscosity and thermal conductivity by the DSMC method over a wide temperature range (Sharipov Reference Sharipov2022).
The high-fidelity DSMC calculations of subsonic flows are challenging and require careful choice of numerical parameters. In simulations, the computational domain represents a cylinder of radius ![]() $R_d$ and length
$R_d$ and length ![]() $2R_d$ with the sphere placed in its centre. The domain is divided into a regular mesh of cells, where each cell has a shape of a torus of size
$2R_d$ with the sphere placed in its centre. The domain is divided into a regular mesh of cells, where each cell has a shape of a torus of size ![]() $\Delta x$ in the radial and axial directions. The time is discretized and advanced by the time step
$\Delta x$ in the radial and axial directions. The time is discretized and advanced by the time step ![]() $\Delta t$. The numerical error is determined by the size of the computational domain
$\Delta t$. The numerical error is determined by the size of the computational domain ![]() $R_d$, cell size
$R_d$, cell size ![]() $\Delta x$, number of modelling particles per cell
$\Delta x$, number of modelling particles per cell ![]() $N_p$ in the free stream, time step
$N_p$ in the free stream, time step ![]() $\Delta t$, number of time steps
$\Delta t$, number of time steps ![]() $N_{{steady}}$ required to establish steady-state flow and number of time steps
$N_{{steady}}$ required to establish steady-state flow and number of time steps ![]() $N_s$ used to sample parameters of simulated particles for further calculation of macroscopic gas quantities. The optimum values of these parameters were chosen in a series of preliminary simulations. An analysis of the numerical errors and convergence of
$N_s$ used to sample parameters of simulated particles for further calculation of macroscopic gas quantities. The optimum values of these parameters were chosen in a series of preliminary simulations. An analysis of the numerical errors and convergence of ![]() $C_D^*$ and
$C_D^*$ and ![]() $C_Q^*$ at variation of numerical scheme parameters are presented in the supplementary material, which shows that the numerical error in the drag coefficient
$C_Q^*$ at variation of numerical scheme parameters are presented in the supplementary material, which shows that the numerical error in the drag coefficient ![]() $C_D^*$ does not exceed 0.5 % under all conditions considered here and the numerical error in the average energy transfer coefficient
$C_D^*$ does not exceed 0.5 % under all conditions considered here and the numerical error in the average energy transfer coefficient ![]() $C_Q^*$ does not exceed 1 % at
$C_Q^*$ does not exceed 1 % at ![]() ${Ma} \ge 0.2$. It has been found that at
${Ma} \ge 0.2$. It has been found that at ![]() $Ma=0.1$ the fluctuation of
$Ma=0.1$ the fluctuation of ![]() $C_Q^*$ in time remains relatively high even after an excessively large number of sampling time steps
$C_Q^*$ in time remains relatively high even after an excessively large number of sampling time steps ![]() $N_s$. In this case, the maximum numerical error of
$N_s$. In this case, the maximum numerical error of ![]() $C_Q^*$ is estimated to be at a level of1 %–4 %.
$C_Q^*$ is estimated to be at a level of1 %–4 %.
The optimum value of each numerical scheme parameter depends on both Mach number ![]() $Ma$ and rarefaction parameter
$Ma$ and rarefaction parameter ![]() $\delta$. The relative size of the computational domain
$\delta$. The relative size of the computational domain ![]() $R_d/R$ and the cell size
$R_d/R$ and the cell size ![]() $\Delta x/R$ for all considered
$\Delta x/R$ for all considered ![]() $Ma$ and
$Ma$ and ![]() $\delta$ are given in table 2. The time step varies from
$\delta$ are given in table 2. The time step varies from ![]() $\Delta t=0.002 R/v_\infty$ at
$\Delta t=0.002 R/v_\infty$ at ![]() $\delta =10$ to
$\delta =10$ to ![]() $\Delta t=0.005 R/v_\infty$ at
$\Delta t=0.005 R/v_\infty$ at ![]() $\delta =0.1$. The number of time steps to establish the steady-state flow is equal to
$\delta =0.1$. The number of time steps to establish the steady-state flow is equal to ![]() $N_{{steady}}=N_s/10$. The number of time steps for sampling the flow fields and sphere aerothermodynamic characteristics varies from
$N_{{steady}}=N_s/10$. The number of time steps for sampling the flow fields and sphere aerothermodynamic characteristics varies from ![]() $N_s=10^5$ at
$N_s=10^5$ at ![]() $Ma=1$ to
$Ma=1$ to ![]() $10^7$ at
$10^7$ at ![]() $Ma=0.1$.
$Ma=0.1$.
Table 2. Parameters of the numerical scheme.

5. Results and discussion
5.1. Effects of the gas species and interatomic potential
In the first series of simulations, the coefficients ![]() $C_D^*$ and
$C_D^*$ and ![]() $C_Q^*$ were calculated at
$C_Q^*$ were calculated at ![]() $T_w=T_\infty =300$ K assuming diffuse scattering on the sphere surface for all three noble gases (helium, neon and krypton) considered here. To reveal the effects of the interatomic potentials, additional simulations were also performed with the hard sphere (HS) molecular model. For the HS model,
$T_w=T_\infty =300$ K assuming diffuse scattering on the sphere surface for all three noble gases (helium, neon and krypton) considered here. To reveal the effects of the interatomic potentials, additional simulations were also performed with the hard sphere (HS) molecular model. For the HS model, ![]() $C_i^*=C_i^*(Ma,\delta,T_w/T_\infty,\alpha _t,\alpha _n)$
$C_i^*=C_i^*(Ma,\delta,T_w/T_\infty,\alpha _t,\alpha _n)$ ![]() $(i=p,f,h,D,Q)$ so that the results of simulations in the reduced units do not depend on the gas species if the model of diffuse scattering is used.
$(i=p,f,h,D,Q)$ so that the results of simulations in the reduced units do not depend on the gas species if the model of diffuse scattering is used.
The numerical values of the drag coefficient ![]() $C_D^*$ obtained by the DSMC method for helium are given in table 3. The second column in that table contains the limit values of
$C_D^*$ obtained by the DSMC method for helium are given in table 3. The second column in that table contains the limit values of ![]() $C_D^*$ at
$C_D^*$ at ![]() $Ma\to 0$ obtained by Kalempa & Sharipov (Reference Kalempa and Sharipov2020) at
$Ma\to 0$ obtained by Kalempa & Sharipov (Reference Kalempa and Sharipov2020) at ![]() $\delta =0.1$, 1 and 10. These limit values were obtained by the discrete velocity method applied to the linearized kinetic model proposed by Shakhov (Reference Shakhov1968). The limit values of
$\delta =0.1$, 1 and 10. These limit values were obtained by the discrete velocity method applied to the linearized kinetic model proposed by Shakhov (Reference Shakhov1968). The limit values of ![]() $C_D^*$ at
$C_D^*$ at ![]() $\delta =0.3$ and 3 are not available in the literature, so that the values of
$\delta =0.3$ and 3 are not available in the literature, so that the values of ![]() $C_D$ obtained by Takata, Sone & Aoki (Reference Takata, Sone and Aoki1993) applying the discrete velocity method to the linearized Boltzmann equation were interpolated to complete the second column of table 3. The analysis of the numerical results of
$C_D$ obtained by Takata, Sone & Aoki (Reference Takata, Sone and Aoki1993) applying the discrete velocity method to the linearized Boltzmann equation were interpolated to complete the second column of table 3. The analysis of the numerical results of ![]() $C_D^*$ for other gases and for the HS model showed that the effect of gas species on the drag coefficient
$C_D^*$ for other gases and for the HS model showed that the effect of gas species on the drag coefficient ![]() $C_D^*$ does not exceed a numerical error of 0.5 % so that these data are omitted here.
$C_D^*$ does not exceed a numerical error of 0.5 % so that these data are omitted here.
Table 3. Drag coefficient ![]() $C_D^*$ of helium versus Mach number
$C_D^*$ of helium versus Mach number ![]() $Ma$ and rarefaction parameter
$Ma$ and rarefaction parameter ![]() $\delta$ for diffuse scattering (
$\delta$ for diffuse scattering (![]() $\alpha _t=1$ and
$\alpha _t=1$ and ![]() $\alpha _n=1$) at
$\alpha _n=1$) at ![]() $T_\infty =T_w=300$ K. The values for
$T_\infty =T_w=300$ K. The values for ![]() $Ma\to 0$ are taken from Kalempa & Sharipov (Reference Kalempa and Sharipov2020) and Takata et al. (Reference Takata, Sone and Aoki1993). The values for
$Ma\to 0$ are taken from Kalempa & Sharipov (Reference Kalempa and Sharipov2020) and Takata et al. (Reference Takata, Sone and Aoki1993). The values for ![]() $Ma=1$ are taken from Sharipov & Volkov (Reference Sharipov and Volkov2022).
$Ma=1$ are taken from Sharipov & Volkov (Reference Sharipov and Volkov2022).

The results presented in table 3 show that the linear theory is applicable in a relatively large range of the Mach number when the rarefaction parameter is small. More specifically, when ![]() $\delta \le 1$, the values of
$\delta \le 1$, the values of ![]() $C_D^*$ obtained by the DSMC method at
$C_D^*$ obtained by the DSMC method at ![]() $Ma=0.1$ coincide with those obtained with the linear theory. However, the discrepancy between these two approaches becomes 7 % at
$Ma=0.1$ coincide with those obtained with the linear theory. However, the discrepancy between these two approaches becomes 7 % at ![]() $\delta =3$ and reaches 27 % at
$\delta =3$ and reaches 27 % at ![]() $\delta =10$. This trend is consistent with the analytical expressions (3.10) and (3.13).
$\delta =10$. This trend is consistent with the analytical expressions (3.10) and (3.13).
As mentioned above, the total energy flux ![]() $Q$ to the sphere used in the definition of
$Q$ to the sphere used in the definition of ![]() $C_Q^*$, equation (2.5), vanishes in the limit of
$C_Q^*$, equation (2.5), vanishes in the limit of ![]() $Ma\to 0$. More exactly, it exhibits asymptotic behaviour
$Ma\to 0$. More exactly, it exhibits asymptotic behaviour ![]() $Q\propto Ma^2$ when
$Q\propto Ma^2$ when ![]() $Ma\to 0$. This explains why an accurate calculation of
$Ma\to 0$. This explains why an accurate calculation of ![]() $C_Q^*$ at small
$C_Q^*$ at small ![]() $Ma$ is a difficult problem due to the statistical noise inherent for the DSMC method. As a result, it was not possible to reach a reasonable accuracy in calculation of
$Ma$ is a difficult problem due to the statistical noise inherent for the DSMC method. As a result, it was not possible to reach a reasonable accuracy in calculation of ![]() $C_Q^*$ at
$C_Q^*$ at ![]() $Ma=0.1$; therefore, the corresponding results are not shown here. The coefficient
$Ma=0.1$; therefore, the corresponding results are not shown here. The coefficient ![]() $C_Q^*$ for
$C_Q^*$ for ![]() $Ma=0.2$ and 0.5 for diffuse scattering and
$Ma=0.2$ and 0.5 for diffuse scattering and ![]() $T_w=T_\infty =300$ K is given in table 4 for the three noble gases and the HS model. Like
$T_w=T_\infty =300$ K is given in table 4 for the three noble gases and the HS model. Like ![]() $C_D^*$, the coefficient
$C_D^*$, the coefficient ![]() $C_Q^*$ is also weakly affected by the gas species, but the contribution of this factor is about 4 %, which exceeds the estimated numerical error of 1 %. According to (3.11), the contribution of the quadratic term (
$C_Q^*$ is also weakly affected by the gas species, but the contribution of this factor is about 4 %, which exceeds the estimated numerical error of 1 %. According to (3.11), the contribution of the quadratic term (![]() ${\sim }Ma^2$) to
${\sim }Ma^2$) to ![]() $C_Q^*$ in the free-molecular flow regime is about 4 % at
$C_Q^*$ in the free-molecular flow regime is about 4 % at ![]() ${Ma} =0.5$. A comparison of the values of
${Ma} =0.5$. A comparison of the values of ![]() $C_Q^*$ for
$C_Q^*$ for ![]() $Ma=0.2$ and
$Ma=0.2$ and ![]() $0.5$ in table 4 shows that the contribution of the quadratic term to
$0.5$ in table 4 shows that the contribution of the quadratic term to ![]() $C_Q^*$ remains within 4 % also for finite
$C_Q^*$ remains within 4 % also for finite ![]() $\delta$ in the range
$\delta$ in the range ![]() $0\le \delta\le 1$. This contribution increases for larger values of
$0\le \delta\le 1$. This contribution increases for larger values of ![]() $\delta$ and reaches 16 % at
$\delta$ and reaches 16 % at ![]() $\delta=10$. The contribution of the quadratic term to
$\delta=10$. The contribution of the quadratic term to ![]() $C_Q^*$ at
$C_Q^*$ at ![]() $Ma=0.2$ is expected to be equal to 0.7 % at
$Ma=0.2$ is expected to be equal to 0.7 % at ![]() $\delta\le 1$ and 2.5 % when
$\delta\le 1$ and 2.5 % when ![]() $1<\delta\le 10$. Based on these reasonings, the values of
$1<\delta\le 10$. Based on these reasonings, the values of ![]() $C_Q^*$ obtained for
$C_Q^*$ obtained for ![]() ${Ma} =0.2$ can be also used as a good approximation for
${Ma} =0.2$ can be also used as a good approximation for ![]() $C_Q^*$ at smaller
$C_Q^*$ at smaller ![]() $Ma$. The values of the average energy transfer coefficient for all gases considered in table 4 at
$Ma$. The values of the average energy transfer coefficient for all gases considered in table 4 at ![]() $Ma=1$ were obtained by Sharipov & Volkov (Reference Sharipov and Volkov2022).
$Ma=1$ were obtained by Sharipov & Volkov (Reference Sharipov and Volkov2022).
Table 4. Average energy transfer coefficient ![]() $C_Q^*$ versus Mach number
$C_Q^*$ versus Mach number ![]() $Ma$ and rarefaction parameter
$Ma$ and rarefaction parameter ![]() $\delta$ for diffuse scattering (
$\delta$ for diffuse scattering (![]() $\alpha _t=1$ and
$\alpha _t=1$ and ![]() $\alpha _n=1$) at
$\alpha _n=1$) at ![]() $T_\infty =T_w=300$ K.
$T_\infty =T_w=300$ K.

5.2. Effect of the surface accommodation coefficients
The values of the coefficients ![]() $C^*_D$ and
$C^*_D$ and ![]() $C^*_Q$ obtained for helium with sets (i) and (ii) of the accommodation coefficients, for neon with set (iii) and for krypton with diffuse scattering are compared in figure 2. The horizontal lines in these plots show the values of
$C^*_Q$ obtained for helium with sets (i) and (ii) of the accommodation coefficients, for neon with set (iii) and for krypton with diffuse scattering are compared in figure 2. The horizontal lines in these plots show the values of ![]() $C^*_D$ for free-molecular flows (
$C^*_D$ for free-molecular flows (![]() $\delta =0$) given in table 1 and
$\delta =0$) given in table 1 and ![]() $C^*_Q$ calculated from (3.11). Note that the difference in the values of
$C^*_Q$ calculated from (3.11). Note that the difference in the values of ![]() $C^*_D$ and
$C^*_D$ and ![]() $C^*_Q$ for different gases occurs only due to the different sets of accommodation coefficients. If the corresponding values of
$C^*_Q$ for different gases occurs only due to the different sets of accommodation coefficients. If the corresponding values of ![]() $C^*_D$ and
$C^*_D$ and ![]() $C^*_Q$ were to be plotted for the same parameters of the gas–surface interaction model, e.g. for the model of diffuse scattering, the curves for different gases would visually coincide in the scale of figure 2. Set (ii) leads to the largest values of the drag coefficient
$C^*_Q$ were to be plotted for the same parameters of the gas–surface interaction model, e.g. for the model of diffuse scattering, the curves for different gases would visually coincide in the scale of figure 2. Set (ii) leads to the largest values of the drag coefficient ![]() $C^*_D$, while set (i) corresponds to the smallest
$C^*_D$, while set (i) corresponds to the smallest ![]() $C^*_D$. Set (iii) represents a small deviation from the results obtained for diffuse scattering. In the near-continuum flow regime when
$C^*_D$. Set (iii) represents a small deviation from the results obtained for diffuse scattering. In the near-continuum flow regime when ![]() $\delta =10$, sets (ii) and (iii) result in practically the same values of
$\delta =10$, sets (ii) and (iii) result in practically the same values of ![]() $C_D^*$. The energy transfer coefficient
$C_D^*$. The energy transfer coefficient ![]() $C^*_Q$ is largest for diffuse scattering. This coefficient always decreases with decreasing either TMAC
$C^*_Q$ is largest for diffuse scattering. This coefficient always decreases with decreasing either TMAC ![]() $\alpha _t$ or NEAC
$\alpha _t$ or NEAC ![]() $\alpha _n$. The expression given by (3.11) shows that the coefficient
$\alpha _n$. The expression given by (3.11) shows that the coefficient ![]() $C^*_Q$ in the free-molecular flow regime is proportional to
$C^*_Q$ in the free-molecular flow regime is proportional to ![]() $\alpha _n+ \alpha _t(2-\alpha _t)$. This explains the largest value of
$\alpha _n+ \alpha _t(2-\alpha _t)$. This explains the largest value of ![]() $C^*_Q$ for diffuse scattering. The effect of the parameters of the gas–surface interaction model becomes weaker with approaching the continuum flow regime, when the rarefaction parameter
$C^*_Q$ for diffuse scattering. The effect of the parameters of the gas–surface interaction model becomes weaker with approaching the continuum flow regime, when the rarefaction parameter ![]() $\delta$ increases. The values of the drag and average energy transfer coefficients at
$\delta$ increases. The values of the drag and average energy transfer coefficients at ![]() $Ma=1$ were obtained by Sharipov & Volkov (Reference Sharipov and Volkov2022). These results reveal the same trends in the variation of
$Ma=1$ were obtained by Sharipov & Volkov (Reference Sharipov and Volkov2022). These results reveal the same trends in the variation of ![]() $C_D^*$ and
$C_D^*$ and ![]() $C_Q^*$ with
$C_Q^*$ with ![]() $\alpha _t$,
$\alpha _t$, ![]() $\alpha _n$ and
$\alpha _n$ and ![]() $\delta$ that are seen in figure 2(b,d) for
$\delta$ that are seen in figure 2(b,d) for ![]() $Ma=0.5$.
$Ma=0.5$.

Figure 2. Drag ![]() $C_D^*$ and average energy transfer
$C_D^*$ and average energy transfer ![]() $C_Q^*$ coefficients versus rarefaction parameter
$C_Q^*$ coefficients versus rarefaction parameter ![]() $\delta$ at
$\delta$ at ![]() $T_\infty = T_w = 300$ K for different sets of
$T_\infty = T_w = 300$ K for different sets of ![]() $\alpha _t$ and
$\alpha _t$ and ![]() $\alpha _n$: (a,c)
$\alpha _n$: (a,c) ![]() $Ma=0.2$; (b,d)
$Ma=0.2$; (b,d) ![]() $Ma=0.5$. The short horizontal lines correspond to the free-molecular flow regime.
$Ma=0.5$. The short horizontal lines correspond to the free-molecular flow regime.
The distributions of the local pressure ![]() $C_p^*$, friction
$C_p^*$, friction ![]() $C_f^*$ and energy transfer
$C_f^*$ and energy transfer ![]() $C_h^*$ coefficients for helium along the sphere surface obtained at
$C_h^*$ coefficients for helium along the sphere surface obtained at ![]() $Ma=0.2$ and
$Ma=0.2$ and ![]() $0.5$ when
$0.5$ when ![]() $T_w=T_\infty =300$ K with the model of diffuse scattering and with set (i) of the accommodation coefficients are compared in figure 3. To exclude statistical noise, which can be relatively large in the vicinity of the axis of symmetry, the distributions of parameters along the sphere surface in figure 3 and other figures were fitted by high-order polynomials using the least-squares method. The pressure coefficient
$T_w=T_\infty =300$ K with the model of diffuse scattering and with set (i) of the accommodation coefficients are compared in figure 3. To exclude statistical noise, which can be relatively large in the vicinity of the axis of symmetry, the distributions of parameters along the sphere surface in figure 3 and other figures were fitted by high-order polynomials using the least-squares method. The pressure coefficient ![]() $C_p^*$ is strongly sensitive to the accommodation coefficients at
$C_p^*$ is strongly sensitive to the accommodation coefficients at ![]() $\delta =0.1$ and 1, but is weakly sensitive at
$\delta =0.1$ and 1, but is weakly sensitive at ![]() $\delta =10.$ The friction
$\delta =10.$ The friction ![]() $C_f^*$ and energy transfer
$C_f^*$ and energy transfer ![]() $C_h^*$ coefficients are strongly sensitive to the values of the accommodation coefficients at all values of
$C_h^*$ coefficients are strongly sensitive to the values of the accommodation coefficients at all values of ![]() $\delta$ considered in figure 3; both
$\delta$ considered in figure 3; both ![]() $C_f^*$ and
$C_f^*$ and ![]() $C_h^*$ decrease when the accommodation coefficients
$C_h^*$ decrease when the accommodation coefficients ![]() $\alpha _t$ and
$\alpha _t$ and ![]() $\alpha _n$ decrease. Moreover, with a decrease in the values of accommodation coefficients, the distributions of
$\alpha _n$ decrease. Moreover, with a decrease in the values of accommodation coefficients, the distributions of ![]() $C_h^*$ qualitatively change. For diffuse scattering, the maximum of
$C_h^*$ qualitatively change. For diffuse scattering, the maximum of ![]() $C_h^*$ occurs in the forward stagnation point. At
$C_h^*$ occurs in the forward stagnation point. At ![]() $\alpha _t=0.4$ and
$\alpha _t=0.4$ and ![]() $\alpha _n=0.01$, the maximum of
$\alpha _n=0.01$, the maximum of ![]() $C_h^*$ is realized at
$C_h^*$ is realized at ![]() $\theta =90^\circ$, while the values of
$\theta =90^\circ$, while the values of ![]() $C_h^*$ are practically equal to zero in both stagnation points at
$C_h^*$ are practically equal to zero in both stagnation points at ![]() $\theta =0$ and
$\theta =0$ and ![]() $\theta =180^\circ$. In the case of non-diffuse scattering, the magnitude of
$\theta =180^\circ$. In the case of non-diffuse scattering, the magnitude of ![]() $C_h^*$ is significantly smaller than that for diffuse scattering.
$C_h^*$ is significantly smaller than that for diffuse scattering.

Figure 3. Pressure ![]() $C_p^*$, friction
$C_p^*$, friction ![]() $C_f^*$ and energy transfer
$C_f^*$ and energy transfer ![]() $C_h^*$ coefficients versus angle
$C_h^*$ coefficients versus angle ![]() $\theta$ at
$\theta$ at ![]() $T_\infty = T_w = 300$ K for helium at various
$T_\infty = T_w = 300$ K for helium at various ![]() $\delta$: (a,c,e)
$\delta$: (a,c,e) ![]() $Ma=0.2$; (b,d,f)
$Ma=0.2$; (b,d,f) ![]() $Ma=0.5$. Solid lines, diffuse scattering; dashed lines,
$Ma=0.5$. Solid lines, diffuse scattering; dashed lines, ![]() $\alpha _t$ = 0.4 and
$\alpha _t$ = 0.4 and ![]() $\alpha _n$ = 0.01.
$\alpha _n$ = 0.01.
It can be seen that the curves of ![]() $C_p^*$ and
$C_p^*$ and ![]() $C_f^*$ at
$C_f^*$ at ![]() $Ma=0.2$ are close to those at
$Ma=0.2$ are close to those at ![]() $Ma=0.5$ because both
$Ma=0.5$ because both ![]() $p_n-p_\infty$ and
$p_n-p_\infty$ and ![]() $\tau$, which define
$\tau$, which define ![]() $C_p$ and
$C_p$ and ![]() $C_f$ according to (2.3a–c), are proportional to
$C_f$ according to (2.3a–c), are proportional to ![]() $U_\infty$ at
$U_\infty$ at ![]() $Ma\to 0$. Therefore, both
$Ma\to 0$. Therefore, both ![]() $C_p^*$ and
$C_p^*$ and ![]() $C_f^*$ defined by (2.6) asymptotically vary as
$C_f^*$ defined by (2.6) asymptotically vary as ![]() $O(1)$ with respect to
$O(1)$ with respect to ![]() $Ma$ in the limit of
$Ma$ in the limit of ![]() $Ma\to 0$. However, the local energy flux
$Ma\to 0$. However, the local energy flux ![]() $J_e$, which defines
$J_e$, which defines ![]() $C_h$ in (2.3a–c), is proportional to
$C_h$ in (2.3a–c), is proportional to ![]() $U_\infty$ at
$U_\infty$ at ![]() $Ma\to 0$ like
$Ma\to 0$ like ![]() $p_n-p_\infty$ and
$p_n-p_\infty$ and ![]() $\tau$. As a result, the coefficient
$\tau$. As a result, the coefficient ![]() $C_h^*$ defined by (2.6) asymptotically varies as
$C_h^*$ defined by (2.6) asymptotically varies as ![]() $O(Ma^{-1})$ at
$O(Ma^{-1})$ at ![]() $Ma\to 0$ and, therefore, the quantity
$Ma\to 0$ and, therefore, the quantity ![]() $C_h^*$ at
$C_h^*$ at ![]() $Ma=0.2$ is substantially larger than that at
$Ma=0.2$ is substantially larger than that at ![]() $Ma=0.5$ as shown in figure 3.
$Ma=0.5$ as shown in figure 3.
In the case of diffuse scattering, the sphere is heated at its front part and cooled at its back part. Moreover, the function ![]() $C_h^*(\theta )$ becomes antisymmetric with respect to
$C_h^*(\theta )$ becomes antisymmetric with respect to ![]() $\theta =90^\circ$ at
$\theta =90^\circ$ at ![]() $Ma\to 0$. Such a behaviour of the local energy flux on the sphere surface in the limit of
$Ma\to 0$. Such a behaviour of the local energy flux on the sphere surface in the limit of ![]() $Ma\to 0$ was pointed out by Beresnev et al. (Reference Beresnev, Chernyak and Fomyagin1990) and by Kalempa & Sharipov (Reference Kalempa and Sharipov2020, Reference Kalempa and Sharipov2022). This phenomenon leads to the thermal polarization of a sphere when its thermal conductivity is small. Since the function
$Ma\to 0$ was pointed out by Beresnev et al. (Reference Beresnev, Chernyak and Fomyagin1990) and by Kalempa & Sharipov (Reference Kalempa and Sharipov2020, Reference Kalempa and Sharipov2022). This phenomenon leads to the thermal polarization of a sphere when its thermal conductivity is small. Since the function ![]() $C_h^*(\theta )$ becomes antisymmetric at
$C_h^*(\theta )$ becomes antisymmetric at ![]() $Ma\to 0$, the average energy flux coefficient
$Ma\to 0$, the average energy flux coefficient ![]() $C_Q^*$ is expected to asymptotically behave as
$C_Q^*$ is expected to asymptotically behave as ![]() $O(1)$ with respect to
$O(1)$ with respect to ![]() $Ma$, in agreement with the numerical results shown in figure 2.
$Ma$, in agreement with the numerical results shown in figure 2.
5.3. Effect of the sphere temperature
To study the effect of the surface temperature ![]() $T_w$ on the aerothermodynamics of a sphere, the DSMC simulations were performed at sphere temperature varying from
$T_w$ on the aerothermodynamics of a sphere, the DSMC simulations were performed at sphere temperature varying from ![]() $T_w=100$ to
$T_w=100$ to ![]() $1000$ K with the constant free-stream temperature equal to
$1000$ K with the constant free-stream temperature equal to ![]() $T_\infty =300$ K for helium interacting diffusely with the sphere surface. The values of the drag
$T_\infty =300$ K for helium interacting diffusely with the sphere surface. The values of the drag ![]() $C^*_D$ and average energy transfer
$C^*_D$ and average energy transfer ![]() $C^{**}_Q$ coefficients calculated for
$C^{**}_Q$ coefficients calculated for ![]() $Ma=0.1$,
$Ma=0.1$, ![]() $0.2$ and
$0.2$ and ![]() $0.5$ and various
$0.5$ and various ![]() $\delta$ are shown in figure 4. The drag coefficient
$\delta$ are shown in figure 4. The drag coefficient ![]() $C_D^*$ increases with increasing temperature
$C_D^*$ increases with increasing temperature ![]() $T_w$ for all Mach numbers and all rarefaction parameters
$T_w$ for all Mach numbers and all rarefaction parameters ![]() $\delta$. For all
$\delta$. For all ![]() $T_w$ considered, the values of
$T_w$ considered, the values of ![]() $C_D^*$ exhibit a weak dependence on
$C_D^*$ exhibit a weak dependence on ![]() $Ma$. As expected, the coefficient
$Ma$. As expected, the coefficient ![]() $C_Q^{**}$ practically linearly decreases with increasing temperature
$C_Q^{**}$ practically linearly decreases with increasing temperature ![]() $T_w$. The negative values of
$T_w$. The negative values of ![]() $C_Q^{**}$ mean that the energy is transferred from the sphere to the surrounding gas. The overall effect of
$C_Q^{**}$ mean that the energy is transferred from the sphere to the surrounding gas. The overall effect of ![]() $Ma$ on
$Ma$ on ![]() $C_Q^{**}$ is also weak. The adiabatic temperature of the sphere which corresponds to
$C_Q^{**}$ is also weak. The adiabatic temperature of the sphere which corresponds to ![]() $C_Q^{**}=0$ shifts towards larger values with increasing
$C_Q^{**}=0$ shifts towards larger values with increasing ![]() $Ma$.
$Ma$.

Figure 4. Drag ![]() $C_D^*$ and average energy transfer
$C_D^*$ and average energy transfer ![]() $C_Q^{**}$ coefficients of helium for diffuse scattering versus surface temperature
$C_Q^{**}$ coefficients of helium for diffuse scattering versus surface temperature ![]() $T_w$ for various
$T_w$ for various ![]() $Ma$ and
$Ma$ and ![]() $\delta$.
$\delta$.
The sphere temperature strongly affects the distributions of ![]() $C_p^*$ and
$C_p^*$ and ![]() $C_h^{**}$ as shown in figures 5 and 6 for
$C_h^{**}$ as shown in figures 5 and 6 for ![]() $Ma=0.2$ and
$Ma=0.2$ and ![]() $Ma=0.5$, respectively. An increase of
$Ma=0.5$, respectively. An increase of ![]() $T_w$ induces an increase of
$T_w$ induces an increase of ![]() $C_p^*$ at the whole sphere surface, so that the values of
$C_p^*$ at the whole sphere surface, so that the values of ![]() $C_p^*$ approach zero and can be even positive at
$C_p^*$ approach zero and can be even positive at ![]() $Ma=0.2$ in the downstream stagnation point,
$Ma=0.2$ in the downstream stagnation point, ![]() $\theta =180^\circ$. At
$\theta =180^\circ$. At ![]() $\delta =0.1$, the variation of
$\delta =0.1$, the variation of ![]() $C_p^*$ with
$C_p^*$ with ![]() $T_w$ is relatively large for the whole sphere surface. At
$T_w$ is relatively large for the whole sphere surface. At ![]() $\delta =10$, the effect of
$\delta =10$, the effect of ![]() $T_w$ on the distribution of
$T_w$ on the distribution of ![]() $C_p^*$ at the downstream-faced hemisphere becomes relatively weak. The overall effect of
$C_p^*$ at the downstream-faced hemisphere becomes relatively weak. The overall effect of ![]() $T_w$ on the distribution of
$T_w$ on the distribution of ![]() $C_p^*$ reduces with increasing
$C_p^*$ reduces with increasing ![]() $Ma$. As expected, the effect of
$Ma$. As expected, the effect of ![]() $T_w$ on
$T_w$ on ![]() $C_h^{**}$ is strong under all conditions considered. The distributions of the friction coefficient
$C_h^{**}$ is strong under all conditions considered. The distributions of the friction coefficient ![]() $C^*_f$ are weakly affected by
$C^*_f$ are weakly affected by ![]() $T_w$ and, therefore, not shown in figures 5 and 6.
$T_w$ and, therefore, not shown in figures 5 and 6.

Figure 5. Pressure ![]() $C_p^*$ and energy transfer
$C_p^*$ and energy transfer ![]() $C_h^{**}$ coefficients of helium for diffuse scattering versus angle
$C_h^{**}$ coefficients of helium for diffuse scattering versus angle ![]() $\theta$ for
$\theta$ for ![]() $Ma=0.2$ and various sphere temperatures
$Ma=0.2$ and various sphere temperatures ![]() $T_w$: (a,b)
$T_w$: (a,b) ![]() $\delta =0.1$; (c,d)
$\delta =0.1$; (c,d) ![]() $\delta =10$.
$\delta =10$.

Figure 6. Pressure ![]() $C_p^*$ and energy transfer
$C_p^*$ and energy transfer ![]() $C_h^{**}$ coefficients of helium for diffuse scattering versus angle
$C_h^{**}$ coefficients of helium for diffuse scattering versus angle ![]() $\theta$ for
$\theta$ for ![]() $Ma=0.5$ and various sphere temperatures
$Ma=0.5$ and various sphere temperatures ![]() $T_w$: (a,b)
$T_w$: (a,b) ![]() $\delta =0.1$; (c,d)
$\delta =0.1$; (c,d) ![]() $\delta =10$.
$\delta =10$.
In figure 7(a), the values of the drag coefficient obtained here by the DSMC method with diffuse scattering at ![]() $T_w=T_\infty$ are compared with the semi-empirical equations for
$T_w=T_\infty$ are compared with the semi-empirical equations for ![]() $C_D$ proposed by Henderson (Reference Henderson1976) and Loth et al. (Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021), which account for the effects of compressibility and rarefaction. The equation by Loth et al. (Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021) overall agrees well with the numerical values of
$C_D$ proposed by Henderson (Reference Henderson1976) and Loth et al. (Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021), which account for the effects of compressibility and rarefaction. The equation by Loth et al. (Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021) overall agrees well with the numerical values of ![]() $C_D$ in the whole range of
$C_D$ in the whole range of ![]() $\delta$ and
$\delta$ and ![]() $Ma$ considered in simulations, while the equation by Henderson (Reference Henderson1976) tends to overestimate
$Ma$ considered in simulations, while the equation by Henderson (Reference Henderson1976) tends to overestimate ![]() $C_D$ in the transitional and free-molecular flow regimes. The values of
$C_D$ in the transitional and free-molecular flow regimes. The values of ![]() $C_D$ obtained in the present work at
$C_D$ obtained in the present work at ![]() $T_w\not =T_\infty$ are compared with
$T_w\not =T_\infty$ are compared with ![]() $C_D$ calculated from the equation by Henderson (Reference Henderson1976) in figure 7(b). Note that the equation by Loth et al. (Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021) is obtained only for the case
$C_D$ calculated from the equation by Henderson (Reference Henderson1976) in figure 7(b). Note that the equation by Loth et al. (Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021) is obtained only for the case ![]() $T_w/T_\infty =1$. In contrast to the semi-empirical equation, the DSMC method predicts a non-negligible effect of
$T_w/T_\infty =1$. In contrast to the semi-empirical equation, the DSMC method predicts a non-negligible effect of ![]() $T_w/T_\infty$ on
$T_w/T_\infty$ on ![]() $C_D$ in the transitional and near-continuum regimes when
$C_D$ in the transitional and near-continuum regimes when ![]() $Re\sim 1$. At smaller
$Re\sim 1$. At smaller ![]() $Re$, the difference in
$Re$, the difference in ![]() $C_D$ between the semi-empirical equation and DSMC data points fast increases with increasing
$C_D$ between the semi-empirical equation and DSMC data points fast increases with increasing ![]() $T_w/T_\infty$. These results suggest that the equation by Henderson (Reference Henderson1976) can be used only at
$T_w/T_\infty$. These results suggest that the equation by Henderson (Reference Henderson1976) can be used only at ![]() $T_w/T_\infty \le 1$.
$T_w/T_\infty \le 1$.

Figure 7. Drag coefficient ![]() $C_D$ versus Reynolds number
$C_D$ versus Reynolds number ![]() $Re$ predicted by the semi-empirical equation of Henderson (Reference Henderson1976) (solid curves), the semi-empirical equation of Loth et al. (Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021) (dashed-dotted curves) and obtained in the present work (symbols and dashed curves): (a)
$Re$ predicted by the semi-empirical equation of Henderson (Reference Henderson1976) (solid curves), the semi-empirical equation of Loth et al. (Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021) (dashed-dotted curves) and obtained in the present work (symbols and dashed curves): (a) ![]() $T_w=T_\infty$ and various
$T_w=T_\infty$ and various ![]() $Ma$; (b)
$Ma$; (b) ![]() $Ma=0.1$ and various
$Ma=0.1$ and various ![]() $T_w$. The DSMC results correspond to helium with diffuse scattering at
$T_w$. The DSMC results correspond to helium with diffuse scattering at ![]() $T_\infty =300$ K.
$T_\infty =300$ K.
5.4. Flow fields
The fields of the gas density ![]() $n/n_\infty$, temperature
$n/n_\infty$, temperature ![]() $T/T_\infty$ and speed
$T/T_\infty$ and speed ![]() $u/U_\infty$ (
$u/U_\infty$ (![]() $u=|{\boldsymbol u}|$, where
$u=|{\boldsymbol u}|$, where ![]() ${\boldsymbol u}$ is the bulk velocity) with streamlines in the flow of helium over the sphere obtained with
${\boldsymbol u}$ is the bulk velocity) with streamlines in the flow of helium over the sphere obtained with ![]() $T_w=T_\infty =300$ K and diffuse scattering at
$T_w=T_\infty =300$ K and diffuse scattering at ![]() $Ma=0.2$ and
$Ma=0.2$ and ![]() $Ma=0.5$ are shown in figures 8 and 9, respectively. These fields are the typical subsonic flow fields over a thermally neutral sphere in the near-free-molecular (
$Ma=0.5$ are shown in figures 8 and 9, respectively. These fields are the typical subsonic flow fields over a thermally neutral sphere in the near-free-molecular (![]() $\delta =0.1$) and near-continuum (
$\delta =0.1$) and near-continuum (![]() $\delta =10$) flow regimes. All flow fields shown in figures 8 and 9 are characterized by the smooth variation of all quantities and by the propagation of the perturbations induced by the body to a long distance in the upstream direction. At
$\delta =10$) flow regimes. All flow fields shown in figures 8 and 9 are characterized by the smooth variation of all quantities and by the propagation of the perturbations induced by the body to a long distance in the upstream direction. At ![]() $Ma=0.2$ and
$Ma=0.2$ and ![]() $T_w/T_\infty =1$, the density and temperature fields indicate that the flows in this case are nearly incompressible and practically isothermal. The marginal variation of
$T_w/T_\infty =1$, the density and temperature fields indicate that the flows in this case are nearly incompressible and practically isothermal. The marginal variation of ![]() $T$ makes the accurate calculations of the temperature field and
$T$ makes the accurate calculations of the temperature field and ![]() $C_Q^*$ at
$C_Q^*$ at ![]() $Ma\le 0.2$ computationally challenging. At
$Ma\le 0.2$ computationally challenging. At ![]() $\delta =0.1$, the density and velocity fields visually are nearly symmetric with respect to the plane
$\delta =0.1$, the density and velocity fields visually are nearly symmetric with respect to the plane ![]() $x=0$. This qualitatively agrees with the linearized solution for the flow over a sphere at
$x=0$. This qualitatively agrees with the linearized solution for the flow over a sphere at ![]() $Ma\ll 1$ obtained by Kalempa & Sharipov (Reference Kalempa and Sharipov2020). With increasing
$Ma\ll 1$ obtained by Kalempa & Sharipov (Reference Kalempa and Sharipov2020). With increasing ![]() $\delta$, the flow field attains significant asymmetry with an extended wake behind the sphere.
$\delta$, the flow field attains significant asymmetry with an extended wake behind the sphere.

Figure 8. Fields of density ![]() $n/n_\infty$ (a,d), temperature
$n/n_\infty$ (a,d), temperature ![]() $T/T_\infty$ (b,e) and speed
$T/T_\infty$ (b,e) and speed ![]() $u/U_\infty$ with streamlines (c,f) for helium at
$u/U_\infty$ with streamlines (c,f) for helium at ![]() $Ma = 0.2$, diffuse scattering and
$Ma = 0.2$, diffuse scattering and ![]() $T_\infty = T_w = 300$ K: (a–c)
$T_\infty = T_w = 300$ K: (a–c) ![]() $\delta =0.1$; (d–f)
$\delta =0.1$; (d–f) ![]() $\delta =10$.
$\delta =10$.

Figure 9. Fields of density ![]() $n/n_\infty$ (a,d), temperature
$n/n_\infty$ (a,d), temperature ![]() $T/T_\infty$ (b,e) and speed
$T/T_\infty$ (b,e) and speed ![]() $u/U_\infty$ with streamlines (c,f) for helium at
$u/U_\infty$ with streamlines (c,f) for helium at ![]() $Ma = 0.5$, diffuse scattering and
$Ma = 0.5$, diffuse scattering and ![]() $T_\infty = T_w = 300$ K: (a–c)
$T_\infty = T_w = 300$ K: (a–c) ![]() $\delta =0.1$; (d–f)
$\delta =0.1$; (d–f) ![]() $\delta =10$.
$\delta =10$.
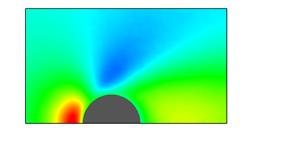
It is interesting that, in the subsonic flows at ![]() $Ma=0.2$ and 0.5, the maximum of gas temperature in the nearly continuum flow at
$Ma=0.2$ and 0.5, the maximum of gas temperature in the nearly continuum flow at ![]() $\delta =10$ is located inside the flow fields at the same point as where it is located in the supersonic flow at
$\delta =10$ is located inside the flow fields at the same point as where it is located in the supersonic flow at ![]() $Ma=2$, as reported previously by Sharipov & Volkov (Reference Sharipov and Volkov2022). At the axis of symmetry, the temperature maximum is realized at a distance of
$Ma=2$, as reported previously by Sharipov & Volkov (Reference Sharipov and Volkov2022). At the axis of symmetry, the temperature maximum is realized at a distance of ![]() $0.5R$ upstream from the stagnation point. Another local maximum of temperature is located at the axis of symmetry at a distance of
$0.5R$ upstream from the stagnation point. Another local maximum of temperature is located at the axis of symmetry at a distance of ![]() $x\approx 2.4R$ downstream the sphere. The temperature minimum is also located inside the flow field near the cross-section
$x\approx 2.4R$ downstream the sphere. The temperature minimum is also located inside the flow field near the cross-section ![]() $x=0$ at a distance of
$x=0$ at a distance of ![]() ${\approx }1.5R$ from the sphere centre. In comparison with the case of
${\approx }1.5R$ from the sphere centre. In comparison with the case of ![]() $Ma=0.2$, the flow at
$Ma=0.2$, the flow at ![]() $Ma=0.5$ is characterized by a significantly higher temperature in front of the sphere and deeper drop of the gas density behind it.
$Ma=0.5$ is characterized by a significantly higher temperature in front of the sphere and deeper drop of the gas density behind it.
The variation of the sphere surface temperature activates compressibility effects and can strongly affect the flow fields even in subsonic flows at small ![]() $Ma$. To illustrate this, the flow fields obtained at
$Ma$. To illustrate this, the flow fields obtained at ![]() $T_w=1000$ K and
$T_w=1000$ K and ![]() $Ma=0.2$ for
$Ma=0.2$ for ![]() $\delta =0.1$ and
$\delta =0.1$ and ![]() $10$ are shown in figure 10. These fields can be compared with the fields obtained under identical conditions but at
$10$ are shown in figure 10. These fields can be compared with the fields obtained under identical conditions but at ![]() $T_w=300$ K (figure 8). An increase in the surface temperature above
$T_w=300$ K (figure 8). An increase in the surface temperature above ![]() $T_\infty$ results in an increase of the gas temperature around the sphere and corresponding decrease in the gas number density, which is dictated by preserving gas pressure. The temperature-induced effects remain relatively small in magnitude in near-free-molecular flow at
$T_\infty$ results in an increase of the gas temperature around the sphere and corresponding decrease in the gas number density, which is dictated by preserving gas pressure. The temperature-induced effects remain relatively small in magnitude in near-free-molecular flow at ![]() $\delta =0.1$. In particular, the region of strong variation of the gas temperature is limited by the distances of
$\delta =0.1$. In particular, the region of strong variation of the gas temperature is limited by the distances of ![]() ${\approx }1.4R$ from the sphere centre and the velocity field retains approximate symmetry with respect to the plane
${\approx }1.4R$ from the sphere centre and the velocity field retains approximate symmetry with respect to the plane ![]() $x=0$. At
$x=0$. At ![]() $\delta =10$, the region with strong temperature variations extends far beyond in the downstream direction. The fields of
$\delta =10$, the region with strong temperature variations extends far beyond in the downstream direction. The fields of ![]() $n$ and
$n$ and ![]() $T$ tend to be spherically symmetric with decreasing
$T$ tend to be spherically symmetric with decreasing ![]() $Ma$, and, thus, qualitatively different from the corresponding fields at
$Ma$, and, thus, qualitatively different from the corresponding fields at ![]() $T_w=T_\infty$. With increasing
$T_w=T_\infty$. With increasing ![]() $T_w$, the disturbed field of gas velocity
$T_w$, the disturbed field of gas velocity ![]() $u$ becomes more extended in front of the sphere in the upstream direction so that the disturbances in the gas flow from the heated sphere propagate further than in the case of
$u$ becomes more extended in front of the sphere in the upstream direction so that the disturbances in the gas flow from the heated sphere propagate further than in the case of ![]() $T_w=T_\infty$. A decrease of
$T_w=T_\infty$. A decrease of ![]() $T_w$ with respect to
$T_w$ with respect to ![]() $T_\infty$ induces opposing changes in the flow field: a decrease of the gas temperature around the sphere, increase of the number density and less extended disturbed velocity field in front of the sphere (see the supplementary material).
$T_\infty$ induces opposing changes in the flow field: a decrease of the gas temperature around the sphere, increase of the number density and less extended disturbed velocity field in front of the sphere (see the supplementary material).

Figure 10. Fields of density ![]() $n/n_\infty$ (a,d), temperature
$n/n_\infty$ (a,d), temperature ![]() $T/T_\infty$ (b,e) and
$T/T_\infty$ (b,e) and ![]() $u/U_\infty$ with streamlines (c,f) for helium at
$u/U_\infty$ with streamlines (c,f) for helium at ![]() $Ma = 0.2$, diffuse scattering,
$Ma = 0.2$, diffuse scattering, ![]() $T_\infty = 300$ K and
$T_\infty = 300$ K and ![]() $T_w = 1000$ K: (a–c)
$T_w = 1000$ K: (a–c) ![]() $\delta =0.1$; (d–f)
$\delta =0.1$; (d–f) ![]() $\delta =10$.
$\delta =10$.
5.5. Stanton number, adiabatic sphere temperature and recovery factor
In compressible gas flows, the energy flux to the body surface is often represented in the dimensionless form by the Stanton number. For a sphere, the total energy flux ![]() $Q$ to its surface can be represented as
$Q$ to its surface can be represented as
where ![]() $St$ is the Stanton number and
$St$ is the Stanton number and ![]() $T_{ad}$ is the adiabatic sphere temperature, i.e. the homogeneous surface temperature, when the total energy flux from the surface is equal to zero. The relationship between
$T_{ad}$ is the adiabatic sphere temperature, i.e. the homogeneous surface temperature, when the total energy flux from the surface is equal to zero. The relationship between ![]() $C_Q$,
$C_Q$, ![]() $St$ and
$St$ and ![]() $T_{ad}/T_\infty$ is given by (2.5) and (5.1).
$T_{ad}/T_\infty$ is given by (2.5) and (5.1).
If the gas species, interatomic potential and accommodation coefficients of the Cercignani–Lampis gas–surface interaction model are fixed, then ![]() $T_{ad}/T_\infty$ is a function of
$T_{ad}/T_\infty$ is a function of ![]() $Ma$ and
$Ma$ and ![]() $\delta$, while
$\delta$, while ![]() $St$ depends on
$St$ depends on ![]() $Ma$,
$Ma$, ![]() $\delta$ and
$\delta$ and ![]() $T_w/T_\infty$. In the free-molecular regime for diffuse scattering,
$T_w/T_\infty$. In the free-molecular regime for diffuse scattering, ![]() $St$ is given by the equation
$St$ is given by the equation
where ![]() $S=U_\infty /v_\infty =\sqrt {10/3}Ma$. The ratio
$S=U_\infty /v_\infty =\sqrt {10/3}Ma$. The ratio ![]() $T_{ad}/T_\infty$ can be represented in the form
$T_{ad}/T_\infty$ can be represented in the form
where ![]() $\zeta$ is the recovery factor defined as
$\zeta$ is the recovery factor defined as
and ![]() $T_0=T_\infty [1+(2/5)S^2]$ is the isentropic stagnation temperature. The dimensionless recovery factor is a measure of the difference of the adiabatic body temperature from the isentropic stagnation temperature. This difference depends on the efficiency of collisional equilibration of gas molecules moving to and from the body surface. The value of
$T_0=T_\infty [1+(2/5)S^2]$ is the isentropic stagnation temperature. The dimensionless recovery factor is a measure of the difference of the adiabatic body temperature from the isentropic stagnation temperature. This difference depends on the efficiency of collisional equilibration of gas molecules moving to and from the body surface. The value of ![]() $\zeta$ can be considered as another integral measure of the degree of gas rarefaction in the rarefied gas aerodynamics as it varies for bodies of various shapes from values larger than 1 in free-molecular flows to values smaller than 1 in continuum flows. In the free-molecular regime, the recovery factor for a sphere takes the form
$\zeta$ can be considered as another integral measure of the degree of gas rarefaction in the rarefied gas aerodynamics as it varies for bodies of various shapes from values larger than 1 in free-molecular flows to values smaller than 1 in continuum flows. In the free-molecular regime, the recovery factor for a sphere takes the form
At finite ![]() $\delta$, the dependence of
$\delta$, the dependence of ![]() $C_Q^\ast$ on multiple flow parameters is relatively complex. The analysis of
$C_Q^\ast$ on multiple flow parameters is relatively complex. The analysis of ![]() $T_{ad}/T_\infty$ and
$T_{ad}/T_\infty$ and ![]() $St$ allows one to reveal universal trends that control the variation of
$St$ allows one to reveal universal trends that control the variation of ![]() $C_Q$ as a function of multiple flow parameters. For this purpose, the values of
$C_Q$ as a function of multiple flow parameters. For this purpose, the values of ![]() $C_Q^\ast$ obtained with the DSMC method for helium and shown in figure 4 are recalculated into the values of
$C_Q^\ast$ obtained with the DSMC method for helium and shown in figure 4 are recalculated into the values of ![]() $St$ and
$St$ and ![]() $T_{ad}/T_\infty$.
$T_{ad}/T_\infty$.
The values of ![]() $T_{ad}$ are determined first as the surface temperatures when
$T_{ad}$ are determined first as the surface temperatures when ![]() $Q=0$. Since the variation of
$Q=0$. Since the variation of ![]() $C_Q^{**}$ with
$C_Q^{**}$ with ![]() $T_w$ is practically linear (figure 4),
$T_w$ is practically linear (figure 4), ![]() $T_{ad}$ can be obtained by the linear interpolation of
$T_{ad}$ can be obtained by the linear interpolation of ![]() $C_Q^{\ast \ast }$ between two points corresponding to temperatures
$C_Q^{\ast \ast }$ between two points corresponding to temperatures ![]() $T_{w(1)}$ and
$T_{w(1)}$ and ![]() $T_{w(2)}$:
$T_{w(2)}$:
 \begin{equation} T_{ad} = \frac{T_{w(1)} C_{Q(2)}^{{\ast}{\ast}} - T_{w(1)} C_{Q(1)}^{{\ast}{\ast}}}{C_{Q(2)}^{{\ast}{\ast}} - C_{Q(1)}^{{\ast}{\ast}} },\end{equation}
\begin{equation} T_{ad} = \frac{T_{w(1)} C_{Q(2)}^{{\ast}{\ast}} - T_{w(1)} C_{Q(1)}^{{\ast}{\ast}}}{C_{Q(2)}^{{\ast}{\ast}} - C_{Q(1)}^{{\ast}{\ast}} },\end{equation}
where ![]() $C_{Q(k)}^{\ast \ast }$ is the average energy transfer coefficient obtained at
$C_{Q(k)}^{\ast \ast }$ is the average energy transfer coefficient obtained at ![]() $T_w=T_{w(k)}$ and
$T_w=T_{w(k)}$ and ![]() $C_{Q(1)}^{\ast \ast } \times C_{Q(2)}^{\ast \ast } < 0$. Since
$C_{Q(1)}^{\ast \ast } \times C_{Q(2)}^{\ast \ast } < 0$. Since ![]() $T_{ad} / T_\infty > 1$ and, for
$T_{ad} / T_\infty > 1$ and, for ![]() $Ma\le 1$,
$Ma\le 1$, ![]() $T_{ad} / T_\infty < 2$, (5.6) is used at
$T_{ad} / T_\infty < 2$, (5.6) is used at ![]() $T_{w(1)}=300$ K and
$T_{w(1)}=300$ K and ![]() $T_{w(2)}=600$ K. The obtained raw values of
$T_{w(2)}=600$ K. The obtained raw values of ![]() $\Delta T_{ad}=T_{ad} / T_\infty - 1$ are shown in figure 11(a). These results indicate a monotonic decrease of
$\Delta T_{ad}=T_{ad} / T_\infty - 1$ are shown in figure 11(a). These results indicate a monotonic decrease of ![]() $\Delta T_{ad}$ with
$\Delta T_{ad}$ with ![]() $\delta$ and increase with
$\delta$ and increase with ![]() $Ma$. In the transitional regime, the magnitude of
$Ma$. In the transitional regime, the magnitude of ![]() $\Delta T_{ad}$ varies roughly inversely proportional to
$\Delta T_{ad}$ varies roughly inversely proportional to ![]() $Ma^2$ in agreement with (5.3) for the free-molecular regime. The numerical values of
$Ma^2$ in agreement with (5.3) for the free-molecular regime. The numerical values of ![]() $T_{ad}/T_\infty$ are compared with the predictions based on the semi-empirical equation proposed by Koshmarov & Svirshevskii (Reference Koshmarov and Svirshevskii1993) to describe the adiabatic temperature of a sphere under a broad range of conditions, including the free-molecular, transitional and continuum flow regimes, in the supplementary material. This comparison showed that the semi-empirical equation systematically overestimates
$T_{ad}/T_\infty$ are compared with the predictions based on the semi-empirical equation proposed by Koshmarov & Svirshevskii (Reference Koshmarov and Svirshevskii1993) to describe the adiabatic temperature of a sphere under a broad range of conditions, including the free-molecular, transitional and continuum flow regimes, in the supplementary material. This comparison showed that the semi-empirical equation systematically overestimates ![]() $T_{ad}/T_\infty$ compared with the DSMC results.
$T_{ad}/T_\infty$ compared with the DSMC results.

Figure 11. Values of ![]() $\Delta T_{ad}= T_{ad} / T_\infty - 1$ (a), recovery factor
$\Delta T_{ad}= T_{ad} / T_\infty - 1$ (a), recovery factor ![]() $\zeta$ (b) and
$\zeta$ (b) and ![]() $St \cdot Ma$ (c–e) versus density parameter
$St \cdot Ma$ (c–e) versus density parameter ![]() $\delta$ at various
$\delta$ at various ![]() $Ma$ and
$Ma$ and ![]() $T_w$ obtained for helium with diffuse scattering. In (b), horizontal arrows mark the values of
$T_w$ obtained for helium with diffuse scattering. In (b), horizontal arrows mark the values of ![]() $\zeta$ in the free-molecular regime at
$\zeta$ in the free-molecular regime at ![]() $Ma=0.1$ and
$Ma=0.1$ and ![]() $Ma=1$.
$Ma=1$.
The recovery factor for a monatomic gas ![]() $\zeta =3( T_{ad} / T_\infty - 1 ) / Ma^2$ obtained from (5.4) demonstrates a universal behaviour and only weakly depends on
$\zeta =3( T_{ad} / T_\infty - 1 ) / Ma^2$ obtained from (5.4) demonstrates a universal behaviour and only weakly depends on ![]() $Ma$ as shown in figure 11(b). Under conditions of nearly free-molecular regime at
$Ma$ as shown in figure 11(b). Under conditions of nearly free-molecular regime at ![]() $\delta =0.1$,
$\delta =0.1$, ![]() $\zeta$ decreases when
$\zeta$ decreases when ![]() $Ma$ increases from
$Ma$ increases from ![]() $0.2$ to
$0.2$ to ![]() $1$ in agreement with (5.5) for the free-molecular regime which predicts the values of
$1$ in agreement with (5.5) for the free-molecular regime which predicts the values of ![]() $\zeta =1.665$,
$\zeta =1.665$, ![]() $1.659$,
$1.659$, ![]() $1.625$ and
$1.625$ and ![]() $1.535$ for
$1.535$ for ![]() $Ma=0.1$,
$Ma=0.1$, ![]() $0.2$,
$0.2$, ![]() $0.5$ and
$0.5$ and ![]() $1$, respectively. On the contrary, in the near-continuum regime at
$1$, respectively. On the contrary, in the near-continuum regime at ![]() $\delta =10$,
$\delta =10$, ![]() $\zeta$ increases when
$\zeta$ increases when ![]() $Ma$ increases from
$Ma$ increases from ![]() $0.2$ to
$0.2$ to ![]() $1$. A density parameter of
$1$. A density parameter of ![]() $\delta \approx 0.5$ corresponds to the nexus point where
$\delta \approx 0.5$ corresponds to the nexus point where ![]() $\zeta$ does not change with
$\zeta$ does not change with ![]() $Ma$. The values of
$Ma$. The values of ![]() $\zeta$ at
$\zeta$ at ![]() $Ma=0.1$ are out of these trends presumably due to insufficient accuracy of DSMC simulations in this case.
$Ma=0.1$ are out of these trends presumably due to insufficient accuracy of DSMC simulations in this case.
Once the numerical values of ![]() $T_{ad} / T_\infty$ are determined, the values of
$T_{ad} / T_\infty$ are determined, the values of ![]() $St$ can be calculated as
$St$ can be calculated as
 \begin{equation} St = \frac{\gamma - 1 }{2 } \frac{C_Q^{{\ast}{\ast}}}{Ma \left(\dfrac{ T_{ad} } { T_\infty } - \dfrac{ T_w } { T_\infty } \right) }.\end{equation}
\begin{equation} St = \frac{\gamma - 1 }{2 } \frac{C_Q^{{\ast}{\ast}}}{Ma \left(\dfrac{ T_{ad} } { T_\infty } - \dfrac{ T_w } { T_\infty } \right) }.\end{equation}
A table with the calculated values of ![]() $T_{ad}/T_\infty$ and
$T_{ad}/T_\infty$ and ![]() $St$ is provided in the supplementary material. Since
$St$ is provided in the supplementary material. Since ![]() $C_Q^{\ast \ast }$ weakly depends on
$C_Q^{\ast \ast }$ weakly depends on ![]() $Ma$, it is expected that
$Ma$, it is expected that ![]() $St \cdot Ma$ is a weak function of
$St \cdot Ma$ is a weak function of ![]() $Ma$ as well. The dependencies of
$Ma$ as well. The dependencies of ![]() $St \cdot Ma$ on
$St \cdot Ma$ on ![]() $\delta$ at various
$\delta$ at various ![]() $Ma$ and
$Ma$ and ![]() $T_w/T_\infty$ are shown in figure 11(c–e). In the limit of the free-molecular regime,
$T_w/T_\infty$ are shown in figure 11(c–e). In the limit of the free-molecular regime, ![]() $St \cdot Ma$ becomes independent of
$St \cdot Ma$ becomes independent of ![]() $T_w/T_\infty$ according to (5.2). In the transitional regime at
$T_w/T_\infty$ according to (5.2). In the transitional regime at ![]() $\delta <3$, the calculated values of
$\delta <3$, the calculated values of ![]() $St \cdot Ma$ demonstrate a weak dependence on
$St \cdot Ma$ demonstrate a weak dependence on ![]() $Ma$ and
$Ma$ and ![]() $T_w/T_\infty$. In the near-continuum regime at
$T_w/T_\infty$. In the near-continuum regime at ![]() $\delta \sim 10$, the effect of
$\delta \sim 10$, the effect of ![]() $T_w$ becomes relatively strong at small
$T_w$ becomes relatively strong at small ![]() $Ma=0.1$ and
$Ma=0.1$ and ![]() $0.2$.
$0.2$.
Thus, the variation of both ![]() $\zeta$ and
$\zeta$ and ![]() $St \cdot Ma$ is dominated only by
$St \cdot Ma$ is dominated only by ![]() $\delta$. This fact simplifies the development of the fitting equations for prediction of the average energy transfer coefficient of a sphere under a broad range of conditions. It was already used in the development of the semi-empirical equation for the Nusselt number
$\delta$. This fact simplifies the development of the fitting equations for prediction of the average energy transfer coefficient of a sphere under a broad range of conditions. It was already used in the development of the semi-empirical equation for the Nusselt number ![]() $Nu$ by Kavanau (Reference Kavanau1955). This equation was proposed in the form
$Nu$ by Kavanau (Reference Kavanau1955). This equation was proposed in the form
 \begin{equation} Nu = \frac{ Nu_c} {1 + 3.42 \dfrac{ Ma } {Pr \ Re } Nu_c },\end{equation}
\begin{equation} Nu = \frac{ Nu_c} {1 + 3.42 \dfrac{ Ma } {Pr \ Re } Nu_c },\end{equation}
where ![]() $Nu_c=Nu_c(Re, Pr)$ is the value of the sphere Nusselt number in the continuum flow regime,
$Nu_c=Nu_c(Re, Pr)$ is the value of the sphere Nusselt number in the continuum flow regime, ![]() $Pr$ is the Prandtl number, which is nearly constant for monatomic gases,
$Pr$ is the Prandtl number, which is nearly constant for monatomic gases, ![]() $Pr\approx 0.67$, and the effects of rarefaction are determined by the parameter
$Pr\approx 0.67$, and the effects of rarefaction are determined by the parameter ![]() $Pr Re /Ma \sim Pr \delta$. Equation (5.8) is designed to fit the experimental data for the sphere Nusselt number at
$Pr Re /Ma \sim Pr \delta$. Equation (5.8) is designed to fit the experimental data for the sphere Nusselt number at ![]() $0.1\le Ma \le 0.69$ and
$0.1\le Ma \le 0.69$ and ![]() $1.75\le Re\le 124$. In this equation,
$1.75\le Re\le 124$. In this equation, ![]() $Nu_c$ can be calculated, for example, with the equation (Eckert & Drake Reference Eckert and Drake1959)
$Nu_c$ can be calculated, for example, with the equation (Eckert & Drake Reference Eckert and Drake1959)
as suggested by Nelson & Fields (Reference Nelson and Fields1996).
The numerical values of ![]() $St$ calculated for
$St$ calculated for ![]() $T_w=T_\infty$ are compared with
$T_w=T_\infty$ are compared with ![]() $St=Nu/(Pr Re)$ defined by (5.8) in figure 12. The semi-empirical equation by Kavanau (Reference Kavanau1955) agrees well with the DSMC data points at
$St=Nu/(Pr Re)$ defined by (5.8) in figure 12. The semi-empirical equation by Kavanau (Reference Kavanau1955) agrees well with the DSMC data points at ![]() $Re\ge 1$ in the whole range of the Mach number considered here. At smaller
$Re\ge 1$ in the whole range of the Mach number considered here. At smaller ![]() $Re$, this equation overestimates the Stanton number at
$Re$, this equation overestimates the Stanton number at ![]() $Ma=0.1$,
$Ma=0.1$, ![]() $0.2$ and
$0.2$ and ![]() $0.5$, while it somewhat underestimates
$0.5$, while it somewhat underestimates ![]() $St$ at
$St$ at ![]() $Ma=1$ since this equation cannot predict the correct asymptotic behaviour of
$Ma=1$ since this equation cannot predict the correct asymptotic behaviour of ![]() $St$ in the free-molecular flow regime when
$St$ in the free-molecular flow regime when ![]() $Re\rightarrow 0$ at
$Re\rightarrow 0$ at ![]() $Ma=const$. Good agreement between the DSMC data points and semi-empirical equation at
$Ma=const$. Good agreement between the DSMC data points and semi-empirical equation at ![]() $Ma=1$ suggests that the Kavanau (Reference Kavanau1955) equation can be used to predict the value of
$Ma=1$ suggests that the Kavanau (Reference Kavanau1955) equation can be used to predict the value of ![]() $St$ up to
$St$ up to ![]() $Ma=1$ in the transitional and continuum regimes at
$Ma=1$ in the transitional and continuum regimes at ![]() $Re\ge 1$. At relatively large subsonic
$Re\ge 1$. At relatively large subsonic ![]() $Ma$, however, the deviations of
$Ma$, however, the deviations of ![]() $T_{ad}/T_\infty$ from 1 become substantial (see figure 11a) so that the calculations of the total energy flux
$T_{ad}/T_\infty$ from 1 become substantial (see figure 11a) so that the calculations of the total energy flux ![]() $Q$ require accurate equations for both
$Q$ require accurate equations for both ![]() $St$ and
$St$ and ![]() $T_{ad}/T_\infty$.
$T_{ad}/T_\infty$.

Figure 12. Stanton number ![]() $St$ versus Reynolds number
$St$ versus Reynolds number ![]() $Re$ based on the Kavanau equation (5.8) (solid curves) and obtained with the DSMC method (symbols with dashed curves) at various
$Re$ based on the Kavanau equation (5.8) (solid curves) and obtained with the DSMC method (symbols with dashed curves) at various ![]() $Ma$ and
$Ma$ and ![]() $T_w=300$ K for helium with diffuse scattering.
$T_w=300$ K for helium with diffuse scattering.
6. Conclusions
The aerothermodynamic characteristics of a sphere in subsonic flows were calculated by the DSMC method employing ab initio potentials for interatomic collisions and the HS molecular model. The calculations were performed for the noble gases helium, neon and krypton over a wide range of gas rarefaction spanning the free-molecular, transitional and continuum regimes for Mach number equal to 0.1, 0.2, 0.5 and 1. The Cercignani–Lampis kernel for gas–surface interaction was used to describe non-diffuse scattering. The parameters of the numerical scheme were chosen to provide numerical errors in the drag coefficient less than 0.5 % at ![]() ${Ma} \ge 0.1$ and in the average energy transfer coefficient less than 1 % at
${Ma} \ge 0.1$ and in the average energy transfer coefficient less than 1 % at ![]() ${Ma} \ge 0.2$. The effects of several factors, such as gas species, sphere surface temperature and accommodation coefficients, on the flow fields as well as sphere drag and average energy transfer coefficients were studied. The calculated values of the average energy transfer coefficient were used to find the Stanton number and adiabatic temperature of the sphere. The analysis of the numerical results leads to the following conclusions:
${Ma} \ge 0.2$. The effects of several factors, such as gas species, sphere surface temperature and accommodation coefficients, on the flow fields as well as sphere drag and average energy transfer coefficients were studied. The calculated values of the average energy transfer coefficient were used to find the Stanton number and adiabatic temperature of the sphere. The analysis of the numerical results leads to the following conclusions:
(i) In subsonic flows, the aerothermodynamic characteristics of the sphere based on the ab initio potentials are close to those based on the HS model if the same parameters of the gas–surface interaction model are used. Thus, the sphere drag and heat transfer in subsonic flows are nearly independent of the gas species but dominated by the parameters of gas scattering at the body surface.
(ii) In the transitional and free-molecular regimes (
 $\delta \le 1$), the drag coefficient at
$\delta \le 1$), the drag coefficient at  $Ma=0.1$ is close to that obtained from the linearized kinetic equation. In the near-continuum regime (
$Ma=0.1$ is close to that obtained from the linearized kinetic equation. In the near-continuum regime ( $\delta =10$), the difference between the DSMC solutions and linear theory is significant at all values of
$\delta =10$), the difference between the DSMC solutions and linear theory is significant at all values of  $Ma$ considered.
$Ma$ considered.(iii) The values of the drag and average heat transfer coefficients are strongly sensitive to the accommodation coefficients in the Cercignani–Lampis scattering kernel. The diffuse gas–surface interaction always leads to the largest value of the energy transfer coefficient in comparison with non-diffuse interaction. The drag coefficient exhibits a complex behaviour as a function of the accommodation coefficients. It can be either larger or smaller than the drag coefficient in the case of diffuse scattering. Such a behaviour is predicted by both the DSMC method in the transitional regime and theoretical equations obtained for free-molecular flows.
(iv) Both the DSMC method and theoretical solution for the free-molecular regime show that the drag coefficient increases with increasing sphere surface temperature when the free-stream temperature is constant. The average heat transfer coefficient decreases almost linearly with increasing temperature of the sphere.
(v) The Stanton number and adiabatic sphere temperature, which determine the average energy transfer coefficient of the sphere, after appropriate scaling, exhibit weak dependence on the Mach number and relative sphere temperature. Thus, they demonstrate universal scaling behaviours as functions of the density parameter. This finding may result in the development of a relatively simple fitting equation for the average heat transfer coefficient as a function of all flow parameters.
(vi) In the case of diffuse scattering, the values of the drag coefficient found by the DSMC method when the sphere temperature is equal to the free-stream temperate are in good quantitative agreement with the fitting equation proposed by Loth et al. (Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021). The fitting equation developed by Henderson (Reference Henderson1976) overestimates the drag coefficient in the transitional and near-free-molecular regimes, and the degree of overestimation increases with increasing surface temperature. The fitting equation proposed by Kavanau (Reference Kavanau1955) for the sphere Nusselt number agrees with the results of the DSMC method when the Reynolds number is greater than 1. At smaller Reynolds numbers, this equation substantially overestimates the DSMC results.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2024.1036.
Acknowledgements
F.S. thanks CNPq, Brazil for the support of his research (grant no. 303429/2022-4). A.N.V. acknowledges the support of the present work by the National Science Foundation (USA) through RII-Track-1 Future Technologies and Enabling Plasma Processes project (award OIA-2148653). Computational support is provided by the Alabama Supercomputer Center and Laboratório Central de Processamento de Alto Desempenho of UFPR.
Declaration of interests
The authors report no conflict of interest.