Published online by Cambridge University Press: 03 March 2022
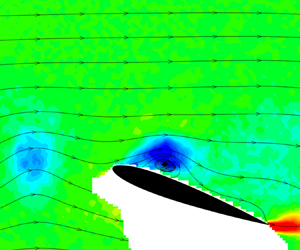
The aerodynamics of a stationary wing in a turbulent wake are investigated. Force and velocity measurements are used to describe the unsteady flow. Various wakes are studied with different dominant frequencies and length scales. In contrast to the pre-stall angles of attack, the time-averaged lift increases substantially at post-stall angles of attack as the wing interacts with the von Kármán vortex street and experiences temporal variations of the effective angle of attack. At an optimal offset distance from the wake centreline, the time-averaged lift becomes maximum despite of small amplitude oscillations in the effective angle of attack. The stall angle of attack can reach 20° and the maximum lift coefficient can reach 64 % higher than that in the freestream. Whereas large velocity fluctuations at the wake centreline cause excursions into the fully attached and separated flows during the cycle, small-amplitude oscillations at the optimal location result in periodic shedding of leading edge vortices. These vortices may produce large separation bubbles with reattachment near the trailing-edge. Vorticity roll-up, strength and size of the vortices increase with increasing wavelength and period of the von Kármán vortex street, which also coincides with an increase in the spanwise length scale of the incident wake, and all contribute to the remarkable increase in lift.