Article contents
Adjoint sensitivity and optimal perturbations of the low-speed jet in cross-flow
Published online by Cambridge University Press: 22 August 2019
Abstract
The tri-global stability and sensitivity of the low-speed jet in cross-flow are studied using the adjoint equations and finite-time horizon optimal disturbance analysis at Reynolds number 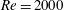 $Re=2000$, based on the average velocity at the jet exit, the jet nozzle exit diameter and the kinematic viscosity of the jet, for two jet-to-cross-flow velocity ratios
$Re=2000$, based on the average velocity at the jet exit, the jet nozzle exit diameter and the kinematic viscosity of the jet, for two jet-to-cross-flow velocity ratios 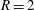 $R=2$ and
$R=2$ and 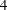 $4$. A novel capability is developed on unstructured grids and parallel platforms for this purpose. Asymmetric modes are more important to the overall dynamics at
$4$. A novel capability is developed on unstructured grids and parallel platforms for this purpose. Asymmetric modes are more important to the overall dynamics at 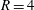 $R=4$, suggesting increased sensitivity to experimental asymmetries at higher
$R=4$, suggesting increased sensitivity to experimental asymmetries at higher 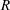 $R$. Low-frequency modes show a connection to wake vortices. Adjoint modes show that the upstream shear layer is most sensitive to perturbations along the upstream side of the jet nozzle. Lower frequency downstream modes are sensitive in the cross-flow boundary layer. For
$R$. Low-frequency modes show a connection to wake vortices. Adjoint modes show that the upstream shear layer is most sensitive to perturbations along the upstream side of the jet nozzle. Lower frequency downstream modes are sensitive in the cross-flow boundary layer. For 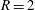 $R=2$, optimal analysis reveals that for short time horizons, asymmetric perturbations dominate and grow along the counter-rotating vortex pair observed in the cross-section. However, as the time horizon increases, large transient growth is observed along the upstream shear layer. When
$R=2$, optimal analysis reveals that for short time horizons, asymmetric perturbations dominate and grow along the counter-rotating vortex pair observed in the cross-section. However, as the time horizon increases, large transient growth is observed along the upstream shear layer. When 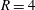 $R=4$, the optimal perturbations for short time scales grow along the downstream shear layer. For long time horizons, they become hybrid modes that grow along both the upstream and downstream shear layers.
$R=4$, the optimal perturbations for short time scales grow along the downstream shear layer. For long time horizons, they become hybrid modes that grow along both the upstream and downstream shear layers.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
Footnotes
Present address: 110 Union Street SE, 107 Akerman Hall, Minneapolis, MN 55455, USA. Email address for correspondence: [email protected]
References
- 8
- Cited by


