Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Clamond, Didier
2017.
Remarks on Bernoulli constants, gauge conditions and phase velocities in the context of water waves.
Applied Mathematics Letters,
Vol. 74,
Issue. ,
p.
114.
Clamond, Didier
2018.
New exact relations for steady irrotational two-dimensional gravity and capillary surface waves.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 376,
Issue. 2111,
p.
20170220.
Le, Uyen
and
Pelinovsky, Dmitry E.
2019.
Convergence of Petviashvili's Method near Periodic Waves in the Fractional Korteweg--de Vries Equation.
SIAM Journal on Mathematical Analysis,
Vol. 51,
Issue. 4,
p.
2850.
Kuznetsov, Nikolay
and
Dinvay, Evgueni
2019.
Babenko’s Equation for Periodic Gravity Waves on Water of Finite Depth: Derivation and Numerical Solution.
Water Waves,
Vol. 1,
Issue. 1,
p.
41.
Papathanasiou, T. K.
Papoutsellis, Ch. E.
and
Athanassoulis, G. A.
2019.
Semi-explicit solutions to the water-wave dispersion relation and their role in the non-linear Hamiltonian coupled-mode theory.
Journal of Engineering Mathematics,
Vol. 114,
Issue. 1,
p.
87.
Dinvay, E
and
Kuznetsov, N
2019.
Modified Babenko’s Equation For Periodic Gravity Waves On Water Of Finite Depth.
The Quarterly Journal of Mechanics and Applied Mathematics,
Vol. 72,
Issue. 4,
p.
415.
Fouques, Sébastien
and
Pákozdi, Csaba
2020.
A mixed Eulerian-Lagrangian High-Order Spectral method for the propagation of ocean surface waves over a flat bottom.
Journal of Computational Physics: X,
Vol. 8,
Issue. ,
p.
100071.
Klahn, Mathias
Madsen, Per A.
and
Fuhrman, David R.
2020.
On the accuracy and applicability of a new implicit Taylor method and the high-order spectral method on steady nonlinear waves.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 476,
Issue. 2243,
Klahn, Mathias
Madsen, Per A.
and
Fuhrman, David R.
2021.
Simulation of three‐dimensional nonlinear water waves using a pseudospectral volumetric method with an artificial boundary condition.
International Journal for Numerical Methods in Fluids,
Vol. 93,
Issue. 6,
p.
1843.
Chen, Lin
Basu, Biswajit
and
Martin, Calin-I.
2021.
On rotational flows with discontinuous vorticity beneath steady water waves near stagnation.
Journal of Fluid Mechanics,
Vol. 912,
Issue. ,
Zhang, Zhongping
Liu, Iiaojiao
Zhang, Yuting
Zhang, Jiyao
and
Tian, Mingru
2021.
Big Data.
Vol. 1320,
Issue. ,
p.
112.
Klahn, Mathias
Madsen, Per A.
and
Fuhrman, David R.
2021.
A new σ‐transform based Fourier‐Legendre‐Galerkin model for nonlinear water waves.
International Journal for Numerical Methods in Fluids,
Vol. 93,
Issue. 1,
p.
220.
Gao, Zhe
Sun, Z. C.
and
Liang, S. X.
2021.
On two approaches to the third-order solution of surface gravity waves.
Physics of Fluids,
Vol. 33,
Issue. 9,
Tong, Chao
Shao, Yanlin
Bingham, Harry B.
and
Hanssen, Finn‐Christian W.
2021.
An adaptive harmonic polynomial cell method with immersed boundaries: Accuracy, stability, and applications.
International Journal for Numerical Methods in Engineering,
Vol. 122,
Issue. 12,
p.
2945.
Wang, Weizhi
Pákozdi, Csaba
Kamath, Arun
Fouques, Sébastien
and
Bihs, Hans
2022.
A flexible fully nonlinear potential flow model for wave propagation over the complex topography of the Norwegian coast.
Applied Ocean Research,
Vol. 122,
Issue. ,
p.
103103.
Curtin, Conor
and
Ivanov, Rossen
2023.
The Lagrangian Formulation for Wave Motion with a Shear Current and Surface Tension.
Journal of Mathematical Fluid Mechanics,
Vol. 25,
Issue. 4,
Clamond, Didier
Labarbe, Joris
and
Henry, David
2023.
Recovery of steady rotational wave profiles from pressure measurements at the bed.
Journal of Fluid Mechanics,
Vol. 961,
Issue. ,
Ghahraman, Arash
and
Bene, Gyula
2023.
Comprehensive Perturbation Approach to Nonlinear Viscous Gravity–Capillary Surface Waves at Arbitrary Wavelengths in Finite Depth.
Fluids,
Vol. 8,
Issue. 8,
p.
218.
Pakozdi, Csaba
Kamath, Arun
Wang, Weizhi
Martin, Tobias
and
Bihs, Hans
2023.
Efficient Calculation of Hydrodynamic Loads on Offshore Wind Substructures Including Slamming Forces.
Journal of Offshore Mechanics and Arctic Engineering,
Vol. 145,
Issue. 2,
Chen, Yang-Yih
and
Chang, Hsien-Kuo
2024.
Accuracy Examination of the Fourier Series Approximation for Almost Limiting Gravity Waves on Deep Water.
Mathematical and Computational Applications,
Vol. 29,
Issue. 1,
p.
5.
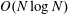 $O(N\log N)$,
$O(N\log N)$, 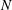 $N$ being the number of Fourier modes. This feature allows the arbitrary precision computation of waves in arbitrary depth, i.e. it works efficiently for Stokes, cnoidal and solitary waves, even for quite large steepnesses, up to approximately 99 % of the maximum steepness for all wavelengths. In particular, the possibility to compute very long (cnoidal) waves accurately is a feature not shared by other algorithms and asymptotic expansions. The method is based on conformal mapping, the Babenko equation rewritten in a suitable way, the pseudo-spectral method and Petviashvili iterations. The efficiency of the algorithm is illustrated via some relevant numerical examples. The code is open source, so interested readers can easily check the claims, use and modify the algorithm.
$N$ being the number of Fourier modes. This feature allows the arbitrary precision computation of waves in arbitrary depth, i.e. it works efficiently for Stokes, cnoidal and solitary waves, even for quite large steepnesses, up to approximately 99 % of the maximum steepness for all wavelengths. In particular, the possibility to compute very long (cnoidal) waves accurately is a feature not shared by other algorithms and asymptotic expansions. The method is based on conformal mapping, the Babenko equation rewritten in a suitable way, the pseudo-spectral method and Petviashvili iterations. The efficiency of the algorithm is illustrated via some relevant numerical examples. The code is open source, so interested readers can easily check the claims, use and modify the algorithm.

