Article contents
Weakly sheared turbulent flows generated by multiscale inhomogeneous grids
Published online by Cambridge University Press: 13 June 2018
Abstract
A group of three multiscale inhomogeneous grids have been tested to generate different types of turbulent shear flows with different mean shear rate and turbulence intensity profiles. Cross hot-wire measurements were taken in a wind tunnel with Reynolds number 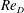 $Re_{D}$ of 6000–20 000, based on the width of the vertical bars of the grid and the incoming flow velocity. The effect of local drag coefficient
$Re_{D}$ of 6000–20 000, based on the width of the vertical bars of the grid and the incoming flow velocity. The effect of local drag coefficient 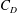 $C_{D}$ on the mean velocity profile is discussed first, and then by modifying the vertical bars to obtain a uniform aspect ratio the mean velocity profile is shown to be predictable using the local blockage ratio profile. It is also shown that, at a streamwise location
$C_{D}$ on the mean velocity profile is discussed first, and then by modifying the vertical bars to obtain a uniform aspect ratio the mean velocity profile is shown to be predictable using the local blockage ratio profile. It is also shown that, at a streamwise location 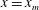 $x=x_{m}$, the turbulence intensity profile along the vertical direction
$x=x_{m}$, the turbulence intensity profile along the vertical direction 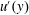 $u^{\prime }(y)$ scales with the wake interaction length
$u^{\prime }(y)$ scales with the wake interaction length 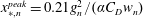 $x_{\ast ,n}^{peak}=0.21g_{n}^{2}/(\unicode[STIX]{x1D6FC}C_{D}w_{n})$ (
$x_{\ast ,n}^{peak}=0.21g_{n}^{2}/(\unicode[STIX]{x1D6FC}C_{D}w_{n})$ ( $\unicode[STIX]{x1D6FC}$ is a constant characterizing the incoming flow condition, and
$\unicode[STIX]{x1D6FC}$ is a constant characterizing the incoming flow condition, and 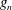 $g_{n}$,
$g_{n}$, 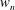 $w_{n}$ are the gap and width of the vertical bars, respectively, at layer
$w_{n}$ are the gap and width of the vertical bars, respectively, at layer  $n$) such that
$n$) such that 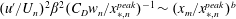 $(u^{\prime }/U_{n})^{2}\unicode[STIX]{x1D6FD}^{2}(C_{D}w_{n}/x_{\ast ,n}^{peak})^{-1}\sim (x_{m}/x_{\ast ,n}^{peak})^{b}$, where
$(u^{\prime }/U_{n})^{2}\unicode[STIX]{x1D6FD}^{2}(C_{D}w_{n}/x_{\ast ,n}^{peak})^{-1}\sim (x_{m}/x_{\ast ,n}^{peak})^{b}$, where  $\unicode[STIX]{x1D6FD}$ is a constant determined by the free-stream turbulence level,
$\unicode[STIX]{x1D6FD}$ is a constant determined by the free-stream turbulence level, 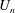 $U_{n}$ is the local mean velocity and
$U_{n}$ is the local mean velocity and 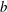 $b$ is a dimensionless power law constant. A general framework of grid design method based on these scalings is proposed and discussed. From the evolution of the shear stress coefficient
$b$ is a dimensionless power law constant. A general framework of grid design method based on these scalings is proposed and discussed. From the evolution of the shear stress coefficient 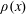 $\unicode[STIX]{x1D70C}(x)$, integral length scale
$\unicode[STIX]{x1D70C}(x)$, integral length scale 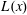 $L(x)$ and the dissipation coefficient
$L(x)$ and the dissipation coefficient 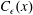 $C_{\unicode[STIX]{x1D716}}(x)$, a simple turbulent kinetic energy model is proposed that describes the evolution of our grid generated turbulence field using one centreline measurement and one vertical profile of
$C_{\unicode[STIX]{x1D716}}(x)$, a simple turbulent kinetic energy model is proposed that describes the evolution of our grid generated turbulence field using one centreline measurement and one vertical profile of 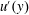 $u^{\prime }(y)$ at the beginning of the evolution. The results calculated from our model agree well with our measurements in the streamwise extent up to
$u^{\prime }(y)$ at the beginning of the evolution. The results calculated from our model agree well with our measurements in the streamwise extent up to 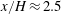 $x/H\approx 2.5$, where
$x/H\approx 2.5$, where 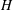 $H$ is the height of the grid, suggesting that it might be possible to design some shear flows with desired mean velocity and turbulence intensity profiles by designing the geometry of a passive grid.
$H$ is the height of the grid, suggesting that it might be possible to design some shear flows with desired mean velocity and turbulence intensity profiles by designing the geometry of a passive grid.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 2
- Cited by



