Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ciriello, Valentina
and
Di Federico, Vittorio
2013.
Analysis of a benchmark solution for non-Newtonian radial displacement in porous media.
International Journal of Non-Linear Mechanics,
Vol. 52,
Issue. ,
p.
46.
Alba, K.
Taghavi, S. M.
and
Frigaard, I. A.
2013.
A weighted residual method for two-layer non-Newtonian channel flows: steady-state results and their stability.
Journal of Fluid Mechanics,
Vol. 731,
Issue. ,
p.
509.
Noble, Pascal
and
Vila, Jean-Paul
2013.
Thin power-law film flow down an inclined plane: consistent shallow-water models and stability under large-scale perturbations.
Journal of Fluid Mechanics,
Vol. 735,
Issue. ,
p.
29.
Pradas, M.
Tseluiko, D.
Ruyer-Quil, C.
and
Kalliadasis, S.
2014.
Pulse dynamics in a power-law falling film.
Journal of Fluid Mechanics,
Vol. 747,
Issue. ,
p.
460.
Miao, Ling
Wu, Wei‐Tao
Aubry, Nadine
and
Massoudi, Mehrdad
2014.
Falling film flow of a viscoelastic fluid along a wall.
Mathematical Methods in the Applied Sciences,
Vol. 37,
Issue. 18,
p.
2840.
Di Cristo, Cristiana
Iervolino, Michele
and
Vacca, Andrea
2014.
Simplified wave models applicability to shallow mud flows modeled as power-law fluids.
Journal of Mountain Science,
Vol. 11,
Issue. 6,
p.
1454.
Olsthoorn, Jason
Stastna, Marek
and
Steinmoeller, Derek
2014.
On the dynamics of vortex-wall interaction in low viscosity shear thinning fluids.
Physics of Fluids,
Vol. 26,
Issue. 1,
Ruyer-Quil, Christian
Kofman, Nicolas
Chasseur, Didier
and
Mergui, Sophie
2014.
Dynamics of falling liquid films.
The European Physical Journal E,
Vol. 37,
Issue. 4,
Martin, M.
Defraeye, T.
Derome, D.
and
Carmeliet, J.
2015.
A film flow model for analysing gravity-driven, thin wavy fluid films.
International Journal of Multiphase Flow,
Vol. 73,
Issue. ,
p.
207.
Allouche, M. H.
Millet, S.
Botton, V.
Henry, D.
Ben Hadid, H.
and
Rousset, F.
2015.
Stability of a flow down an incline with respect to two-dimensional and three-dimensional disturbances for Newtonian and non-Newtonian fluids.
Physical Review E,
Vol. 92,
Issue. 6,
Yadav, Anjalaiah
Chakraborty, S.
and
Usha, R.
2015.
Steady solution of an inverse problem in gravity-driven shear-thinning film flow: Reconstruction of an uneven bottom substrate.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 219,
Issue. ,
p.
65.
Haldar, Samadyuti
2016.
RETRACTED ARTICLE: Effect of electromagnetic field on the stability of viscoelastic fluid film flowing down an inclined plane.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 67,
Issue. 2,
Allouche, M. H.
Botton, V.
Millet, S.
Henry, D.
Dagois-Bohy, S.
Güzel, B.
and
Ben Hadid, H.
2017.
Primary instability of a shear-thinning film flow down an incline: experimental study.
Journal of Fluid Mechanics,
Vol. 821,
Issue. ,
Liu, L.
Yang, L.
Fu, Q.
and
Cui, X.
2018.
Improved modeling of free power-law liquid sheets by weighted-residual approximations.
International Journal of Multiphase Flow,
Vol. 107,
Issue. ,
p.
146.
Pascal, J. P.
D’Alessio, S. J. D.
and
Hasan, M.
2018.
Instability of gravity-driven flow of a heated power-law fluid with temperature dependent consistency.
AIP Advances,
Vol. 8,
Issue. 10,
Pettas, D.
Karapetsas, G.
Dimakopoulos, Y.
and
Tsamopoulos, J.
2019.
Viscoelastic film flows over an inclined substrate with sinusoidal topography. II. Linear stability analysis.
Physical Review Fluids,
Vol. 4,
Issue. 8,
Nsom, Blaise
Ramifidisoa, Lucius
Latrache, Noureddine
and
Ghaemizadeh, Farzaneh
2019.
Linear stability of shear-thinning fluid down an inclined plane.
Journal of Molecular Liquids,
Vol. 277,
Issue. ,
p.
1036.
Mogilevskiy, E.
and
Vakhitova, R.
2019.
Falling film of power-law fluid on a high-frequency oscillating inclined plane.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 269,
Issue. ,
p.
28.
Chakraborty, Symphony
Sheu, Tony Wen-Hann
and
Ghosh, Sukhendu
2019.
Dynamics and stability of a power-law film flowing down a slippery slope.
Physics of Fluids,
Vol. 31,
Issue. 1,
Liu, Lujia
and
Yang, Lijun
2019.
Nonlinear wave evolution of shear-thinning Carreau liquid sheets.
Journal of Fluid Mechanics,
Vol. 859,
Issue. ,
p.
659.
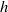 , a local velocity amplitude or the flow rate
, a local velocity amplitude or the flow rate 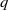 . The models account for the streamwise diffusion of momentum. Comparisons with Orr–Sommerfeld stability analysis and with direct numerical simulation (DNS) show convincing agreement in both linear and nonlinear regimes. The influence of shear-thinning or shear-thickening on the primary instability is shown to be non-trivial. A destabilization of the base flow close to threshold is promoted by the shear-thinning effect, whereas, further from threshold, it tends to stabilize the base flow when the viscous damping of short waves becomes dominant. A reverse situation is observed in the case of shear-thickening fluids. Shear-thinning accelerates solitary waves and promotes a subcritical onset of travelling waves at larger wavenumber than the linear cut-off wavenumber. A conditional stability of the base flow is thus observed. This phenomenon results from a reduction of the effective viscosity at the free surface. When compared with DNS, simulations of the temporal response of the film based on weighted residual models satisfactorily capture the conditional stability of the film.
. The models account for the streamwise diffusion of momentum. Comparisons with Orr–Sommerfeld stability analysis and with direct numerical simulation (DNS) show convincing agreement in both linear and nonlinear regimes. The influence of shear-thinning or shear-thickening on the primary instability is shown to be non-trivial. A destabilization of the base flow close to threshold is promoted by the shear-thinning effect, whereas, further from threshold, it tends to stabilize the base flow when the viscous damping of short waves becomes dominant. A reverse situation is observed in the case of shear-thickening fluids. Shear-thinning accelerates solitary waves and promotes a subcritical onset of travelling waves at larger wavenumber than the linear cut-off wavenumber. A conditional stability of the base flow is thus observed. This phenomenon results from a reduction of the effective viscosity at the free surface. When compared with DNS, simulations of the temporal response of the film based on weighted residual models satisfactorily capture the conditional stability of the film.