Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T13:16:49.224Z Has data issue: false hasContentIssue false
  • English
  • Français

Wall-attached structures of streamwise velocity fluctuations in an adverse-pressure-gradient turbulent boundary layer

Published online by Cambridge University Press:  18 December 2019

Min Yoon ,
Jinyul Hwang Open the ORCID record for Jinyul Hwang [Opens in a new window] ,
Jongmin Yang  and
Hyung Jin Sung Open the ORCID record for Hyung Jin Sung [Opens in a new window]
Min Yoon
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon34141, Korea
Jinyul Hwang
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon34141, Korea School of Mechanical Engineering, Pusan National University, 2 Busandaehak-ro 63beon-gil, Geumjeong-gu, Busan46241, Korea
Jongmin Yang
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon34141, Korea
Hyung Jin Sung*
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon34141, Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

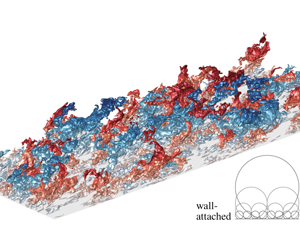
The three-dimensional clusters of streamwise velocity fluctuations ($u$) in turbulent boundary layers (TBLs) are explored from the perspective of the attached-eddy model, which provides a basis for understanding the asymptotic behaviours of high-Reynolds-number wall turbulence in terms of coherent structures. We extract the $u$ clusters from the direct numerical simulation data of a TBL subjected to an adverse pressure gradient ($\unicode[STIX]{x1D6FD}=1.43$). For comparison, the direct numerical simulation data of a zero-pressure-gradient TBL are included. The identified structures are decomposed into attached self-similar, attached non-self-similar, detached self-similar and detached non-self-similar motions with respect to the minimum distance from the wall ($y_{min}$) and height ($l_{y}$). The attached structures ($y_{min}\approx 0$) are the main energy-containing motions and carry approximately half of the streamwise Reynolds stress and the Reynolds shear stress in the logarithmic and outer regions. The sizes of the attached self-similar structures scale with $l_{y}$, and their population density has an inverse-scale distribution over the range $0.4\unicode[STIX]{x1D6FF}<l_{y}<0.58\unicode[STIX]{x1D6FF}$ ($\unicode[STIX]{x1D6FF}$ is the 99 % boundary layer thickness). They also contribute to the logarithmic variation of the streamwise Reynolds stress and to the presence of the $k_{z}^{-1}$ region in the pre-multiplied energy spectra ($k_{z}$ is the spanwise wavenumber), i.e. these structures are universal wall motions in the logarithmic region. The tall attached structures with $l_{y}=O(\unicode[STIX]{x1D6FF})$ are non-self-similar and responsible for the enhancement of the outer large scales under the adverse pressure gradient. They extend beyond $6\unicode[STIX]{x1D6FF}$ in the streamwise direction and penetrate deeply into the near-wall region, which is reminiscent of very-large-scale motions or superstructures. The detached self-similar structures ($y_{min}>0$ and $l_{y}>100\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$) are geometrically isotropic and mainly arise in the outer region, whereas the sizes of the detached non-self-similar structures ($y_{min}>0$ and $l_{y}<100\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$) scale with the Kolmogorov length scale. Here, $\unicode[STIX]{x1D708}$ is the kinematic viscosity and $u_{\unicode[STIX]{x1D70F}}$ the friction velocity. The present study provides a new perspective on the analysis of turbulence structures in the view of the attached-eddy model.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 885 , 25 February 2020 , A12
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Kawamura, H. & Choi, H. 2004 Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to Re 𝜏 = 640. J. Fluids Engng 126 (5), 835–843.CrossRefGoogle Scholar
Agostini, L. & Leschziner, M. A. 2014 On the influence of outer large-scale structures on near-wall turbulence in channel flow. Phys. Fluids 26 (7), 075107.Google Scholar
Ahn, J., Lee, J. H., Lee, J., Kang, J. H. & Sung, H. J. 2015 Direct numerical simulation of a 30R long turbulent pipe flow at Re 𝜏 = 3008. Phys. Fluids 27 (6), 065110.CrossRefGoogle Scholar
Del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.CrossRefGoogle Scholar
Baars, W. J. & Marusic, I. 2020a Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 1. Energy spectra. J. Fluid Mech. 882, A25.CrossRefGoogle Scholar
Baars, W. J. & Marusic, I. 2020b Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 2. Integrated energy and A1. J. Fluid Mech. 882, A26.CrossRefGoogle Scholar
Baidya, R., Philip, J., Hutchins, N., Monty, J. P. & Marusic, I. 2017 Distance-from-the-wall scaling of turbulent motions in wall-bounded flows. Phys. Fluids 29 (2), 020712.CrossRefGoogle Scholar
Bernardini, M. & Pirozzoli, S. 2011 Inner/outer layer interactions in turbulent boundary layers: a refined measure for the large-scale amplitude modulation mechanism. Phys. Fluids 23 (6), 061701.CrossRefGoogle Scholar
Bolotnov, I. A., Lahey, R. T. Jr, Drew, D. A., Jansen, K. E. & Oberai, A. A. 2010 Spectral analysis of turbulence based on the DNS of a channel flow. Comput. Fluids 39 (4), 640–655.CrossRefGoogle Scholar
Borrell, G. & Jiménez, J. 2016 Properties of the turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 801, 554–596.CrossRefGoogle Scholar
Chandran, D., Baidya, R., Monty, J. P. & Marusic, I. 2017 Two-dimensional energy spectra in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 826, R1.CrossRefGoogle Scholar
Chauhan, K., Philip, J., De Silva, C. M., Hutchins, N. & Marusic, I. 2014 The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.CrossRefGoogle Scholar
Clauser, F. H. 1954 Turbulent boundary layers in adverse pressure gradients. J. Aeronaut. Sci. 21 (2), 91–108.CrossRefGoogle Scholar
Coles, D. 1956 The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1 (2), 191–226.CrossRefGoogle Scholar
Dong, S., Lozano-Durán, A., Sekimoto, A. & Jiménez, J. 2017 Coherent structures in statistically stationary homogeneous shear turbulence. J. Fluid Mech. 816, 167–208.CrossRefGoogle Scholar
Han, J., Hwang, J., Yoon, M., Ahn, J. & Sung, H. J. 2019 Azimuthal organization of large-scale motions in a turbulent minimal pipe flow. Phys. Fluids 31 (5), 055113.Google Scholar
Harun, Z., Monty, J. P., Mathis, R. & Marusic, I. 2013 Pressure gradient effects on the large-scale structure of turbulent boundary layers. J. Fluid Mech. 715, 477–498.CrossRefGoogle Scholar
Hellström, L. H., Marusic, I. & Smits, A. J. 2016 Self-similarity of the large-scale motions in turbulent pipe flow. J. Fluid Mech. 792, R1.CrossRefGoogle Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18 (1), 011702.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108 (9), 094501.CrossRefGoogle ScholarPubMed
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-layer Meteorol. 145 (2), 273–306.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.CrossRefGoogle Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.CrossRefGoogle Scholar
Hwang, J., Lee, J. & Sung, H. J. 2016a Influence of large-scale accelerating motions on turbulent pipe and channel flows. J. Fluid Mech. 804, 420–441.CrossRefGoogle Scholar
Hwang, J., Lee, J., Sung, H. J. & Zaki, T. A. 2016b Inner–outer interactions of large-scale structures in turbulent channel flow. J. Fluid Mech. 790, 128–157.CrossRefGoogle Scholar
Hwang, J. & Sung, H. J. 2017 Influence of large-scale motions on the frictional drag in a turbulent boundary layer. J. Fluid Mech. 829, 751–779.CrossRefGoogle Scholar
Hwang, J. & Sung, H. J. 2018 Wall-attached structures of velocity fluctuations in a turbulent boundary layer. J. Fluid Mech. 856, 958–983.CrossRefGoogle Scholar
Hwang, J. & Sung, H. J. 2019 Wall-attached clusters for the logarithmic velocity law in turbulent pipe flow. Phys. Fluids 31 (5), 055109.Google Scholar
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.CrossRefGoogle Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.CrossRefGoogle Scholar
Hwang, Y. 2016 Mesolayer of attached eddies in turbulent channel flow. Phys. Rev. Fluids 1 (6), 064401.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010 Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105 (4), 044505.CrossRefGoogle ScholarPubMed
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.CrossRefGoogle Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.CrossRefGoogle Scholar
Kim, K., Baek, S. J. & Sung, H. J. 2002 An implicit velocity decoupling procedure for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 38 (2), 125–138.CrossRefGoogle Scholar
Kim, S., Huang, W. X. & Sung, H. J. 2010 Constructive and destructive interaction modes between two tandem flexible flags in viscous flow. J. Fluid Mech. 661, 511–521.CrossRefGoogle Scholar
Kitsios, V., Atkinson, C., Sillero, J. A., Borrell, G., Gungor, A. G., Jiménez, J. & Soria, J. 2016 Direct numerical simulation of a self-similar adverse pressure gradient turbulent boundary layer. Intl J. Heat Fluid Flow 61, 129–136.CrossRefGoogle Scholar
Kitsios, V., Sekimoto, A., Atkinson, C., Sillero, J. A., Borrell, G., Gungor, A. G., Jiménez, J. & Soria, J. 2017 Direct numerical simulation of a self-similar adverse pressure gradient turbulent boundary layer at the verge of separation. J. Fluid Mech. 829, 392–419.CrossRefGoogle Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (4), 741–773.CrossRefGoogle Scholar
Kwon, Y. S., Hutchins, N. & Monty, J. P. 2016 On the use of the Reynolds decomposition in the intermittent region of turbulent boundary layers. J. Fluid Mech. 794, 5–16.CrossRefGoogle Scholar
Lee, J., Lee, J. H., Lee, J. H. & Sung, H. J. 2010 Coherent structures in turbulent boundary layers with adverse pressure gradients. J. Turbul. 11 (28), 1–20.Google Scholar
Lee, J. H. 2017 Large-scale motions in turbulent boundary layers subjected to adverse pressure gradients. J. Fluid Mech. 810, 323–361.CrossRefGoogle Scholar
Lee, J. H. & Sung, H. J. 2008 Effects of an adverse pressure gradient on a turbulent boundary layer. Intl J. Heat Fluid Flow 29 (3), 568–578.CrossRefGoogle Scholar
Lee, J. H. & Sung, H. J. 2009 Structures in turbulent boundary layers subjected to adverse pressure gradients. J. Fluid Mech. 639, 101–131.CrossRefGoogle Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Lee, M. & Moser, R. D. 2019 Spectral analysis of the budget equation in turbulent channel flows at high Reynolds number. J. Fluid Mech. 860, 886–938.CrossRefGoogle Scholar
Lozano-Durán, A., Flores, O. & Jiménez, J. 2012 The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 694, 100–130.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.CrossRefGoogle Scholar
Maciel, Y., Gungor, A. G. & Simens, M. 2017a Structural differences between small and large momentum-defect turbulent boundary layers. Intl J. Heat Fluid Flow 67, 95–110.CrossRefGoogle Scholar
Maciel, Y., Simens, M. P. & Gungor, A. G. 2017b Coherent structures in a non-equilibrium large-velocity-defect turbulent boundary layer. Flow Turbul. Combust. 98 (1), 1–20.CrossRefGoogle Scholar
Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13 (3), 735–743.CrossRefGoogle Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15 (8), 2461–2464.CrossRefGoogle Scholar
Marusic, I. & Monty, J. P. 2019 Attached eddy model of wall turbulence. Annu. Rev. Fluid Mech. 51, 49–74.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
Marusic, I. & Perry, A. E. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.CrossRefGoogle Scholar
Marusic, I., Uddin, A. K. M. & Perry, A. E. 1997 Similarity law for the streamwise turbulence intensity in zero-pressure-gradient turbulent boundary layers. Phys. Fluids 9 (12), 3718–3726.CrossRefGoogle Scholar
Mellor, G. L. & Gibson, D. M. 1966 Equilibrium turbulent boundary layers. J. Fluid Mech. 24 (2), 225–253.CrossRefGoogle Scholar
Moisy, F. & Jiménez, J. 2004 Geometry and clustering of intense structures in isotropic turbulence. J. Fluid Mech. 513, 111–133.CrossRefGoogle Scholar
Nickels, T. B. & Marusic, I. 2001 On the different contributions of coherent structures to the spectra of a turbulent round jet and a turbulent boundary layer. J. Fluid Mech. 448, 367–385.CrossRefGoogle Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the k 1-1 law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95 (7), 074501.CrossRefGoogle Scholar
Nickels, T. B., Marusic, I., Hafez, S., Hutchins, N. & Chong, M. S. 2007 Some predictions of the attached eddy model for a high Reynolds number boundary layer. Phil. Trans. R. Soc. Lond. A 365 (1852), 807–822.CrossRefGoogle ScholarPubMed
Örlü, R., Fiorini, T., Segalini, A., Bellani, G., Talamelli, A. & Alfredsson, P. H. 2017 Reynolds stress scaling in pipe flow turbulence – first results from CICLoPE. Phil. Trans. R. Soc. Lond. A 375 (2089), 20160187.CrossRefGoogle ScholarPubMed
Osawa, K. & Jiménez, J. 2018 Intense structures of different momentum fluxes in turbulent channels. Phys. Rev. Fluids 3 (8), 084603.CrossRefGoogle Scholar
Park, T. S. & Sung, H. J. 1995 A nonlinear low-Reynolds-number 𝜅–𝜀 model for turbulent separated and reattaching flows. I. Flow field computations. Intl J. Heat Mass. Transfer 38 (14), 2657–2666.CrossRefGoogle Scholar
Perry, A. E. & Abell, C. J. 1977 Asymptotic similarity of turbulence structures in smooth- and rough-walled pipes. J. Fluid Mech. 79 (4), 785–799.CrossRefGoogle Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Perry, A. E. & Li, J. D. 1990 Experimental support for the attached-eddy hypothesis in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 218, 405–438.CrossRefGoogle Scholar
Perry, A. E., Li, J. D. & Marusic, I. 1988 Novel methods of modeling wall turbulence. In 26th Aerospace Sciences Meeting, AIAA 88-0219, AIAA.Google Scholar
Perry, A. E., Li, J. D. & Marusic, I. 1991 Towards a closure scheme for turbulent boundary layers using the attached eddy hypothesis. Phil. Trans. R. Soc. Lond. A 336 (1640), 67–79.Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall–wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.CrossRefGoogle Scholar
Perry, A. E., Marusic, I. & Li, J. D. 1994 Wall turbulence closure based on classical similarity laws and the attached eddy hypothesis. Phys. Fluids 6 (2), 1024–1035.CrossRefGoogle Scholar
Perry, A. E., Marusic, I. & Jones, M. B. 2002 On the streamwise evolution of turbulent boundary layers in arbitrary pressure gradients. J. Fluid Mech. 461, 61–91.CrossRefGoogle Scholar
Pirozzoli, S. & Bernardini, M. 2013 Probing high-Reynolds-number effects in numerical boundary layers. Phys. Fluids 25 (2), 021704.CrossRefGoogle Scholar
Samie, M., Marusic, I., Hutchins, N., Fu, M. K., Fan, Y., Hultmark, M. & Smits, A. J. 2018 Fully resolved measurements of turbulent boundary layer flows up to Re 𝜏 = 20 000. J. Fluid Mech. 851, 391–415.CrossRefGoogle Scholar
Sillero, J.2014. High Reynolds number turbulent boundary layers. PhD thesis, Universidad Politénica de Madrid.Google Scholar
Skåre, P. E. & Krogstad, P. Å. 1994 A turbulent equilibrium boundary layer near separation. J. Fluid Mech. 272, 319–348.CrossRefGoogle Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High–Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
Townsend, A. A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11 (1), 97–120.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vallikivi, M., Hultmark, M. & Smits, A. J. 2015 Turbulent boundary layer statistics at very high Reynolds number. J. Fluid Mech. 779, 371–389.CrossRefGoogle Scholar
Wei, T., Fife, P., Klewicki, J. & Mcmurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.CrossRefGoogle Scholar
Yang, J., Hwang, J. & Sung, H. J. 2019 Influence of wall-attached structures on the boundary of quiescent core region in turbulent pipe flow. Phys. Rev. Fluids 4 (11), 114606.CrossRefGoogle Scholar
Yoon, M., Hwang, J., Lee, J., Sung, H. J. & Kim, J. 2016 Large-scale motions in a turbulent channel flow with the slip boundary condition. Intl J. Heat Fluid Flow 61, 96–107.CrossRefGoogle Scholar
Yoon, M., Hwang, J. & Sung, H. J. 2018 Contribution of large-scale motions to the skin friction in a moderate adverse pressure gradient turbulent boundary layer. J. Fluid Mech. 848, 288–311.CrossRefGoogle Scholar