Article contents
Wake behind a discontinuous cylinder: unveiling the role of the large scales in wake growth and entrainment
Published online by Cambridge University Press: 07 February 2022
Abstract
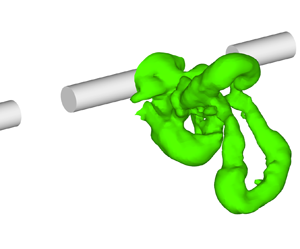
The turbulent flow in the wake of a discontinuous cylinder (DC) was investigated. The DC geometry consisted of cylinder segments  $5D$ long (with
$5D$ long (with  $D$ being the diameter of the cylinder) separated by gaps of width
$D$ being the diameter of the cylinder) separated by gaps of width  $2.5D$. Particle image velocimetry and hot-wire anemometry were used to analyse the flow at two Reynolds numbers,
$2.5D$. Particle image velocimetry and hot-wire anemometry were used to analyse the flow at two Reynolds numbers,  $Re = 4000$ and
$Re = 4000$ and  $10\,000$, for
$10\,000$, for  $x/D \le 180$. Large eddy simulations for both the DC and the infinite continuous cylinder (CC) wakes were also carried out at
$x/D \le 180$. Large eddy simulations for both the DC and the infinite continuous cylinder (CC) wakes were also carried out at  $Re = 10\,000$. The DC configuration was devised to trigger the shedding of horseshoe vortices (HSV) in the very-near-wake region with the intent of illustrating the role that these three-dimensional HSVs, previously identified in the far-wake region of CC, play in the entrainment process in turbulent wakes. The DC geometry produced HSVs by the interaction between the high momentum flow through the gaps and the main spanwise vortex shed behind each cylinder segment, while in the CC wake they evolve from near-wake instabilities straddled with hairpin vortices that detach spanwise vorticity from the shed Kármán vortices. The DC wake was found to grow and spread in the transverse direction with a much faster rate than for the CC wake, up until approximately
$Re = 10\,000$. The DC configuration was devised to trigger the shedding of horseshoe vortices (HSV) in the very-near-wake region with the intent of illustrating the role that these three-dimensional HSVs, previously identified in the far-wake region of CC, play in the entrainment process in turbulent wakes. The DC geometry produced HSVs by the interaction between the high momentum flow through the gaps and the main spanwise vortex shed behind each cylinder segment, while in the CC wake they evolve from near-wake instabilities straddled with hairpin vortices that detach spanwise vorticity from the shed Kármán vortices. The DC wake was found to grow and spread in the transverse direction with a much faster rate than for the CC wake, up until approximately  $x/D \approx 50$. Prior to this location, the enhanced growth rate caused by the shear-aligned HSV led to a wake width of approximately 3 times that of the CC wake, with a maximum mean velocity deficit that was approximately half.
$x/D \approx 50$. Prior to this location, the enhanced growth rate caused by the shear-aligned HSV led to a wake width of approximately 3 times that of the CC wake, with a maximum mean velocity deficit that was approximately half.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 1
- Cited by



