Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T18:41:51.741Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex shedding and heat transfer in rotationally oscillating cylinders

Published online by Cambridge University Press:  01 May 2014

Prabu Sellappan Open the ORCID record for Prabu Sellappan [Opens in a new window]  and
Tait Pottebaum
Prabu Sellappan*
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089, USA
Tait Pottebaum
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

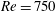Wake formation and heat transfer from a rotationally oscillating circular cylinder in cross-flow at $\mathit{Re}= 750$ are studied. Two aspects, the effect of cylinder forcing on vortex shedding and the effect of the wake structures on convective heat transfer, are studied. Cylinder forcing conditions range between 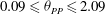$0.09 \leq \theta _{PP} \leq 2.09$, where 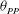$\theta _{PP}$ is the peak-to-peak oscillation amplitude in radians and 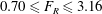$0.70 \leq F_{R} \leq 3.16$, where 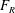$F_{R}$ is the ratio of forcing frequency to natural shedding frequency. Digital particle image velocimetry (DPIV) is used to obtain quantitative wake structure information. Wake modes, and regions of the parameter space in which they occur, are identified for both heated and unheated cylinders. For the heated cylinder, cylinder forcing is found to affect the convective heat-transfer rate. Certain wake modes, including newly discovered wake modes synchronized over multiple oscillation cycles, are found to correlate with significant heat-transfer enhancement. Cylinder tangential velocity is also found to affect the heat-transfer rate in certain regions of the parameter space.

JFM classification

Convection: Convection Vortex Flows: Vortex shedding Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 748 , 10 June 2014 , pp. 549 - 579
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baek, S. J. & Sung, H. J. 2000 Quasi-periodicity in the wake of a rotationally oscillating cylinder. J. Fluid Mech. 408, 275–300.CrossRefGoogle Scholar
Bearman, P. W. 1969 On vortex shedding from a circular cylinder in critical Reynolds number regime. J. Fluid Mech. 37 (3), 577–585.CrossRefGoogle Scholar
Bouhairie, S. & Chu, V. H. 2007 Two-dimensional simulation of unsteady heat transfer from a circular cylinder in crossflow. J. Fluid Mech. 570, 177–215.CrossRefGoogle Scholar
Chang, B. H. & Mills, A. F. 2004 Effect of aspect ratio on forced convection heat transfer from cylinders. Intl J. Heat Mass Transfer 47 (6–7), 1289–1296.CrossRefGoogle Scholar
Dennis, S. C. R., Nguyen, P. & Kocabiyik, S. 2000 The flow induced by a rotationally oscillating and translating circular cylinder. J. Fluid Mech. 407, 123–144.CrossRefGoogle Scholar
Du, L. & Dalton, C. 2013 LES calculation for uniform flow past a rotationally oscillating cylinder. J. Fluids Struct. 42, 40–54.CrossRefGoogle Scholar
Eisenlohr, H. & Eckelmann, H. 1989 Vortex splitting and its consequences in the vortex street wake of cylinders at low Reynolds number. Phys. Fluids A 1 (2), 189–192.CrossRefGoogle Scholar
Fujisawa, N., Kawaji, Y. & Ikemoto, K. 2001 Feedback control of vortex shedding from a circular cylinder by rotational oscillations. J. Fluids Struct. 15 (1), 23–37.CrossRefGoogle Scholar
Fujisawa, N., Tanahashi, S. & Srinivas, K. 2005 Evaluation of pressure field and fluid forces on a circular cylinder with and without rotational oscillation using velocity data from PIV measurement. Meas. Sci. Technol. 16 (4), 989–996.CrossRefGoogle Scholar
Hammache, M. & Gharib, M. 1989 A novel method to promote parallel vortex shedding in the wake of circular cylinders. Phys. Fluids A 1 (10), 1611–1614.CrossRefGoogle Scholar
He, J. W., Glowinski, R., Metcalfe, R., Nordlander, A. & Periaux, J. 2000 Active control and drag optimization for flow past a circular cylinder I. Oscillatory cylinder rotation. J. Comput. Phys. 163 (1), 83–117.CrossRefGoogle Scholar
Hu, H. & Koochesfahani, M. M. 2011 Thermal effects on the wake of a heated circular cylinder operating in mixed convection regime. J. Fluid Mech. 685, 235–270.CrossRefGoogle Scholar
Incropera, F. P. & Dewitt, D. P. 1996 Fundamentals of Heat and Mass Transfer. 4th edn John Wiley & Sons, New York.Google Scholar
Jian, D., Xue-ming, S. & An-lu, R. 2007 Vanishing of three-dimensionality in the wake behind a rotationally oscillating circular cylinder. J. Hydrodyn. B 19 (6), 751–755.Google Scholar
Kumar, S., Lopez, C., Probst, O., Francisco, G., Askari, D. & Yang, Y. 2013 Flow past a rotationally oscillating cylinder. J. Fluid Mech. 735, 307–346.CrossRefGoogle Scholar
Kwon, K. & Choi, H. 1996 Control of laminar vortex shedding behind a circular cylinder using splitter plates. Phys. Fluids 8 (2), 479–486.CrossRefGoogle Scholar
Lee, S. J. & Lee, J. Y. 2006 Flow structure of wake behind a rotationally oscillating circular cylinder. J. Fluids Struct. 22 (8), 1097–1112.CrossRefGoogle Scholar
Lee, S. J. & Lee, J. Y. 2008 PIV measurements of the wake behind a rotationally oscillating circular cylinder. J. Fluids Struct. 24 (1), 2–17.CrossRefGoogle Scholar
Lo Jacono, D., Leontini, J. S., Thompson, M. C. & Sheridan, J. 2010 Modification of three-dimensional transition in the wake of a rotationally oscillating cylinder. J. Fluid Mech. 643, 349–362.CrossRefGoogle Scholar
Lu, L., Qin, J.-M., Teng, B. & Li, Y.-C. 2011 Numerical investigations of lift suppression by feedback rotary oscillation of circular cylinder at low Reynolds number. Phys. Fluids 23 (3), 033601.CrossRefGoogle Scholar
Lu, X. Y. & Sato, J. 1996 A numerical study of flow past a rotationally oscillating circular cylinder. J. Fluids Struct. 10 (8), 829–849.CrossRefGoogle Scholar
Mahfouz, F. M. & Badr, H. M. 2000a Flow structure in the wake of a rotationally oscillating cylinder. Trans. ASME J. Fluids Engng 122 (2), 290–301.CrossRefGoogle Scholar
Mahfouz, F. M. & Badr, H. M. 2000b Forced convection from a rotationally oscillating cylinder placed in a uniform stream. Intl J. Heat Mass Transfer 43 (17), 3093–3104.CrossRefGoogle Scholar
Morgan, V. T. 1975 The overall convective heat transfer from smooth circular cylinders. Adv. Heat Transfer 11, 199–264.CrossRefGoogle Scholar
Nazarinia, M., Lo Jacono, D., Thompson, M. C. & Sheridan, J. 2012 Flow over a cylinder subjected to combined translational and rotational oscillations. J. Fluids Struct. 32, 135–145.CrossRefGoogle Scholar
Nishihara, T., Kaneko, S. & Watanabe, T. 2005 Characteristics of fluid dynamic forces acting on a circular cylinder oscillated in the streamwise direction and its wake patterns. J. Fluids Struct. 20 (4), 505–518.CrossRefGoogle Scholar
Norberg, C. 1994 An experimental investigation of the flow around a circular-cylinder—influence of aspect ratio. J. Fluid Mech. 258, 287–316.CrossRefGoogle Scholar
Norberg, C. 2001 Flow around a circular cylinder: aspects of fluctuating lift. J. Fluids Struct. 15, 459–469.CrossRefGoogle Scholar
Poncet, P. 2002 Vanishing of mode B in the wake behind a rotationally oscillating circular cylinder. Phys. Fluids 14 (6), 2021–2023.CrossRefGoogle Scholar
Posdziech, O. & Grundmann, R. 2007 A systematic approach to the numerical calculation of fundamental quantities of the two-dimensional flow over a circular cylinder. J. Fluids Struct. 23, 479–499.CrossRefGoogle Scholar
Pottebaum, T.2003 The relationship between near-wake structure and heat transfer for an oscillating circular cylinder in cross-flow. PhD thesis, California Institute of Technology, Pasadena, CA, USA.CrossRefGoogle Scholar
Pottebaum, T. S. & Gharib, M. 2006 Using oscillations to enhance heat transfer for a circular cylinder. Intl J. Heat Mass Transfer 49 (17–18), 3190–3210.CrossRefGoogle Scholar
Roshko, A. 1954 On the Drag and Shedding Frequency of Two-Dimensional Bluff Bodies. Tech. Note. vol. 3169, Nat. Adv. Comm. Aero.Google Scholar
Roshko, A. 1955 On the wake and drag of bluff bodies. J. Aero. Sci. 22 (2), 124–132.CrossRefGoogle Scholar
Roshko, A. 1961 Experiments on the flow past a circular cylinder at very high Reynolds number. J. Fluid Mech. 10 (3), 345–356.CrossRefGoogle Scholar
Saad, M., Lee, L. & Lee, T. 2007 Shear layers of a circular cylinder with rotary oscillation. Exp. Fluids 43 (4), 569–578.CrossRefGoogle Scholar
Sellappan, P.2013 Wake modes of rotationally oscillating circular cylinder in cross-flow and its relationship with heat transfer. PhD thesis, University of Southern California, Los Angeles, CA, USA.Google Scholar
Sellappan, P. & Pottebaum, T. 2014 Wake modes of rotationally oscillating cylinders at $\mathit{Re} =150$ . J. Fluids Struct. 46, 29–41.CrossRefGoogle Scholar
Sparrow, E. M., Abraham, J. P. & Tong, J. C. K. 2004 Archival correlations for average heat transfer coefficients for non-circular and circular cylinders and for spheres in cross-flow. Intl J. Heat Mass Transfer 47 (24), 5285–5296.CrossRefGoogle Scholar
Sreenivasan, K. & Ramachandran, A. 1961 Effect of vibration on heat transfer from a horizontal cylinder to a normal air stream. Intl J. Heat Mass Transfer 3 (1), 60–67.CrossRefGoogle Scholar
Szepessy, S. & Bearman, P. W. 1992 Aspect ratio and end plate effects on vortex shedding from a circular cylinder. J. Fluid Mech. 234, 191–217.CrossRefGoogle Scholar
Thiria, B., Goujon-Durand, S. & Wesfreid, J. E. 2006 The wake of a cylinder performing rotary oscillations. J. Fluid Mech. 560, 123–147.CrossRefGoogle Scholar
Thiria, B. & Wesfreid, J. E. 2007 Stability properties of forced wakes. J. Fluid Mech. 579, 137–161.CrossRefGoogle Scholar
Tokumaru, P. T. & Dimotakis, P. E. 1991 Rotary oscillation control of a cylinder wake. J. Fluid Mech. 224, 77–90.CrossRefGoogle Scholar
Vit, T., Ren, M., Travnicek, Z., Marsik, F. & Rindt, C. C. M. 2007 The influence of temperature gradient on the Strouhal–Reynolds number relationship for water and air. Exp. Therm. Fluid Sci. 31 (7), 751–760.CrossRefGoogle Scholar
Williamson, C. H. K. 1988 Defining a universal and continuous Strouhal–Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Phys. Fluids 31 (10), 2742–2744.CrossRefGoogle Scholar
Williamson, C. H. K. 1989 Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds-numbers. J. Fluid Mech. 206, 579–627.CrossRefGoogle Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.CrossRefGoogle Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2 (4), 355–381.CrossRefGoogle Scholar