Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chen, Zhen
You, Changfu
Wang, Haiming
and
Xie, Ning
2020.
A novel technical route based on wet flue gas desulfurization process for flue gas dehumidification, water and heat recovery.
Applied Thermal Engineering,
Vol. 171,
Issue. ,
p.
115102.
Houdroge, F. Y.
Leweke, T.
Hourigan, K.
and
Thompson, M. C.
2020.
Wake dynamics and flow-induced vibration of a freely rolling cylinder.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
Chizfahm, Amir
Joshi, Vaibhav
and
Jaiman, Rajeev
2021.
Transverse flow-induced vibrations of a sphere in the proximity of a free surface: A numerical study.
Journal of Fluids and Structures,
Vol. 101,
Issue. ,
p.
103224.
Niven, Robert K.
2021.
Invariance Properties of the Entropy Production, and the Entropic Pairing of Inertial Frames of Reference by Shear-Flow Systems.
Entropy,
Vol. 23,
Issue. 11,
p.
1515.
Rajamuni, Methma M.
Hourigan, Kerry
and
Thompson, Mark C.
2021.
Vortex-induced vibration of a sphere close to or piercing a free surface.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Kovalev, D.
Eshbal, L.
and
van Hout, R.
2022.
Three-dimensional flow field measurements in the wake of a tethered sphere crossing the onset of vortex induced vibrations.
Journal of Fluid Mechanics,
Vol. 943,
Issue. ,
Draycott, S.
Pillai, A.C.
Gabl, R.
Stansby, P.K.
and
Davey, T.
2022.
An experimental assessment of the effect of current on wave buoy measurements.
Coastal Engineering,
Vol. 174,
Issue. ,
p.
104114.
Yao, Weiguang
Jia, Xiaoyu
Zhang, Hui
and
Gui, Mingyue
2023.
Suppression of vortex-induced vibration of an elastically mounted sphere by electromagnetic force.
Physics of Fluids,
Vol. 35,
Issue. 9,
Fu, Jiahao
He, Guojian
Huang, Lei
Dey, Subhasish
and
Fang, Hongwei
2023.
Swaying motions of submerged flexible vegetation.
Journal of Fluid Mechanics,
Vol. 971,
Issue. ,
Yao, Weiguang
Zhang, Hui
Jiang, Daiwen
Gui, Mingyue
Zhao, Zijie
and
Chen, Zhihua
2023.
The transformation mechanisms of vortex structures on vortex-induced vibration of an elastically mounted sphere by Lorentz force.
Ocean Engineering,
Vol. 280,
Issue. ,
p.
114436.
Wang, Junlei
Zhang, Ye
Hu, Guobiao
and
Zhang, Wenming
2023.
Wake-induced vibration and heat transfer characteristics of three tandem semi-circular cylinders.
Journal of Fluids and Structures,
Vol. 123,
Issue. ,
p.
104004.
Duranay, Aytekin
2024.
Numerical and experimental investigation of vortex formation modes on a freely vibrating circular cylinder at high Reynolds numbers.
Applied Ocean Research,
Vol. 144,
Issue. ,
p.
103909.
Zhang, Zhiyu
Lu, Jianfeng
and
Zhang, Xing
2024.
Global stability analysis of flow-induced-vibration problems using an immersed boundary method.
Journal of Fluids and Structures,
Vol. 130,
Issue. ,
p.
104187.
Jia, Xuyi
Gong, Chunlin
Ji, Wen
and
Li, Chunna
2024.
An accuracy-enhanced transonic flow prediction method fusing deep learning and a reduced-order model.
Physics of Fluids,
Vol. 36,
Issue. 5,
Zhao, Zijie
Hou, Dianfeng
Yang, Bingxian
Jiang, Daiwen
and
Yao, Weiguang
2024.
Transverse vortex-induced vibration of a sphere with the application of Lorentz force at low Reynolds number.
Physics of Fluids,
Vol. 36,
Issue. 10,
Sarkar, Sandip
and
De, Arnab Kumar
2025.
Viscous Magnus force for a transversely rotating sphere undergoing vortex-induced vibration.
Physics of Fluids,
Vol. 37,
Issue. 1,
Bao, Di
Plihon, Nicolas
and
Bourgoin, Mickaël
2025.
Bi-stable cross-flow pendulum at high Reynolds numbers: experimental investigation and stochastic modelling.
Journal of Fluid Mechanics,
Vol. 1007,
Issue. ,
Weng, Shun
Wu, Liying
Zhang, Lanbin
Gao, Ke
Zhang, Junshu
Zhang, Zhiyue
and
Dai, Huliang
2025.
Multi-directional wind energy harvesting based on the coupling effect between a piezoelectric beam and an elastic-supported sphere.
Journal of Zhejiang University-SCIENCE A,
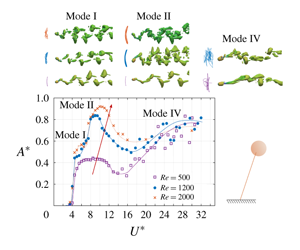
 $U^{\ast }\in [3,32]$. The flow was governed by the incompressible Navier–Stokes equations, while the dynamic motion of the sphere was governed by coupled Newtonian mechanics. A new fluid–structure interaction (FSI) solver was implemented to efficiently solve the coupled FSI system. The effect of Reynolds number was found to be significant in the mode I and II regimes. A progressive increase in the response amplitude was observed as the Reynolds number was increased, especially in the mode II regime. The overall sphere response at the highest Reynolds number was relatively close to the observed behaviour of previous higher-
$U^{\ast }\in [3,32]$. The flow was governed by the incompressible Navier–Stokes equations, while the dynamic motion of the sphere was governed by coupled Newtonian mechanics. A new fluid–structure interaction (FSI) solver was implemented to efficiently solve the coupled FSI system. The effect of Reynolds number was found to be significant in the mode I and II regimes. A progressive increase in the response amplitude was observed as the Reynolds number was increased, especially in the mode II regime. The overall sphere response at the highest Reynolds number was relatively close to the observed behaviour of previous higher- $Re$ experimental studies. An aperiodic mode IV response was observed at higher reduced velocities beyond the mode II range in each case, without the intervening mode III regime. However, as the mass ratio increased from 0.8 to 80, the random response of the sphere (mode IV) gradually became more regular, showing a mode III response (characterized by a near-periodic sphere oscillation) at
$Re$ experimental studies. An aperiodic mode IV response was observed at higher reduced velocities beyond the mode II range in each case, without the intervening mode III regime. However, as the mass ratio increased from 0.8 to 80, the random response of the sphere (mode IV) gradually became more regular, showing a mode III response (characterized by a near-periodic sphere oscillation) at  $U^{\ast }=30$. Thus, if the inertia of the system is low, mode IV appears at lower
$U^{\ast }=30$. Thus, if the inertia of the system is low, mode IV appears at lower  $U^{\ast }$ values, while for high-inertia systems, mode IV appears at high
$U^{\ast }$ values, while for high-inertia systems, mode IV appears at high  $U^{\ast }$ values beyond a mode III response.
$U^{\ast }$ values beyond a mode III response.