Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-01T03:47:36.092Z Has data issue: false hasContentIssue false
  • English
  • Français

Viscous effects on the acoustics and stability of a shear layer over an impedance wall

Published online by Cambridge University Press:  01 December 2016

Doran Khamis  and
Edward James Brambley Open the ORCID record for Edward James Brambley [Opens in a new window]
Doran Khamis
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK
Edward James Brambley*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The effect of viscosity and thermal conduction on the acoustics in a shear layer above an impedance wall is investigated numerically and asymptotically by solving the linearised compressible Navier–Stokes equations (LNSE). It is found that viscothermal effects can be as important as shear, and therefore including shear while neglecting viscothermal effects by solving the linearised Euler equations (LEE) is questionable. In particular, the damping rate of upstream-propagating waves is found to be under-predicted by the LEE, and dramatically so in certain instances. The effects of viscosity on stability are also found to be important. Short wavelength disturbances are stabilised by viscosity, greatly altering the characteristic wavelength and maximum growth rate of instability. For the parameters considered here (chosen to be typical of aeroacoustic situations), the Reynolds number below which the flow stabilises ranges from 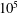$10^{5}$ to 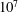$10^{7}$. By assuming a thin but non-zero-thickness boundary layer, asymptotic analysis leads to a system of boundary layer governing equations for the acoustics. This system may be solved numerically to produce an effective impedance boundary condition, applicable at the wall of a uniform inviscid flow, that accounts for both the shear and viscosity within the boundary layer. An alternative asymptotic analysis in the high-frequency limit yields a different set of boundary layer equations, which are solved to yield analytic solutions. The acoustic mode shapes and axial wavenumbers from both asymptotic analyses compare well with numerical solutions of the full LNSE. A closed-form effective impedance boundary condition is derived from the high-frequency asymptotics, suitable for application in frequency domain numerical simulations. Finally, surface waves are considered, and it is shown that a viscous flow over an impedance lining supports a greater number of surface wave modes than an inviscid flow.

JFM classification

Acoustics: Aeroacoustics Boundary Layers: Boundary layer stability Compressible Flows: Compressible Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 810 , 10 January 2017 , pp. 489 - 534
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

A preliminary version of some of this work was presented at the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, 2015, paper 2015-2229.

References

Alomar, A. & Aurégan, Y. 2016 PIV measurement of a porous liner in a duct with flow. In 22nd AIAA/CEAS Aeroacoustics Conference. American Institute of Aeronautics and Astronautics.Google Scholar
Aurégan, Y. & Leroux, M. 2008 Experimental evidence of an instability over an impedance wall in a duct with flow. J. Sound Vib. 317, 432–439.Google Scholar
Aurégan, Y., Starobinski, R. & Pagneux, V. 2001 Influence of grazing flow and dissipation effects on the acoustic boundary conditions at a lined wall. J. Acoust. Soc. Am. 109 (1), 59–64.Google Scholar
Bers, A. 1983 Space-time evolution of plasma instabilities – absolute and convective. In Basic Plasma Physics, Handbook of Plasma Physics (ed. Galeev, A. A. & Sudan, R. N.), vol. 1, pp. 451–517. North–Holland.Google Scholar
Boyer, G., Piot, E. & Brazier, J.-P. 2011 Theoretical investigation of hydrodynamic surface mode in a lined duct with sheared flow and comparison with experiment. J. Sound Vib. 330, 1793–1809.Google Scholar
Brambley, E. J. 2009 Fundamental problems with the model of uniform flow over acoustic linings. J. Sound Vib. 322, 1026–1037.Google Scholar
Brambley, E. J. 2011a Acoustic implications of a thin viscous boundary layer over a compliant surface or permeable liner. J. Fluid Mech. 678, 348–378.Google Scholar
Brambley, E. J. 2011b Well-posed boundary condition for acoustic liners in straight ducts with flow. AIAA J. 49 (6), 1272–1282.Google Scholar
Brambley, E. J. 2013 Surface modes in sheared boundary layers over impedance linings. J. Sound Vib. 332, 3750–3767.Google Scholar
Brambley, E. J.2015 DRP schemes perform badly for decaying or growing oscillations. AIAA Paper 2015-2540.CrossRefGoogle Scholar
Brambley, E. J. 2016 Optimized finite-difference (DRP) schemes perform poorly for decaying or growing oscillations. J. Comput. Phys. 324, 258–274.CrossRefGoogle Scholar
Briggs, R. J. 1964 Electron-Stream Interaction with Plasmas. MIT.Google Scholar
Burak, M., Billson, M., Eriksson, L.-E. & Baralon, S.2008 Validation of a time & frequency domain grazing flow acoustic liner model. AIAA Paper 2008-2929.Google Scholar
Burak, M. O., Billson, M., Eriksson, L.-E. & Baralon, S. 2009 Validation of a time- and frequency-domain grazing flow acoustic liner model. AIAA J. 47 (8), 1841–1848.Google Scholar
Cramer, M. S. 2012 Numerical estimates for the bulk viscosity of ideal gases. Phys. Fluids 24 (6), 066102.Google Scholar
Dai, X. & Aurégan, Y. 2016 Influence of shear flow on liner impedance computed by multimodal method. In 22nd AIAA/CEAS Aeroacoustics Conference. American Institute of Aeronautics and Astronautics.Google Scholar
Doak, P. E. & Vaidya, P. G. 1970 Attenuation of plane wave and higher order mode sound propagation in lined ducts. J. Sound Vib. 12 (2), 201–224.Google Scholar
Dokumaci, E. 2014 On the effect of viscosity and thermal conductivity on sound propagation in ducts: a re-visit to the classical theory with extensions for higher order modes and presence of mean flow. J. Sound Vib. 333 (21), 5583–5599.CrossRefGoogle Scholar
Eversman, W. 1973 Approximation for thin boundary layers in the sheared flow duct transmission problem. J. Acoust. Soc. Am. 53 (5), 1346–1350.Google Scholar
Eversman, W. & Beckemeyer, R. J. 1972 Transmission of sound in ducts with thin shear layer – convergence to the uniform flow case. J. Acoust. Soc. Am. 52 (1B), 216–220.Google Scholar
Gabard, G. 2013 A comparison of impedance boundary conditions for flow acoustics. J. Sound Vib. 332 (4), 714–724.Google Scholar
Greenspan, M. 1959 Rotational relaxation in nitrogen, oxygen and air. J. Acoust. Soc. Am. 31, 155–160.Google Scholar
Ingard, U. 1959 Influence of fluid motion past a plane boundary on sound reflection, absorption, and transmission. J. Acoust. Soc. Am. 31, 1035–1036.Google Scholar
Ingard, U. 2010 Noise Reduction Analysis: Infinity Science Series. Jones & Bartlett Learning.Google Scholar
Jones, M. G., Watson, W. R. & Parrott, T. L.2005 Benchmark data for evaluation of aeroacoustic propagation codes with grazing flow. AIAA Paper 2005-2853.Google Scholar
Joubert, L.2010 Asymptotic approach for the mathematical and numerical analysis of the acoustic propagation in a strong shear flow. PhD thesis, École Polytechnique.Google Scholar
Kadoya, K., Matsunaga, N. & Nagashima, A. 1985 Viscosity and thermal conductivity of dry air in the gaseous phase. J. Phys. Chem. Ref. Data 14 (4), 947–970.Google Scholar
Khamis, D. & Brambley, E. J.2015 The effective impedance of a finite-thickness viscothermal boundary layer over an acoustic lining. AIAA Paper 2015-2229.CrossRefGoogle Scholar
Khamis, D. & Brambley, E. J. 2016 Acoustic boundary conditions at an impedance lining in inviscid shear flow. J. Fluid Mech. 796, 386–416.Google Scholar
Ko, S.-H. 1971 Sound attenuation in lined rectangular ducts with flow and its application to the reduction of aircraft engine noise. Acoust. Soc. Am. J. 50, 1418–1432.Google Scholar
Ko, S.-H. 1972 Sound attenuation in acoustically lined circular ducts in the presence of uniform flow and shear flow. J. Sound Vib. 22 (2), 193–210.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn. Elsevier.Google Scholar
Marx, D. & Aurégan, Y. 2013 Effect of turbulent eddy viscosity on the unstable surface mode above an acoustic liner. J. Sound Vib. 332 (15), 3803–3820.Google Scholar
Marx, D., Aurégan, Y., Bailliet, H. & Valiére, J.-C. 2010 PIV and LDV evidence of hydrodynamic instability over a liner in a duct with flow. J. Sound Vib. 329, 3798–3812.Google Scholar
Mcalpine, A., Astley, R. J., Hii, V. J. T., Baker, N. J. & Kempton, A. J. 2006 Acoustic scattering by an axially-segmented turbofan inlet duct liner at supersonic fan speeds. J. Sound Vib. 294 (4–5), 780–806.Google Scholar
Mikhail, M. N. & El-Tantawy, M. R. 1994 The acoustic boundary layers: a detailed analysis. J. Comput. Appl. Maths 51, 15–36.Google Scholar
Mungur, P. & Gladwell, G. M. L. 1969 Acoustic wave propagation in a sheared fluid contained in a duct. J. Sound Vib. 9 (1), 28–48.Google Scholar
Myers, M. K. 1980 On the acoustic boundary condition in the presence of flow. J. Sound Vib. 71 (3), 429–434.Google Scholar
Myers, M. K. & Chuang, S. L. 1984 Uniform asymptotic approximations for duct acoustic modes in a thin boundary-layer flow. AIAA J. 22 (9), 1234–1241.Google Scholar
Nayfeh, A. H. 1973 Effect of the acoustic boundary layer on the wave propagation in ducts. J. Acoust. Soc. Am. 54, 1737–1742.CrossRefGoogle Scholar
Nayfeh, A. H., Kaiser, J. E. & Shaker, B. S. 1974 Effect of mean-velocity profile shapes on sound transmission through two-dimensional ducts. J. Sound Vib. 34 (3), 413–423.Google Scholar
Pierce, A. D. 1994 Acoustics, 3rd edn. Acoustical Society of America.Google Scholar
Pinkerton, J. M. M. 1947 A pulse method for the measurement of ultrasonic absorption in liquids: results for water. Nature 160, 128–129.Google Scholar
Pridmore-Brown, D. C. 1958 Sound propagation in a fluid flowing through an attenuating duct. J. Fluid Mech. 4 (4), 393–406.Google Scholar
Renou, Y. & Aurégan, Y.2010 On a modified myers boundary condition to match lined wall impedance deduced from several experimental methods in presence of a grazing flow. AIAA Paper 2010-3945.Google Scholar
Renou, Y. & Aurégan, Y. 2011 Failure of the Ingard–Myers boundary condition for a lined duct: an experimental investigation. J. Acoust. Soc. Am. 130 (1), 52–60.CrossRefGoogle ScholarPubMed
Rice, E. J. 1969 Propagation of waves in an acoustically lined duct with a mean flow. NASA Special Publ. 207, 345–355.Google Scholar
Rienstra, S. W. 2003 A classification of duct modes based on surface waves. Wave Motion 37 (2), 119–135.Google Scholar
Rienstra, S. W.2006 Impedance models in time domain, including the extended helmholtz resonator model. AIAA Paper 2006-2686.Google Scholar
Rienstra, S. W. & Darau, M. 2011 Boundary-layer thickness effects of the hydrodynamic instability along an impedance wall. J. Fluid Mech. 671, 559–573.Google Scholar
Stewart, H. J. 1942 The energy equation for a viscous compressible fluid. Proc. Natl Acad Sci. USA 28 (5), 161–164.Google Scholar
Tack, D. H. & Lambert, R. F. 1965 Influence of shear flow on sound attenuation in a lined duct. J. Acoust. Soc. Am. 38 (4), 655–666.Google Scholar
Tam, C. K. W., Pastouchenko, N. N., Jones, M. G. & Watson, W. R. 2014 Experimental validation of numerical simulations for an acoustic liner in grazing flow: self-noise and added drag. J. Sound Vib. 333 (13), 2831–2854.CrossRefGoogle Scholar
Tester, B. J. 1973 Some aspects of ‘sound’ attenuation in lined ducts containing inviscid mean flows with boundary layers. J. Sound Vib. 28, 217–245.Google Scholar
Tritton, D. J. 1988 Physical Fluid Dynamics: Oxford Science Publications. Oxford University Press.Google Scholar
Zhang, Q. & Bodony, D. J. 2012 Numerical investigation and modelling of acoustically excited flow through a circular orifice backed by a hexagonal cavity. J. Fluid Mech. 693, 367–401.Google Scholar
Zhang, Q. & Bodony, D. J. 2016 Numerical investigation of a honeycomb liner grazed by laminar and turbulent boundary layers. J. Fluid Mech. 792, 936–980.Google Scholar