Article contents
Viscous effects in Mach reflection of shock waves and passage to the inviscid limit
Published online by Cambridge University Press: 15 March 2023
Abstract
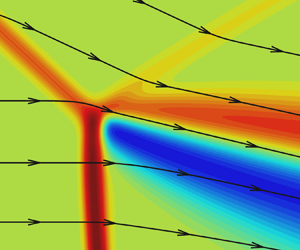
The influence of viscosity on the Mach reflection of shock waves in a steady flow of a monatomic gas is studied by solving the Navier–Stokes equations numerically. Based on the nested block grid refinement technique, the flow near the shock wave intersection is simulated, and its behaviour with increasing Reynolds number is studied. The computations are performed for the interaction of both strong (free-stream Mach number  $M_\infty = 4$) and weak (
$M_\infty = 4$) and weak ( $M_\infty = 1.7$) shock waves. In the strong reflection of shock waves at all Reynolds numbers in the examined range, it is found that there exists a small-size zone behind the shock wave intersection where the flow parameters differ from those predicted by the Rankine–Hugoniot relations and hence deviate from the predictions of the inviscid three-shock theory. The structure of this zone is self-similar: in coordinates normalised to the mean free path of molecules in the free stream. The structure is identical at all Reynolds numbers considered in the study. As the Reynolds number increases, the size of this zone in physical coordinates decreases, but the maximum difference between the viscous and inviscid solutions in this zone remains constant, reaching approximately
$M_\infty = 1.7$) shock waves. In the strong reflection of shock waves at all Reynolds numbers in the examined range, it is found that there exists a small-size zone behind the shock wave intersection where the flow parameters differ from those predicted by the Rankine–Hugoniot relations and hence deviate from the predictions of the inviscid three-shock theory. The structure of this zone is self-similar: in coordinates normalised to the mean free path of molecules in the free stream. The structure is identical at all Reynolds numbers considered in the study. As the Reynolds number increases, the size of this zone in physical coordinates decreases, but the maximum difference between the viscous and inviscid solutions in this zone remains constant, reaching approximately  $10\,\%$ for pressure. In the weak reflection of shock waves, the flow structure behind the shock wave intersection is not self-similar, i.e. the flow fields at different Reynolds numbers do not coincide in the normalised coordinates, but converge, as the Reynolds number increases, to the parameters predicted by the inviscid three-shock theory.
$10\,\%$ for pressure. In the weak reflection of shock waves, the flow structure behind the shock wave intersection is not self-similar, i.e. the flow fields at different Reynolds numbers do not coincide in the normalised coordinates, but converge, as the Reynolds number increases, to the parameters predicted by the inviscid three-shock theory.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
REFERENCES
- 6
- Cited by



