Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T13:34:26.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Unsteady thrust, lift and moment of a two-dimensional flapping thin airfoil in the presence of leading-edge vortices: a first approximation from linear potential theory

Published online by Cambridge University Press:  20 July 2018

R. Fernandez-Feria Open the ORCID record for R. Fernandez-Feria [Opens in a new window]  and
J. Alaminos-Quesada
R. Fernandez-Feria*
Affiliation:
Fluid Mechanics, Universidad de Málaga, Andalucía Tech, Dr Ortiz Ramos s/n, 29071 Málaga, Spain
J. Alaminos-Quesada
Affiliation:
Fluid Mechanics, Universidad de Málaga, Andalucía Tech, Dr Ortiz Ramos s/n, 29071 Málaga, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The effect of a leading-edge vortex (LEV) on the lift, thrust and moment of a two-dimensional heaving and pitching thin airfoil is analysed within the unsteady linear potential theory. First, general expressions that take into account the effect of any set of unsteady point vortices interacting with the oscillating foil and unsteady wake are derived. Then, a simplified analysis, based on the Brown–Michael model, of the initial stages of the growing LEV from the sharp leading edge during each half-stroke is used to obtain simple expressions for its main contribution to the unsteady lift, thrust and moment. It is found that the LEV contributes to the aerodynamic forces and moment provided that a pitching motion exists, while its effect is negligible, in the present approximation, for a pure heaving motion, and for some combined pitching and heaving motions with large phase shifts which are also characterized in the present work. In particular, the effect of the LEV is found to decrease with the distance of the pivot point from the trailing edge. Further, the time-averaged lift and moment are not modified by the growing LEVs in the present approximation, and only the time-averaged thrust force is corrected, decreasing slightly in most cases in relation to the linear potential results by an amount proportional to 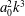$a_{0}^{2}k^{3}$ for large 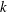$k$, where 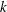$k$ is the reduced frequency and 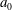$a_{0}$ is the pitching amplitude. The time-averaged input power is also modified by the LEV in the present approximation, so that the propulsion efficiency changes by both the thrust and the power, these corrections being relevant only for pivot locations behind the midchord point. Finally, the potential results modified by the LEV are compared with available experimental data.

JFM classification

Aerodynamics: Aerodynamics Vortex Flows: Vortex Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 344 - 373
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alaminos-Quesada, J. & Fernandez-Feria, R. 2017 Effect of the angle of attack on the transient lift during the interaction of a vortex with a flat plate: potential theory and experimental results. J. Fluids Struct. 74, 130–141.Google Scholar
Anderson, J. M., Streitlien, K., Barret, K. S. & Triantafyllou, M. S 1998 Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72.Google Scholar
Baik, Y. S., Bernal, L. P., Granlund, K. & Ol, M. V. 2012 Unsteady force generation and vortex dynamics of pitching and plunging aerofoils. J. Fluid Mech. 709, 37–68.Google Scholar
Brown, C. E. & Michael, W. H. 1954 Effect of leading edge separation on the lift of a delta wing. J. Aero. Sci. 21, 690–694.Google Scholar
Carrier, G. F., Krook, M. & Pearson, C. E. 2005 Functions of a Complex Variable. Theory and Technique. SIAM.Google Scholar
Cordes, U., Kampers, G., Meissner, T., Tropea, C., Pinke, J. & Hölling, M. 2017 Note on the limitations of the Theodorsen and Sears functions. J. Fluid Mech. 811, R1.Google Scholar
Dickinson, M. H. & Götz, K. G. 1993 Unsteady aerodynamics performance of model wings at low Reynolds numbers. J. Exp. Biol. 174, 45–64.Google Scholar
Ellington, C. P. 1984 The aerodynamics of hovering insect flight. Part IV. Aeorodynamic mechanisms. Phil. Trans. R. Soc. Lond. B 305, 79–113.Google Scholar
Ellington, C. P., van den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384, 626–630.Google Scholar
Fernandez-Feria, R. 2016 Linearized propulsion theory of flapping airfoils revisited. Phys. Rev. Fluids 1, 084502.Google Scholar
Fernandez-Feria, R. 2017 Note on optimum propulsion of heaving and pitching airfoils from linear potential theory. J. Fluid Mech. 826, 781–796.Google Scholar
Garrick, I. E.1936 Propulsion of a flapping and oscillating airfoil. NACA Tech. Rep. TR 567.Google Scholar
Garrick, I. E.1938 On some reciprocal relations in the theory of nonstationary flows. NACA Tech. Rep. TR 629.Google Scholar
Graham, J. M. R. 1983 The lift on an aerofoil in starting flow. J. Fluid Mech. 133, 413–425.Google Scholar
Graham, W. R., Pitt Ford, C. W. & Babinsky, H. 2017 An impulse-based approach to estimating forces in unsteady flow. J. Fluid Mech. 815, 60–76.Google Scholar
Hemati, M. S., Eldredge, J. D. & Speyer, J. L. 2014 Improving vortex models via optimal control theory. J. Fluids Struct. 49, 91–111.Google Scholar
Howe, M. S. 1996 Emendation of the Brown and Michael equation, with application to sound generation by vortex motion near a half-plane. J. Fluid Mech. 329, 89–101.Google Scholar
Jones, M. A. 2003 The separated flow of an inviscid fluid around a moving flat plate. J. Fluid Mech. 496, 405–441.Google Scholar
von Kármán, T. & Sears, W. R. 1938 Airfoil theory for non-uniform motion. J. Aero. Sci. 5, 370–390.Google Scholar
Li, J., Bai, C.-Y. & Wu, Z.-N. 2015 A two-dimensional multibody integral approach for forces in inviscid flow with free vortices and vortex production. J. Fluids Engng 137, 021205.Google Scholar
Li, J. & Wu, Z. N. 2015 Unsteady lift for the Wagner problem in the presence of additional leading/trailing edge vortices. J. Fluid Mech. 769, 182–217.Google Scholar
Li, J. & Wu, Z. N. 2016 A vortex force study for a flat plate at high angle of attack. J. Fluid Mech. 801, 222–249.Google Scholar
Mackowski, A. W. & Williamson, H. K. 2015 Direct measurement of thrust and efficiency of an airfoil undergoing pure pitching. J. Fluid Mech. 765, 524–543.Google Scholar
Mackowski, A. W. & Williamson, H. K. 2017 Effect of pivot point location and passive heave on propulsion from a pitching airfoil. Phys. Rev. Fluids 2, 013101.Google Scholar
Martín-Alcántara, A., Fernandez-Feria, R. & Sanmiguel-Rojas, E. 2015 Vortex flow structures and interactions for the optimum thrust efficiency of a heaving airfoil at different mean angles of attack. Phys. Fluids 27, 073602.Google Scholar
Maxworthy, T. 2007 The formation and maintenance of a leading-edge vortex during the forward motion of an animal wing. J. Fluid Mech. 587, 471–475.Google Scholar
McGowan, G. Z., Granlund, K., Ol, M. V., Gopalarathnam, A. & Edwards, J. R. 2011 Investigations of lift-based pitch–plunge equivalence for airfoils at low Reynolds numbers. AIAA J. 49, 1511–1524.Google Scholar
Michelin, S. & Llewellyn Smith, S. G. 2009 An unsteady point vortex method for coupled fluid–solid problems. Theor. Comput. Fluid Dyn. 23, 127–153.Google Scholar
Minotti, F. O. 2002 Unsteady two-dimensional theory of a flapping wing. Phys. Rev. E 66, 051907.Google Scholar
Newman, J. N. 1977 Marine Hydrodynamics. MIT Press.Google Scholar
Olver, F. W. J. & Maximon, L. C. 2010 Bessel functions. In NIST Handbook of Mathematical Functions (ed. Olver, F. W. J., Lozier, D. W., Boisvert, R. F. & Clark, C. W.), pp. 215–286. National Institute of Standards and Technology.Google Scholar
Pitt Ford, C. W. & Babinsky, H. 2013 Lift and the leading-edge vortex. J. Fluid Mech. 720, 280–313.Google Scholar
Pullin, D. I. & Wang, Z. J. 2004 Unsteady forces on an accelerating plate and application to hovering insect flight. J. Fluid Mech. 509, 1–21.Google Scholar
Ramesh, K., Gopalarathnam, A., Edwards, J. R., Ol, M. V. & Granlund, K. 2013 An unsteady airfoil theory applied to pitching motions validated against experiment and computation. Theor. Comput. Fluid Dyn. 27, 843–864.Google Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Shyy, W. & Liu, H. 2007 Flapping wings and aerodynamic lift: the role of the leading-edge vortex. AIAA J. 45, 2817–2819.Google Scholar
Tchieu, A. A. & Leonard, A. 2011 A discrete-vortex model for the arbitrary motion of a thin airfoil with fluidic control. J. Fluids Struct. 27, 680–693.Google Scholar
Theodorsen, T.1935 General theory of aerodynamic instability and the mechanism of flutter. NACA Tech. Rep. TR 496.Google Scholar
Wang, C. & Eldredge, J. D. 2013 Low-order phenomenological modeling of leading-edge vortex formation. Theor. Comput. Fluid Dyn. 27, 577–598.Google Scholar
Wang, Z. J. 2000 Vortex shedding and frequency selection in flapping fight. J. Fluid Mech. 410, 323–341.Google Scholar
Wang, Z. J. 2005 Dissecting insect flight. Annu. Rev. Fluid Mech. 37, 183–210.Google Scholar
Wu, J. C. 1981 Theory for the aerodynamic force and moment in viscous flows. AIAA J. 19, 432–441.Google Scholar
Wu, J.-Z., Ma, H.-Y. & Zhou, M.-D. 2006 Vorticity and Vortex Dynamics. Springer.Google Scholar
Xia, X. & Mohseni, K. 2013 Lift evaluation of a two-dimensional pitching flat plate. Phys. Fluids 25, 091901.Google Scholar
Xia, X. & Mohseni, K. 2017 Unsteady aerodynamics of vortex-sheet formulation of a two-dimensional airfoil. J. Fluid Mech. 830, 439–478.Google Scholar