Hostname: page-component-5cf477f64f-bmd9x Total loading time: 0 Render date: 2025-04-07T02:26:40.910Z Has data issue: false hasContentIssue false
  • English
  • Français

Unsteady sheet fragmentation: droplet sizes and speeds

Published online by Cambridge University Press:  13 June 2018

Y. Wang  and
L. Bourouiba Open the ORCID record for L. Bourouiba [Opens in a new window]
Y. Wang
Affiliation:
The Fluid Dynamics of Disease Transmission Laboratory, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
L. Bourouiba*
Affiliation:
The Fluid Dynamics of Disease Transmission Laboratory, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Understanding what shapes the drop size distributions produced from fluid fragmentation is important for a range of industrial, natural and health processes. Gilet & Bourouiba (J. R. Soc. Interface, vol. 12, 2015, 20141092) showed that both the size and speed of fragmented droplets are critical to transmission of pathogens in the agricultural context. In this paper, we study both the size and speed distributions of droplets ejected during a canonical unsteady sheet fragmentation from drop impact on a target of comparable size to that of the drop. Upon impact, the drop transforms into a sheet which expands in the air bounded by a rim on which ligaments grow, continuously shedding droplets. We developed high-precision tracking algorithms that capture all ejected droplets, measuring their size and speed, as well as the detachment time from, and link to, their ligament of origin. Both size and speed distributions of all ejected droplets are skewed. We show that the polydispersity and skewness of the distributions are inherently due to the unsteadiness of the sheet expansion. We show that each ligament sheds a single drop at a time throughout the entire sheet expansion by a mechanism of end-pinching. 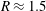The droplet-to-ligament size ratio $R\approx 1.5$ remains constant throughout the unsteady fragmentation, and is robust to change in impact Weber number. We also show that the population mean speed of the fragmented droplets at a given time is equal to the population mean speed of ligaments one necking time prior to detachment time.

JFM classification

Drops and Bubbles: Aerosols/atomization Drops and Bubbles: Drops Instability: Instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 848 , 10 August 2018 , pp. 946 - 967
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bourouiba, L., Dehandschoewercker, E. & Bush, J. W. M. 2014 Violent expiratory events: on coughing and sneezing. J. Fluid Mech. 745, 537–563.Google Scholar
Clanet, C. & Lasheras, J. C. 1999 Transition from dripping to jetting. J. Fluid Mech. 383, 307–326.Google Scholar
Clanet, C. & Villermaux, E. 2002 Life of a smooth liquid sheet. J. Fluid Mech. 462, 307–340.CrossRefGoogle Scholar
Culick, F. E. C. 1960 Comments on a Ruptured Soap Film. J. Appl. Phys. 31, 1128–1129.CrossRefGoogle Scholar
Eggers, J. & Dupont, T. F. 1994 Drop formation in a one-dimensional approximation of the Navier–Stokes equation. J. Fluid Mech. 262, 205–221.Google Scholar
Eggers, J., Fontelos, M. A., Josserand, C. & Zaleski, S. 2010 Drop dynamics after impact on a solid wall: theory and simulations. Phys. Fluids 22, 1–13.Google Scholar
Fantini, E., Tognotti, L. & Tonazzini, A. 1990 Drop size distribution in sprays by image processing. Comput. Chem. Engng 14, 1201–1211.Google Scholar
Gilet, T. & Bourouiba, L. 2014 Rain-induced ejection of pathogens from leaves: revisiting the hypothesis of splash-on-film using high-speed visualization. Integr. Compar. Biol. 54, 974–984.Google Scholar
Gilet, T. & Bourouiba, L. 2015 Fluid fragmentation shapes rain-induced foliar disease transmission. J. R. Soc. Interface 12, 20141092.Google Scholar
Gordillo, J. M. & Gekle, S. 2010 Generation and breakup of Worthington jets after cavity collapse. Part 2. Tip breakup of stretched jets. J. Fluid Mech. 663, 331–346.Google Scholar
Gordillo, J. M., Lhuissier, H. & Villermaux, E. 2014 On the cusps bordering liquid sheets. J. Fluid Mech. 754, R1.Google Scholar
Gordillo, J. M. & Perez-Sborid, M. 2005 Aerodynamic effects in the break-up of liquid jets: on the first wind-induced break-up regime. J. Fluid Mech. 541, 1–20.Google Scholar
Hoepffner, J. & Paré, G. 2013 Recoil of a liquid filament: escape from pinch-off through creation of a vortex ring. J. Fluid Mech. 734, 183–197.Google Scholar
Josserand, C. & Thoroddsen, S. T. 2016 Drop impact on a solid surface. Annu. Rev. Fluid Mech. 48, 365–391.Google Scholar
Keller, J. B. 1983 Breaking of liquid films and threads. Phys. Fluids 26, 3451–3453.CrossRefGoogle Scholar
Lastakowski, H., Boyer, F., Biance, A. L., Pirat, C. & Ybert, C. 2014 Bridging local to global dynamics of drop impact onto solid substrates. J. Fluid Mech. 747, 103–118.Google Scholar
Peters, I. R., van der Meer, D. & Gordillo, J. M. 2013 Splash wave and crown breakup after disc impact on a liquid surface. J. Fluid Mech. 724, 553–580.Google Scholar
Rayleigh, Lord 1878 On the instability of jets. Proc. R. Soc. Lond. A s1‐10, 4–13.Google Scholar
Riboux, G. & Gordillo, J. M. 2015 The diameters and velocities of the droplets ejected after splashing. J. Fluid Mech. 772, 630–648.Google Scholar
Rioboo, R., Marengo, M. & Tropea, C. 2002 Time evolution of liquid drop impact onto solid, dry surfaces. Exp. Fluids 33, 112–124.CrossRefGoogle Scholar
Roisman, I. V., Berberovi, E. & Tropea, C. 2009 Inertia dominated drop collisions. I. On the universal flow in the lamella. Phys. Fluids 21, 052103.CrossRefGoogle Scholar
Rozhkov, A., Prunet-Foch, B. & Vignes-Adler, M. 2002 Impact of water drops on small targets. Phys. Fluids 14, 3485–3501.Google Scholar
Rozhkov, A., Prunet-Foch, B. & Vignes-Adler, M. 2004 Dynamics of a liquid lamella resulting from the impact of a water drop on a small target. Proc. R. Soc. Lond. A 460, 2681–2704.Google Scholar
Savart, F. 1833a Me?moire sur le choc dune veine liquide lance?e sur un plan circulaire. Ann. Chim. 54, 56–87.Google Scholar
Savart, F. 1833b Suite du me?moire sur le choc dune veine liquide lance?e sur un plan circulaire. Ann. Chim. 54, 113–145.Google Scholar
Savva, N. & Bush, J. W. M. 2009 Viscous sheet retraction. J. Fluid Mech. 626, 211–240.Google Scholar
Scharfman, B. E., Techet, A. H., Bush, J. W. M. & Bourouiba, L. 2016 Visualization of sneeze ejecta: steps of fluid fragmentation leading to respiratory droplets. Exp. Fluids 57, 24.Google Scholar
Schulkes, R. M. S. M. 1996 The contraction of liquid filaments. J. Fluid Mech. 309, 277–300.Google Scholar
Sterling, A. M. & Sleicher, C. A. 1975 The instability of capillary jets. J. Fluid Mech. 68, 477–495.Google Scholar
Thoroddsen, S. T., Takehara, K. & Etoh, T. G. 2012 Micro-splashing by drop impacts. J. Fluid Mech. 706, 560–570.Google Scholar
Ting, L. & Keller, J. B. 1990 Slender jets and thin sheets with surface tension. SIAM J. Appl. Math. 50 (6), 1533–1546.Google Scholar
Villermaux, E. 2007 Fragmentation. Annu. Rev. Fluid Mech. 39, 419–446.CrossRefGoogle Scholar
Villermaux, E. & Bossa, B. 2011 Drop fragmentation on impact. J. Fluid Mech. 668, 412–435.Google Scholar
Villermaux, E., Marmottant, Ph. & Duplat, J. 2004 Ligament-mediated spray formation. Phys. Rev. Lett. 92, 074501.CrossRefGoogle ScholarPubMed
Wang, Y. & Bourouiba, L. 2017 Drop impact on small surfaces: thickness and velocity profiles of the expanding sheet in the air. J. Fluid Mech. 814, 510–534.CrossRefGoogle Scholar
Wang, Y. & Bourouiba, L. 2018 Non-isolated drop impact on surfaces. J. Fluid Mech. 835, 24–44.Google Scholar
Yarin, A. L. 2006 Drop impact dynamics: splashing, spreading, receding, bouncing…. Annu. Rev. Fluid Mech. 38, 159–192.Google Scholar
Yarin, A. L. & Weiss, D. A. 1995 Impact of drops on solid surfaces: self-similar capillary waves, and splashing as a new type of kinematic discontinuity. J. Fluid Mech. 283, 141–173.CrossRefGoogle Scholar