Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-27T08:22:39.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Universal statistics of point vortex turbulence

Published online by Cambridge University Press:  14 August 2015

J. G. Esler  and
T. L. Ashbee
J. G. Esler*
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK
T. L. Ashbee
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A new methodology, based on the central limit theorem, is applied to describe the statistical mechanics of two-dimensional point vortex motion in a bounded container 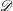$\mathscr{D}$, as the number of vortices 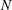$N$ tends to infinity. The key to the approach is the identification of the normal modes of the system with the eigenfunction solutions of the so-called hydrodynamic eigenvalue problem of the Laplacian in 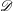$\mathscr{D}$. The statistics of the projection of the vorticity distribution onto these eigenfunctions (‘vorticity projections’) are then investigated. The statistics are used first to obtain the density-of-states function and caloric curve for the system, generalising previous results to arbitrary (neutral) distributions of vortex circulations. Explicit expressions are then obtained for the microcanonical (i.e. fixed energy) probability density functions of the vorticity projections in a form that can be compared directly with direct numerical simulations of the dynamics. The energy spectra of the resulting flows are predicted analytically. Ensembles of simulations with 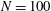$N=100$, in several conformal domains, are used to make a comprehensive validation of the theory, with good agreement found across a broad range of energies. The probability density function of the leading vorticity projection is of particular interest because it has a unimodal distribution at low energy and a bimodal distribution at high energy. This behaviour is indicative of a phase transition, known as Onsager–Kraichnan condensation in the literature, between low-energy states with no mean flow in the domain and high-energy states with a coherent mean flow. The critical temperature for the phase transition, which depends on the shape but not the size of 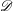$\mathscr{D}$, and the associated critical energy are found. Finally the accuracy and the extent of the validity of the theory, at finite 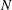$N$, are explored using a Markov chain phase-space sampling method.

JFM classification

Mathematical Foundations: Mathematical Foundations Turbulent Flows: Turbulence theory Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 779 , 25 September 2015 , pp. 275 - 308
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashbee, T. L.2014 Dynamics and statistical mechanics of point vortices in bounded domains. PhD thesis, University College London.Google Scholar
Ashbee, T. L., Esler, J. G. & McDonald, N. R. 2013 Generalized Hamiltonian point vortex dynamics on arbitrary domains using the method of fundamental solutions. J. Comput. Phys. 246, 289–303.CrossRefGoogle Scholar
Bausch, J. 2013 On the efficient calculation of a linear combination of chi-square random variables with an application in counting string vacua. J. Phys. A: Math. Theor. 46, 505202.CrossRefGoogle Scholar
Benzi, R., Colella, M., Briscolini, M. & Santangelo, P. 1992 A simple point vortex model for two-dimensional decaying turbulence. Phys. Fluids 4, 1036–1039.CrossRefGoogle Scholar
Berg, B. A. 2000 Introduction to multicanonical Monte Carlo simulations. Fields Inst. Commun. 26, 1–24.Google Scholar
Billam, T. P., Reeves, M. T., Anderson, B. P. & Bradley, A. S. 2014 Onsager–Kraichnan condensation in decaying two-dimensional quantum turbulence. Phys. Rev. Lett. 112, 145301.CrossRefGoogle ScholarPubMed
Book, D. L., Fisher, S. & McDonald, B. E. 1975 Steady-state distributions of interacting discrete vortices. Phys. Rev. Lett. 34, 4–8.CrossRefGoogle Scholar
Bos, W. J. T., Neffaa, S. & Schneider, K. 2008 Rapid generation of angular momentum in bounded magnetized plasma. Phys. Rev. Lett. 101, 235003.CrossRefGoogle ScholarPubMed
Bradley, A. S. & Anderson, B. P. 2012 Energy spectra of vortex distributions in two-dimensional quantum turbulence. Phys. Rev. X 2, 041001.Google Scholar
Bühler, O. 2002 Statistical mechanics of strong and weak point vortices in a cylinder. Phys. Fluids 14 (7), 2139–2149.CrossRefGoogle Scholar
Campa, A., Dauxois, T. & Ruffo, S. 2009 Statistical mechanics and dynamics of solvable models with long-range interactions. Phys. Rep. 480, 57–159.CrossRefGoogle Scholar
Campbell, L. J. & O’Neil, K. 1991 Statistics of two-dimensional point vortices and high-energy vortex states. J. Stat. Phys. 65, 495–529.CrossRefGoogle Scholar
Chavanis, P.-H. & Sommeria, J. 1996 Classification of self-organized vortices in two-dimensional turbulence: the case of a bounded domain. J. Fluid Mech. 314, 267–297.CrossRefGoogle Scholar
Chertkov, M., Connaughton, C., Kolokolov, I. & Lebedev, V. 2007 Dynamics of energy condensation in two-dimensional turbulence. Phys. Rev. Lett. 99, 084501.CrossRefGoogle ScholarPubMed
Clercx, H. J. H., Maassen, S. R. & van Heijst, G. J. F. 1998 Spontaneous spin-up during the decay of 2D turbulence in a square container with rigid boundaries. Phys. Rev. Lett. 80, 5129–5132.CrossRefGoogle Scholar
Clercx, H. J. H., Nielsen, A. H., Torres, D. J. & Coutsias, E. A. 2001 Two-dimensional turbulence in square and circular domains with no-slip walls. Eur. J. Mech. (B/Fluids) 20 (4), 557–576.CrossRefGoogle Scholar
Creutz, M. 1983 Microcanonical Monte Carlo simulation. Phys. Rev. Lett. 50, 1411–1414.CrossRefGoogle Scholar
Debnath, L. & Mikusiński, P. 2005 Introduction to Hilbert Spaces with Applications, 3rd edn. Elsevier.Google Scholar
Driscoll, T. A. & Maki, K. L. 2007 Searching for rare growth factors using multicanonical Monte Carlo methods. SIAM Rev. 49, 673–692.CrossRefGoogle Scholar
Dritschel, D. G., Lucia, M. & Poje, A. C. 2015 Equilibrium statistics and dynamics of point vortex flows on the sphere. Phys. Rev. E 91, 063014.CrossRefGoogle Scholar
Dritschel, D. G., Scott, R. K., Macaskill, C., Gottwald, G. A. & Tran, C. V. 2008 Unifying scaling theory for vortex dynamics in two-dimensional turbulence. Phys. Rev. Lett. 101, 094501.CrossRefGoogle ScholarPubMed
Edwards, S. F. & Taylor, J. B. 1974 Negative temperature states of two-dimensional plasmas and vortex fluids. Proc. R. Soc. A 336 (1606), 257–271.Google Scholar
Esler, J. G., Ashbee, T. L. & McDonald, N. R. 2013 Statistical mechanics of a neutral point-vortex gas at low energy. Phys. Rev. E 88, 012109.CrossRefGoogle ScholarPubMed
Eyink, G. L. & Sreenivasan, K. R. 2006 Onsager and the theory of hydrodynamic turbulence. Rev. Mod. Phys. 78, 87–135.CrossRefGoogle Scholar
Flucher, M. & Gustafsson, B. 1999 Vortex Motion in Two Dimensional Hydrodynamics. Springer.CrossRefGoogle Scholar
Joyce, G. & Montgomery, D. 1973 Negative temperature states for a two-dimensional guiding center plasma. J. Plasma Phys. 10, 107–121.CrossRefGoogle Scholar
Kiessling, M. K.-H. 1995 Negative temperature bounds for 2D vorticity compounds. Lett. Math. Phys. 34, 49–57.CrossRefGoogle Scholar
Kunin, I. A., Hussain, F. & Zhou, X. 1994 Dynamics of a pair of vortices in a rectangle. Intl J. Engng Sci. 32 (12), 1835–1844.CrossRefGoogle Scholar
Lin, C. C. 1941a On the motion of vortices in two dimensions. I: Existence of the Kirchhoff–Routh function. Proc. Natl Acad. Sci. USA 27, 570–575.CrossRefGoogle ScholarPubMed
McDonald, B. E. 1974 Numerical calculation of nonunique solutions of a two-dimensional sinh-Poisson equation. J. Comput. Phys. 16 (4), 360–370.CrossRefGoogle Scholar
Miller, J. 1990 Statistical mechanics of the Euler equation in two dimensions. Phys. Rev. Lett. 65, 2137–2140.CrossRefGoogle ScholarPubMed
Naso, A., Chavanis, P.-H. & Dubrulle, B. 2010 Statistical mechanics of two-dimensional Euler flows and minimum enstrophy states. Eur. Phys. J. B 77 (2), 187–212.CrossRefGoogle Scholar
Neely, T. W., Bradley, A. S., Samson, E. C., Rooney, S. J., Wright, E. M., Law, K. J. H., Carretero-González, R., Kevrekidis, P. G., Davis, M. J. & Anderson, B. P. 2013 Characteristics of two-dimensional quantum turbulence in a compressible superfluid. Phys. Rev. Lett. 111, 235301.CrossRefGoogle Scholar
Newton, P. K. 2001 The N-Vortex Problem: Analytical Techniques. Springer.CrossRefGoogle Scholar
Onsager, L. 1949 Statistical hydrodynamics. Nuovo Cimento 6, 279–287.CrossRefGoogle Scholar
Paret, J. & Tabeling, P. 1998 Intermittency in the two-dimensional inverse cascade of energy: experimental observations. Phys. Fluids 10, 3126–3136.CrossRefGoogle Scholar
Pointin, Y. B. & Lundgren, T. S. 1976 Statistical mechanics of two-dimensional vortices in a bounded container. Phys. Fluids 19 (10), 1459–1470.CrossRefGoogle Scholar
Richardson, S. 1981 Some Hele-Shaw flows with time-dependent free boundaries. J. Fluid Mech. 102, 263–278.CrossRefGoogle Scholar
Robert, R. 1991 A maximum entropy principle for two-dimensional Euler equations. J. Stat. Phys. 65, 531–553.CrossRefGoogle Scholar
Shats, M. G., Xia, H. & Punzmann, H. 2005 Spectral condensation of turbulence in plasmas and fluids and its role in low-to-high phase transitions in toroidal plasma. Phys. Rev. E 71, 046409.CrossRefGoogle ScholarPubMed
Simula, T., Davis, M. J. & Helmerson, K. 2014 Emergence of order from turbulence in an isolated planar superfluid. Phys. Rev. Lett. 113, 165302.CrossRefGoogle Scholar
Smith, R. A. 1989 Phase transition behavior in a negative-temperature guiding-center plasma. Phys. Rev. Lett. 63, 1479–1482.CrossRefGoogle Scholar
Taylor, J. B., Borchardt, M. & Helander, P. 2009 Interacting vortices and spin-up in two-dimensional turbulence. Phys. Rev. Lett. 102, 124505.CrossRefGoogle ScholarPubMed
Touchette, H. 2009 The large deviation approach to statistical mechanics. Phys. Rep. 478 (1–3), 1–69.CrossRefGoogle Scholar
Trefethen, L. N. 2000 Spectral Methods in MATLAB. SIAM.CrossRefGoogle Scholar
Weiss, J. B. & McWilliams, J. C. 1991 Nonergodicity of point vortices. Phys. Fluids A 3 (5), 835–844.CrossRefGoogle Scholar
Xiao, Z., Wan, M., Chen, S. & Eyink, G. L. 2009 Physical mechanism of the inverse energy cascade of two-dimensional turbulence: a numerical investigation. J. Fluid Mech. 619, 1–44.CrossRefGoogle Scholar