Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-02T18:01:52.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Universal fluctuations in the bulk of Rayleigh–Bénard turbulence

Published online by Cambridge University Press:  06 September 2019

Yi-Chao Xie Open the ORCID record for Yi-Chao Xie [Opens in a new window] ,
Bu-Ying-Chao Cheng ,
Yun-Bing Hu  and
Ke-Qing Xia Open the ORCID record for Ke-Qing Xia [Opens in a new window]
Yi-Chao Xie*
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, PR China Center for Complex Flows and Soft Matter Research & Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, 518055, PR China
Bu-Ying-Chao Cheng
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, PR China
Yun-Bing Hu
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, PR China Center for Complex Flows and Soft Matter Research & Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, 518055, PR China
Ke-Qing Xia*
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, PR China Center for Complex Flows and Soft Matter Research & Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, 518055, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an investigation of the root-mean-square (r.m.s.) temperature 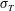$\unicode[STIX]{x1D70E}_{T}$ and the r.m.s. velocity 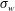$\unicode[STIX]{x1D70E}_{w}$ in the bulk of Rayleigh–Bénard turbulence, using new experimental data from the current study and experimental and numerical data from previous studies. We find that, once scaled by the convective temperature 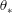$\unicode[STIX]{x1D703}_{\ast }$, the value of 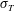$\unicode[STIX]{x1D70E}_{T}$ at the cell centre is a constant (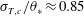$\unicode[STIX]{x1D70E}_{T,c}/\unicode[STIX]{x1D703}_{\ast }\approx 0.85$) over a wide range of the Rayleigh number (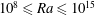$10^{8}\leqslant Ra\leqslant 10^{15}$) and the Prandtl number (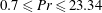$0.7\leqslant Pr\leqslant 23.34$), and is independent of the surface topographies of the top and bottom plates of the convection cell. A constant close to unity suggests that 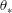$\unicode[STIX]{x1D703}_{\ast }$ is a proper measure of the temperature fluctuation in the core region. On the other hand, 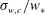$\unicode[STIX]{x1D70E}_{w,c}/w_{\ast }$, the vertical r.m.s. velocity at the cell centre scaled by the convective velocity 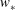$w_{\ast }$, shows a weak 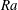$Ra$-dependence (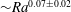${\sim}Ra^{0.07\pm 0.02}$) over 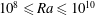$10^{8}\leqslant Ra\leqslant 10^{10}$ at 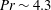$Pr\sim 4.3$ and is independent of plate topography. Similar to a previous finding by He & Xia (Phys. Rev. Lett., vol. 122, 2019, 014503), we find that the r.m.s. temperature profile 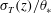$\unicode[STIX]{x1D70E}_{T}(z)/\unicode[STIX]{x1D703}_{\ast }$ in the region of the mixing zone with a mean horizontal shear exhibits a power-law dependence on the distance $z$ from the plate, but now the universal profile applies to both smooth and rough surface topographies and over a wider range of 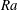$Ra$. The vertical r.m.s. velocity profile 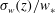$\unicode[STIX]{x1D70E}_{w}(z)/w_{\ast }$ obeys a logarithmic dependence on $z$. The study thus demonstrates that the typical scales for the temperature and the velocity are the convective temperature 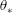$\unicode[STIX]{x1D703}_{\ast }$ and the convective velocity 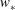$w_{\ast }$, respectively. Finally, we note that 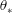$\unicode[STIX]{x1D703}_{\ast }$ may be utilised to study the flow regime transitions in ultrahigh-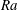$Ra$-number turbulent convection.

JFM classification

Turbulent Flows: Turbulent convection
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 878 , 10 November 2019 , R1
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 1996 Variation of temperature and velocity fluctuations in turbulent thermal convection over horizontal surfaces. Intl J. Heat Mass Transfer 39, 2303–2310.Google Scholar
Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X., Lohse, D., Stevens, R. J. A. M. & Verzicco, R. 2012 Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 114501.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.Google Scholar
Daya, Z. A. & Ecke, R. E. 2001 Does turbulent convection feel the shape of the container? Phys. Rev. Lett. 87, 184501.Google Scholar
Deardorff, J. W. 1970 Convective velocity and temperature scales for the unstable planetary boundary layer and for Rayleigh convection. J. Atmos. Sci. 27, 1211–1213.Google Scholar
Du, Y. B. & Tong, P. 2000 Turbulent thermal convection in a cell with ordered rough boundaries. J. Fluid Mech. 407, 57–84.Google Scholar
Du, Y. B. & Tong, P. 2001 Temperature fluctuations in a convection cell with rough upper and lower surfaces. Phys. Rev. E 63, 046303.Google Scholar
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16, 4462–4472.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.Google Scholar
He, Y.-H. & Xia, K.-Q. 2019 Temperature fluctuation profiles in turbulent thermal convection: a logarithmic dependence versus a power-law dependence. Phys. Rev. Lett. 122, 014503.Google Scholar
Heslot, F., Castaing, B. & Libchaber, A. 1987 Transitions to turbulence in helium gas. Phys. Rev. A 36, 5870–5873.Google Scholar
Kaczorowski, M., Chong, K.-L. & Xia, K.-Q. 2014 Turbulent flow in the bulk of Rayleigh–Bénard convection: aspect-ratio dependence of the small-scale properties. J. Fluid Mech. 747, 73–102.Google Scholar
Lakkaraju, R., Stevens, R. J. A. M., Verzicco, R., Grossmann, S., Prosperetti, A., Sun, C. & Lohse, D. 2012 Spatial distribution of heat flux and fluctuations in turbulent Rayleigh–Bénard convection. Phys. Rev. E 86, 056315.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Lui, S.-L. & Xia, K.-Q. 1998 Spatial structure of the thermal boundary layer in turbulent convection. Phys. Rev. E 57, 5494–5503.Google Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.Google Scholar
Qiu, X. L., Shang, X.-D., Tong, P. & Xia, K.-Q. 2004 Velocity oscillations in turbulent Rayleigh–Bénard convection. Phys. Fluids 16, 412–423.Google Scholar
Scheel, J. D. & Schumacher, J. 2016 Global and local statistics in turbulent convection at low Prandtl numbers. J. Fluid Mech. 802, 147–173.Google Scholar
Shang, X.-D., Tong, P. & Xia, K.-Q. 2008 Scaling of the local convective heat flux in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 100, 244503.Google Scholar
Shen, Y., Xia, K.-Q. & Tong, P. 1995 Measured local-velocity fluctuations in turbulent convection. Phys. Rev. Lett. 75, 437–440.Google Scholar
Sun, C., Cheung, Y.-H. & Xia, K.-Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.Google Scholar
Wang, J. & Xia, K.-Q. 2003 Spatial variations of the mean and statistical quantities in the thermal boundary layers of turbulent convection. Eur. Phys. J. B 32, 127–136.Google Scholar
Wang, Y., Xu, W., He, X., Yik, H., Wang, X., Schumacher, J. & Tong, P. 2018 Boundary layer fluctuations in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 840, 408–431.Google Scholar
Wei, P. & Ahlers, G. 2016 On the nature of fluctuations in turbulent Rayleigh–Bénard convection at large Prandtl numbers. J. Fluid Mech. 802, 203–244.Google Scholar
Wei, P., Chan, T.-S., Ni, R., Zhao, X.-Z. & Xia, K.-Q. 2014 Heat transport properties of plates with smooth and rough surfaces in turbulent thermal convection. J. Fluid Mech. 740, 28–46.Google Scholar
Xia, K.-Q. 2013 Current trends and future directions in turbulent thermal convection. Theor. Appl. Mech. Lett. 3, 052001.Google Scholar
Xia, K.-Q., Lam, S. & Zhou, S.-Q. 2002 Heat-flux measurement in high-Prandtl-number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88, 064501.Google Scholar
Xie, Y.-C., Ding, G.-Y. & Xia, K.-Q. 2018 Flow topology transition via global bifurcation in thermally driven turbulence. Phys. Rev. Lett. 120, 214501.Google Scholar
Xie, Y.-C. & Xia, K.-Q. 2017 Turbulent thermal convection over rough plates with varying roughness geometries. J. Fluid Mech. 825, 573–599.Google Scholar