Published online by Cambridge University Press: 04 June 2014
Closed-form solutions describing the behaviour of two-dimensional planar turbulent rising plumes and fountains from horizontal planar area and line sources in unconfined quiescent environments of uniform density are proposed. Extending the analysis on axisymmetric releases by van den Bremer & Hunt (J. Fluid Mech., vol. 644, 2010, pp. 165–192) to planar releases, the local flux balance parameter 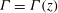 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\varGamma =\varGamma (z)$ is instrumental in describing the bulk behaviour of steady Boussinesq and non-Boussinesq planar plumes and the initial rise behaviour of Boussinesq planar fountains as a function of height
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\varGamma =\varGamma (z)$ is instrumental in describing the bulk behaviour of steady Boussinesq and non-Boussinesq planar plumes and the initial rise behaviour of Boussinesq planar fountains as a function of height  $z$. Expressions for the asymptotic virtual source correction are developed and the results elucidated by ‘scale diagrams’ (cf. Morton & Middleton, J. Fluid Mech., vol. 58, 1973, pp. 165–176) showing certain characteristic heights for different source conditions. These diagrams capture all the different manifestations of plume behaviour, encompassing fountains, jets, source-momentum-dominated or ‘forced’ plumes, pure plumes and source-buoyancy-dominated or ‘lazy’ plumes, and their associated key features. Other flow features identified include a gravity-driven deceleration regime and a mixing-driven regime for forced fountains. Deceleration in lazy fountains is purely gravity-driven. The results can be shown to be valid for both Boussinesq and non-Boussinesq plumes (but not for non-Boussinesq fountains) thus resulting in universal solutions valid for both cases provided the entrainment velocity is unaffected by non-Boussinesq effects. This paper presents and explores these universal solutions. An accompanying paper (van den Bremer & Hunt, J. Fluid Mech., vol. 750, 2014, pp. 245–258) examines the implications for non-Boussinesq plumes. The existing solutions of Lee & Emmons (J. Fluid Mech., vol. 11, 1961, pp. 353–368) generalized herein are valid for a constant entrainment coefficient
$z$. Expressions for the asymptotic virtual source correction are developed and the results elucidated by ‘scale diagrams’ (cf. Morton & Middleton, J. Fluid Mech., vol. 58, 1973, pp. 165–176) showing certain characteristic heights for different source conditions. These diagrams capture all the different manifestations of plume behaviour, encompassing fountains, jets, source-momentum-dominated or ‘forced’ plumes, pure plumes and source-buoyancy-dominated or ‘lazy’ plumes, and their associated key features. Other flow features identified include a gravity-driven deceleration regime and a mixing-driven regime for forced fountains. Deceleration in lazy fountains is purely gravity-driven. The results can be shown to be valid for both Boussinesq and non-Boussinesq plumes (but not for non-Boussinesq fountains) thus resulting in universal solutions valid for both cases provided the entrainment velocity is unaffected by non-Boussinesq effects. This paper presents and explores these universal solutions. An accompanying paper (van den Bremer & Hunt, J. Fluid Mech., vol. 750, 2014, pp. 245–258) examines the implications for non-Boussinesq plumes. The existing solutions of Lee & Emmons (J. Fluid Mech., vol. 11, 1961, pp. 353–368) generalized herein are valid for a constant entrainment coefficient  $\alpha $. New results for an entrainment coefficient that varies linearly with
$\alpha $. New results for an entrainment coefficient that varies linearly with 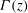 $\varGamma (z)$ and thus captures experimental values far more realistically are presented for forced plumes.
$\varGamma (z)$ and thus captures experimental values far more realistically are presented for forced plumes.