Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T14:54:38.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-dimensional energy spectra in high-Reynolds-number turbulent boundary layers

Published online by Cambridge University Press:  02 August 2017

Dileep Chandran Open the ORCID record for Dileep Chandran [Opens in a new window] ,
Rio Baidya ,
Jason P. Monty  and
Ivan Marusic
Dileep Chandran*
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Rio Baidya
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Jason P. Monty
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Here, we report the measurements of two-dimensional (2-D) spectra of the streamwise velocity ($u$) in a high-Reynolds-number turbulent boundary layer. A novel experiment employing multiple hot-wire probes was carried out at friction Reynolds numbers ranging from 2400 to 26 000. Taylor’s frozen turbulence hypothesis is used to convert temporal-spanwise information into a 2-D spatial spectrum which shows the contribution of streamwise (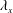$\unicode[STIX]{x1D706}_{x}$) and spanwise (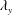$\unicode[STIX]{x1D706}_{y}$) length scales to the streamwise variance at a given wall height ($z$). At low Reynolds numbers, the shape of the 2-D spectra at a constant energy level shows 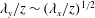$\unicode[STIX]{x1D706}_{y}/z\sim (\unicode[STIX]{x1D706}_{x}/z)^{1/2}$ behaviour at larger scales, which is in agreement with the existing literature at a matched Reynolds number obtained from direct numerical simulations. However, at high Reynolds numbers, it is observed that the square-root relationship tends towards a linear relationship (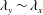$\unicode[STIX]{x1D706}_{y}\sim \unicode[STIX]{x1D706}_{x}$), as required for self-similarity and predicted by the attached eddy hypothesis.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , R1
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Baars, W. J., Squire, D. T., Talluru, K. M., Abbassi, M. R., Hutchins, N. & Marusic, I. 2016 Wall-drag measurements of smooth- and rough-wall turbulent boundary layers using a floating element. Exp. Fluids 57, 1–16.CrossRefGoogle Scholar
Baidya, R., Philip, J., Hutchins, N., Monty, J. P. & Marusic, I. 2017 Distance-from-the-wall scaling of turbulent motions in wall-bounded flows. Phys. Fluids 29 (2), 020712.CrossRefGoogle Scholar
Chandran, D., Baidya, R., Monty, J. P. & Marusic, I. 2016 Measurement of two-dimensional energy spectra in a turbulent boundary layer. In Proceedings of the 20th Australasian Fluid Mechanics Conference, Perth, Australia.Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 021404.Google Scholar
Chung, D., Marusic, I., Monty, J. P., Vallikivi, M. & Smits, A. J. 2015 On the universality of inertial energy in the log layer of turbulent boundary layer and pipe flows. Exp. Fluids 56, 1–10.Google Scholar
Davidson, P. A., Nickels, T. B. & Krogstad, P. Å. 2006 The logarithmic structure function law in wall-layer turbulence. J. Fluid Mech. 550, 51–60.CrossRefGoogle Scholar
Dennis, D. J. C. & Nickels, T. B. 2008 On the limitations of Taylor’s hypothesis in constructing long structures in a turbulent boundary layer. J. Fluid Mech. 614, 197–206.CrossRefGoogle Scholar
Hunt, J. C. R. & Morrison, J. F. 2000 Eddy structure in turbulent boundary layers. Eur. J. Mech. (B/Fluids) 19, 673–694.CrossRefGoogle Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Klewicki, J., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Monty, J. P. & Chong, M. S. 2009 Turbulent channel flow: comparison of streamwise velocity data from experiments and direct numerical simulation. J. Fluid Mech. 633, 461–474.CrossRefGoogle Scholar
Monty, J. P., Harun, Z. & Marusic, I. 2011 A parametric study of adverse pressure gradient turbulent boundary layers. Intl J. Heat Fluid Flow 32, 575–585.CrossRefGoogle Scholar
Morrison, W. R. B. & Kronauer, R. E. 1969 Structural similarity for fully developed turbulence in smooth tubes. J. Fluid Mech. 39, 117–141.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the k 1 -1 law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95, 074501.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Rosenberg, B. J., Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Turbulence spectra in smooth- and rough-wall pipe flow at extreme Reynolds numbers. J. Fluid Mech. 731, 46–63.CrossRefGoogle Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2014 Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 26, 105109.Google Scholar
de Silva, C. M., Squire, D. T., Hutchins, N. & Marusic, I. 2015 Towards capturing large scale coherent structures in boundary layers using particle image velocimetry. In Proceedings of the 7th Australian Conference on Laser Diagnostics in Fluid Mechanics and Combustion, Melbourne, Australia.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2005 Energetic spanwise modes in the logarithmic layer of a turbulent boundary layer. J. Fluid Mech. 545, 141–162.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar