Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T03:35:50.627Z Has data issue: false hasContentIssue false
  • English
  • Français

Two tandem cylinders of different diameters in cross-flow: effect of an upstream cylinder on wake dynamics

Published online by Cambridge University Press:  11 December 2017

Longjun Wang ,
Md. Mahbub Alam Open the ORCID record for Md. Mahbub Alam [Opens in a new window]  and
Yu Zhou
Longjun Wang
Affiliation:
Institute for Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, China Digital Engineering Laboratory of Offshore Equipment, Shenzhen, China
Md. Mahbub Alam*
Affiliation:
Institute for Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, China Digital Engineering Laboratory of Offshore Equipment, Shenzhen, China
Yu Zhou
Affiliation:
Institute for Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, China Digital Engineering Laboratory of Offshore Equipment, Shenzhen, China
*
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This work aims to provide a systematic experimental study on the wake of two tandem cylinders of unequal diameters. The fluid dynamics around a circular cylinder of diameter 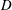$D$ placed in the wake of another circular cylinder with a smaller diameter of 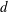$d$ is investigated, including the time-mean drag coefficient (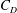$C_{D}$), the fluctuating drag and lift coefficients (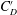$C_{D}^{\prime }$ and 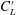$C_{L}^{\prime }$), the Strouhal number (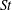$St$) and the flow structures. The Reynolds number based on 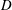$D$ is kept constant at 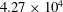$4.27\times 10^{4}$. The ratios 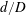$d/D$ and 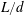$L/d$ vary from 0.2 to 1.0 and 1.0 to 8.0 respectively, where 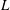$L$ is the distance from the upstream cylinder centre to the forward stagnation point of the downstream cylinder. The ratios 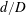$d/D$ and 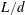$L/d$ are found, based on extensive hotwire, particle imaging velocimetry, pressure and flow visualization measurements, to have a marked influence on the wake dynamics behind the cylinders. As such, the flow is classified into the reattachment and co-shedding flow regimes, the latter being further subdivided into the lock-in, subharmonic lock-in and no lock-in regions. It is found that the critical spacing that divides the two regimes is dictated by the upstream-cylinder vortex formation length and becomes larger for smaller 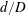$d/D$. The characteristic flow properties are documented in each regime and subdivided region, including the flow structure, 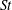$St$, wake width, vortex formation length and the lateral width between the two gap shear layers. The variations in 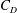$C_{D}$, 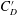$C_{D}^{\prime }$, 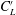$C_{L}^{\prime }$ and the pressure distribution around the downstream cylinder are connected to the flow physics.

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 836 , 10 February 2018 , pp. 5 - 42
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. M. 2014 The aerodynamics of a cylinder submerged in the wake of another. J. Fluids Struct. 51, 393–400.CrossRefGoogle Scholar
Alam, M. M. 2016 Lift forces induced by the phase lag between the vortex sheddings from two tandem bluff bodies. J. Fluids Struct. 65, 217–237.Google Scholar
Alam, M. M., Moriya, M., Takai, K. & Sakamoto, H. 2003 Fluctuating fluid forces acting on two circular cylinders in a tandem arrangement at a subcritical Reynolds number. J. Wind Engng Ind. Aerodyn. 91, 139–154.CrossRefGoogle Scholar
Alam, M. M. & Sakamoto, H. 2005 Investigation of Strouhal frequencies of two staggered bluff bodies and detection of multistable flow by wavelets. J. Fluids Struct. 20, 425–449.CrossRefGoogle Scholar
Alam, M. M., Sakamoto, H. & Zhou, Y. 2005 Determination of flow configurations and fluid forces acting on two staggered circular cylinders of equal diameter in cross-flow. J. Fluids Struct. 21, 363–394.CrossRefGoogle Scholar
Alam, M. M., Sakamoto, H. & Zhou, Y. 2006 Effect of a T-shaped plate on reduction in fluid forces acting on two tandem circular cylinders in a cross-flow. J. Wind Engng Ind. Aerodyn. 94, 525–551.Google Scholar
Alam, M. M. & Zhou, Y. 2007a Phase lag between vortex sheddings from two tandem bluff bodies. J. Fluids Struct. 23, 339–347.CrossRefGoogle Scholar
Alam, M. M. & Zhou, Y. 2007b Turbulent wake of an inclined cylinder with water running. J. Fluid Mech. 589, 261–303.CrossRefGoogle Scholar
Alam, M. M. & Zhou, Y. 2008 Strouhal numbers, forces and flow structures around two tandem cylinders of different diameters. J. Fluids Struct. 24, 505–524.Google Scholar
Alam, M. M., Zhou, Y. & Wang, X. W. 2011 The wake of two side-by-side square cylinders. J. Fluid Mech. 669, 432–471.Google Scholar
Arie, M., Kiya, M., Moriya, M. & Mori, H. 1983 Pressure fluctuations on the surface at two circular cylinders in tandem arrangement. Trans. ASME J. Fluids Engng 105, 161–166.CrossRefGoogle Scholar
Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.Google Scholar
Bloor, M. S. 1964 The transition to turbulence in the wake of a circular cylinder. J. Fluid Mech. 19, 290–304.CrossRefGoogle Scholar
Bokaian, A. & Geoola, F. 1984a Wake-induced galloping of two interfering circular cylinders. J. Fluid Mech. 146, 383–415.Google Scholar
Bokaian, A. & Geoola, F. 1984b Proximity-induced galloping of two interfering circular cylinders. J. Fluid Mech. 146, 417–449.Google Scholar
Borazjani, I. & Sotiropoulos, F. 2009 Vortex-induced vibrations of two cylinders in tandem arrangement in the proximity-wake interference region. J. Fluid Mech. 621, 321–364.CrossRefGoogle ScholarPubMed
Chyu, C.-K. & Rockwell, D. 1996 Near-wake structure of an oscillating cylinder: effect of controlled Kelvin–Helmholtz vortices. J. Fluid Mech. 322, 21–49.CrossRefGoogle Scholar
Gerrard, J. H. 1966 The mechanics of the formation region of vortices behind bluff bodies. J. Fluid Mech. 25, 401–413.Google Scholar
Gerrard, J. H. 1978 The wakes of cylindrical bluff bodies at low Reynolds number. Proc. R. Soc. Lond. A 288, 351–382.Google Scholar
Griffin, O. M. & Ramberg, S. E. 1974 The vortex street wakes of vibrating cylinders. J. Fluid Mech. 66, 553–576.Google Scholar
Gursul, I. & Rockwell, D. 1990 Vortex street impinging upon an elliptical leading edge. J. Fluid Mech. 211, 211–242.Google Scholar
Huang, S. & Sworn, A. 2011 Some observations of two interfering VIV circular cylinders of unequal diameters in tandem. J. Hydrodyn. 23, 535–543.CrossRefGoogle Scholar
Igarashi, T. 1981 Characteristics of the flow around two circular cylinders arranged in tandem, 1st report. Bull. JSME 24, 323–331.Google Scholar
Igarashi, T. 1982 Characteristics of a flow around two circular cylinders of different diameters arranged in tandem. Bull. JSME 25, 349–357.Google Scholar
Igarashi, T. 1984 Characteristics of the flow around two circular cylinders arranged in tandem, 2nd report. Bull. JSME 27, 2380–2387.CrossRefGoogle Scholar
Jendrzejcyk, J. A. & Chen, S. S. 1986 Fluid forces on two circular cylinders in crossflow. In Proceedings of the Flow-Induced Vibration, vol. 104, pp. 1–13. ASME, PVP.Google Scholar
Khabbouchi, I., Fellouah, H., Ferchichi, M. & Guellouz, M. S. 2014 Effects of free-stream turbulence and Reynolds number on the separated shear layer from a circular cylinder. J. Wind Engng Ind. Aerodyn. 135, 46–56.Google Scholar
Kim, S., Alam, M. M. & Zhou, Y. 2009 Flow-induced vibrations of two circular cylinders in tandem arrangement. Part 1. Characteristics of vibration. J. Wind Engng Ind. Aerodyn. 97, 304–311.Google Scholar
Kiya, M., Arie, M., Tamura, H. & Mori, H. 1980 Vortex shedding from two circulars in staggered arrangement. J. Fluids Engng 102, 166–173.Google Scholar
Laneville, A., Gartshore, I. S. & Parkinson, G. V. 1975 An explanation of some effects of turbulence on bluff bodies. In Proceedings of the Fourth International Conference on Wind Effects on Buildings & Structure, Heathrow, UK, K75–363 (ed. Eator, K. J.), pp. 333–341. Cambridge University Press.Google Scholar
Lee, D. J. & Smith, C. A. 1991 Effect of vortex core distortion on blade–vortex interaction. AIAA J. 29, 1355–1363.Google Scholar
Lee, S. J., Lee, S. I. & Park, C. W. 2004 Reducing the drag on a circular cylinder by upstream installation of a small control rod. Fluid Dyn. Res. 34, 233–250.Google Scholar
Lin, J. C., Yang, Y. & Rockwell, D. 2002 Flow past two cylinders in tandem: instantaneous and averaged flow structure. Trans. ASME J. Fluids Struct. 16, 1059–1071.CrossRefGoogle Scholar
Ljungkrona, L., Norberg, C. & Sunden, B. 1991 Free-stream turbulence and tube spacing effects on surface pressure fluctuations for two tubes in an in-line arrangement. J. Fluids Struct. 5, 701–727.Google Scholar
Ljungkrona, L. & Sunden, B. 1993 Flow visualization and surface pressure measurement on two tubes in an inline arrangement. Exp. Therm. Fluid Sci. 6, 15–27.CrossRefGoogle Scholar
Mahir, N. & Rockwell, D. 1996 Vortex formation from a forced system of two cylinders. Part 1. Tandem arrangement. J. Fluid Mech. 10, 473–489.CrossRefGoogle Scholar
Nakaguchi, H., Hashimoto, K. & Muto, S. 1968 An experimental study on aerodynamic drag of rectangular cylinder. J. Japan. Soc. Aeronaut. Space Sci. 16, 1–5.Google Scholar
Nakamura, H. & Igarashi, T. 2004 Variation of Nusselt number with flow regimes behind a circular cylinder for Reynolds numbers from 70 to 30 000. Intl J. Heat Mass Transfer 47, 5169–5173.CrossRefGoogle Scholar
Nakamura, Y. & Ohya, Y. 1984 The effects of turbulence on the mean flow past two-dimensional rectangular cylinders. J. Fluid Mech. 149, 255–273.CrossRefGoogle Scholar
Novak, J. 1974 Strouhal number of a square prism, angle iron and two circular cylinders arranged in tandem. Acta. Tech. Czech. Acad. Sci. 3, 361–373.Google Scholar
Ohya, Y., Okajima, A. & Hayashi, M. 1989 Wake interference and vortex shedding. In Encyclopedia of Fluid Mechanics (ed. Cheremisinoff, N. P.), pp. 323–389. Gulf.Google Scholar
Peltzer, R. D. & Rooney, D. M. 1985 Near wake properties of a strumming marine cable: an experimental study. Trans. ASME J. Fluids Engng 107, 86–91.CrossRefGoogle Scholar
Rockwell, D. 1998 Vortex–body interactions. Annu. Rev. Fluid Mech. 30, 199–229.Google Scholar
Roshko, A. 1955 On the wake and drag of bluff bodies. J. Aeronaut. Sci. 22, 124–132.CrossRefGoogle Scholar
Roshko, A. 1993 Perspectives on bluff body aerodynamics. J. Wind Engng Ind. Aerodyn. 49, 79–100.Google Scholar
Saha, A. K. 2007 Far-wake characteristics of two-dimensional flow past a normal flat plate. Phys. Fluids 19, 128110.Google Scholar
Sakamoto, H. & Haniu, H. 1988 Aerodynamic forces acting on two square prisms placed vertically in a turbulent boundary layer. J. Wind Engng Ind. Aerodyn. 31, 41–66.Google Scholar
So, R. M. C. & Savkar, S. D. 1981 Buffeting forces on rigid circular cylinders in cross flows. J. Fluid Mech. 105, 397–425.Google Scholar
Sumner, D. 2010 Two circular cylinders in cross-flow: a review. J. Fluids Struct. 26, 849–899.CrossRefGoogle Scholar
Unal, U. O. & Atlar, M. 2010 An experimental investigation into the effect of vortex generators on the near-wake flow of a circular cylinder. Exp. Fluids 48, 1059–1079.Google Scholar
Xu, G. & Zhou, Y. 2004 Strouhal numbers in the wake of two inline cylinders. Exp. Fluids 37, 248–256.CrossRefGoogle Scholar
Yiu, M. W., Zhou, Y. & Zhu, Y. G. 2004 Passive scalar transport in a turbulent cylinder wake in the presence of a downstream cylinder. Flow Turbul. Combust. 72, 449–461.Google Scholar
Zdravkovich, M. M. 1977 Review of flow interference between two circular cylinders in various arrangements. Trans. ASME J. Fluids Engng 99, 618–633.CrossRefGoogle Scholar
Zdravkovich, M. M. 1987 The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1, 239–261.Google Scholar
Zdravkovich, M. M. 1988 Review of interference-induced oscillations in flow past two parallel circular cylinders in various arrangements. J. Wind Engng Ind. Aerodyn. 28, 183–200.Google Scholar
Zdravkovich, M. M. 1997 Flow Around Circular Cylinders: Fundamentals, vol. 1. Oxford Science Publications.Google Scholar
Zdravkovich, M. M. & Pridden, D. L. 1977 Interference between two circular cylinders: series of unexpected discontinuities. J. Wind Engng Ind. Aerodyn. 2, 255–270.Google Scholar
Zhang, H. & Melbourne, W. H. 1992 Interference between two circular cylinders in tandem in turbulent flow. J. Wind Engng Ind. Aerodyn. 41–44, 589–600.Google Scholar
Zhang, M. M., Cheng, L. & Zhou, Y. 2006 Closed-loop controlled vortex–airfoil interactions. Phys. Fluids 18, 046102.CrossRefGoogle Scholar
Zhao, M., Cheng, L., Teng, B. & Dong, G. 2007 Hydrodynamic forces on dual cylinders of different diameters in steady current. J. Fluids Struct. 23, 59–83.Google Scholar
Zhao, M., Cheng, L., Teng, B. & Liang, D. 2005 Numerical simulation of viscous flow past two circular cylinders of different diameters. Appl. Ocean Res. 27, 39–55.Google Scholar
Zhou, Y. & Alam, M. M. 2016 Wake of two interacting circular cylinders: a review. Intl J. Heat Mass Transfer 62, 510–537.Google Scholar
Zhou, Y., Du, C., Mi, J. & Wang, X. W. 2012 Turbulent round jet control using two steady mini-jets. AIAA J. 50, 736–740.Google Scholar
Zhou, Y. & Yiu, M. W. 2006 Flow structure, momentum and heat transport in a two-tandem-cylinder wake. J. Fluid Mech. 548, 17–48.Google Scholar