Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T15:26:50.888Z Has data issue: false hasContentIssue false
  • English
  • Français

The turbulent/non-turbulent interface in an inclined dense gravity current

Published online by Cambridge University Press:  20 January 2015

Dominik Krug ,
Markus Holzner ,
Beat Lüthi ,
Marc Wolf ,
Wolfgang Kinzelbach  and
Arkady Tsinober
Dominik Krug*
Affiliation:
Institute of Environmental Engineering, ETH Zurich, Zurich 8093, Switzerland
Markus Holzner
Affiliation:
Institute of Environmental Engineering, ETH Zurich, Zurich 8093, Switzerland
Beat Lüthi
Affiliation:
Institute of Environmental Engineering, ETH Zurich, Zurich 8093, Switzerland
Marc Wolf
Affiliation:
Institute of Environmental Engineering, ETH Zurich, Zurich 8093, Switzerland
Wolfgang Kinzelbach
Affiliation:
Institute of Environmental Engineering, ETH Zurich, Zurich 8093, Switzerland
Arkady Tsinober
Affiliation:
Faculty of Engineering, Tel Aviv University, Ramat Aviv, 69978, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an experimental investigation of entrainment and the dynamics near the turbulent/non-turbulent interface in a dense gravity current. The main goal of the study is to investigate changes in the interfacial physics due to the presence of stratification and to examine their impact on the entrainment rate. To this end, three-dimensional data sets of the density and the velocity fields are obtained through a combined scanning particle tracking velocimetry/laser-induced fluorescence approach for two different stratification levels with inflow Richardson numbers of 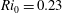$\mathit{Ri}_{0}=0.23$ and 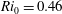$\mathit{Ri}_{0}=0.46$, respectively, at a Reynolds number around 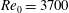$\mathit{Re}_{0}=3700$. An analysis conditioned on the instantaneous position of the turbulent/non-turbulent interface as defined by a threshold on enstrophy reveals an interfacial region that is in many aspects independent of the initial level of stratification. This is reflected most prominently in matching peaks of the gradient Richardson number 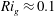$\mathit{Ri}_{g}\approx 0.1$ located approximately 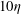$10{\it\eta}$ from the position of the interface inside the turbulent region, where 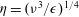${\it\eta}=({\it\nu}^{3}/{\it\epsilon})^{1/4}$ is the Kolmogorov scale, and ${\it\nu}$ and ${\it\epsilon}$ denote the kinematic viscosity and the rate of turbulent dissipation, respectively. A possible explanation for this finding is offered in terms of a cyclic evolution in the interaction of stratification and shear involving the buildup of density and velocity gradients through inviscid amplification and their subsequent depletion through molecular effects and pressure. In accordance with the close agreement of the interfacial properties for the two cases, no significant differences were found for the local entrainment velocity, 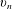$v_{n}$ (defined as the propagation velocity of an enstrophy isosurface relative to the fluid), at different initial stratification levels. Moreover, we find that the baroclinic torque does not contribute significantly to the local entrainment velocity. Comparing results for the surface area of the convoluted interface to estimates from fractal scaling theory, we identify differences in the interface geometry as the major factor in the reduction of the entrainment rate due to density stratification.

JFM classification

Geophysical and Geological Flows: Gravity currents Geophysical and Geological Flows: Stratified flows Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 765 , 25 February 2015 , pp. 303 - 324
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.Google Scholar
Cenedese, C. & Adduce, C. 2010 A new parameterization for entrainment in overflows. J. Phys. Oceanogr. 40 (8), 1835–1850.CrossRefGoogle Scholar
Chen, J., Odier, P., Rivera, M. & Ecke, R.2007. Laboratory measurement of entrainment and mixing in oceanic overflows. In ASME/JSME 2007 5th Joint Fluids Engineering Conference, San Diego, CA, FEDSM2007-37673, pp. 1283–1292. ASME.Google Scholar
Chevillard, L., Meneveau, C., Biferale, L. & Toschi, F. 2008 Modeling the pressure Hessian and viscous Laplacian in turbulence: comparisons with direct numerical simulation and implications on velocity gradient dynamics. Phys. Fluids 20 (10), 101504.Google Scholar
Corrsin, S. & Kistler, A.1954 The free-stream boundaries of turbulent flows. NACA Tech. Rep. TN-3133, TR-1244, pp. 1033–1064.Google Scholar
Ellison, T. H. & Turner, J. S. 1959 Turbulent entrainment in stratified flows. J. Fluid Mech. 6 (3), 423–448.Google Scholar
Holzner, M., Liberzon, A., Guala, M., Tsinober, A. & Kinzelbach, W. 2006 Generalized detection of a turbulent front generated by an oscillating grid. Exp. Fluids 41, 711–719.Google Scholar
Holzner, M., Liberzon, A., Nikitin, N., Lüthi, B., Kinzelbach, W. & Tsinober, A. 2008 A Lagrangian investigation of the small-scale features of turbulent entrainment through particle tracking and direct numerical simulation. J. Fluid Mech. 598, 465–475.Google Scholar
Holzner, M. & Lüthi, B. 2011 Laminar superlayer at the turbulence boundary. Phys. Rev. Lett. 106 (13), 134503.Google Scholar
Krug, D., Holzner, M., Lüthi, B., Wolf, M., Kinzelbach, W. & Tsinober, A. 2013 Experimental study of entrainment and interface dynamics in a gravity current. Exp. Fluids 54 (5), 1–13.Google Scholar
Krug, D., Holzner, M., Lüthi, B., Wolf, M., Tsinober, A. & Kinzelbach, W. 2014 A combined scanning PTV/LIF technique to simultaneously measure the full velocity gradient tensor and the 3D density field. Meas. Sci. Technol. 25 (6), 065301.Google Scholar
Legg, S., Briegleb, B., Chang, Y., Chassignet, E. P., Danabasoglu, G., Ezer, T., Gordon, A. L., Griffies, S., Hallberg, R., Jackson, L., Large, W., Özgökmen, T. M., Peters, H., Price, J., Riemenschneider, U., Wu, W., Xu, X. & Yang, J. 2009 Improving oceanic overflow representation in climate models: the Gravity Current Entrainment Climate Process Team. Bull. Am. Meteorol. Soc. 90, 657–670.Google Scholar
MacDonald, D. G., Carlson, J. & Goodman, L. 2013 On the heterogeneity of stratified-shear turbulence: observations from a near-field river plume. J. Geophys. Res. 118 (11), 6223–6237.Google Scholar
Mellado, J. P. 2010 The evaporatively driven cloud-top mixing layer. J. Fluid Mech. 660, 5–36.Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Odier, P., Chen, J. & Ecke, R. E. 2012 Understanding and modeling turbulent fluxes and entrainment in a gravity current. Physica D 241 (3), 260–268.Google Scholar
Odier, P., Chen, J. & Ecke, R. E. 2014 Entrainment and mixing in a laboratory model of oceanic overflow. J. Fluid Mech. 746, 498–535.CrossRefGoogle Scholar
Philip, J., Meneveau, C., de Silva, C. M. & Marusic, I. 2014 Multiscale analysis of fluxes at the turbulent/non-turbulent interface in high Reynolds number boundary layers. Phys. Fluids 26 (1), 015105.Google Scholar
Pollard, R. T., Rhines, P. B. & Thompson, R. 1972 The deepening of the wind-mixed layer. Geophys. Fluid Dyn. 4 (1), 381–404.Google Scholar
Rahmstorf, S. 2002 Ocean circulation and climate during the past 120 000 years. Nature 419 (6903), 207–214.Google Scholar
van Reeuwijk, M. & Holzner, M. 2014 The turbulence boundary of a temporal jet. J. Fluid Mech. 739, 254–275.Google Scholar
da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46, 567–590.Google Scholar
da Silva, C. B. T. & Rodrigo, R. 2010 The thickness of the turbulent/nonturbulent interface is equal to the radius of the large vorticity structures near the edge of the shear layer. Phys. Fluids 22 (12), 121702.Google Scholar
de Silva, C. M., Philip, J., Chauhan, K., Meneveau, C. & Marusic, I. 2013 Multiscale geometry and scaling of the turbulent–nonturbulent interface in high Reynolds number boundary layers. Phys. Rev. Lett. 111, 044501.Google Scholar
Sreenivasan, K. R., Ramshankar, R. & Meneveau, C. 1989 Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Proc. R. Soc. Lond. A 421 (1860), 79–108.Google Scholar
Taveira, R. R. & da Silva, C. B. 2014 Characteristics of the viscous superlayer in shear free turbulence and in planar turbulent jets. Phys. Fluids 26 (2), 021702.Google Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence, 2nd edn (An Informal Introduction to Turbulence) , Springer.Google Scholar
Wells, M., Cenedese, C. & Caulfield, C. P. 2010 The relationship between flux coefficient and entrainment ratio in density currents. J. Phys. Oceanogr. 40 (12), 2713–2727.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.Google Scholar
Wolf, M., Holzner, M., Lüthi, B., Krug, D., Kinzelbach, W. & Tsinober, A. 2013 Effects of mean shear on the local turbulent entrainment process. J. Fluid Mech. 731, 95–116.Google Scholar
Wolf, M., Lüthi, B., Holzner, M., Krug, D., Kinzelbach, W. & Tsinober, A. 2012 Investigations on the local entrainment velocity in a turbulent jet. Phys. Fluids 24 (10), 105110.CrossRefGoogle Scholar