Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-20T06:07:53.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent Schmidt number and eddy diffusivity change with a chemical reaction

Published online by Cambridge University Press:  30 July 2014

Tomoaki Watanabe ,
Yasuhiko Sakai ,
Kouji Nagata  and
Osamu Terashima
Tomoaki Watanabe*
Affiliation:
Department of Mechanical Science and Engineering, Nagoya University, Nagoya 464-8603, Japan
Yasuhiko Sakai
Affiliation:
Department of Mechanical Science and Engineering, Nagoya University, Nagoya 464-8603, Japan
Kouji Nagata
Affiliation:
Department of Mechanical Science and Engineering, Nagoya University, Nagoya 464-8603, Japan
Osamu Terashima
Affiliation:
Department of Mechanical Science and Engineering, Nagoya University, Nagoya 464-8603, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

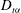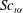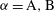We provide empirical evidence that the eddy diffusivity $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}D_{{t}\alpha }$ and the turbulent Schmidt number ${\mathit{Sc}}_{{t}\alpha }$ of species $\alpha $ ($\alpha =\mathrm{A}, \mathrm{B}$ or 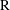$\mathrm{R}$) change with a second-order chemical reaction (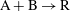$\mathrm{A} + \mathrm{B} \rightarrow \mathrm{R}$). In this study, concentrations of the reactive species and axial velocity are simultaneously measured in a planar liquid jet. Reactant A is premixed into the jet flow and reactant B is premixed into the ambient flow. An optical fibre probe based on light absorption spectrometry is combined with I-type hot-film anemometry to simultaneously measure concentration and velocity in the reactive flow. The eddy diffusivities and the turbulent Schmidt numbers are estimated from the simultaneous measurement results. The results show that the chemical reaction increases 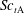${\mathit{Sc}}_{t\mathrm{A}}$; 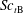${\mathit{Sc}}_{t\mathrm{B}}$ is negative in the region where the mean concentration of reactant B decreases in the downstream direction, and is positive in the non-reactive flow in the entire region on the jet centreline. It is also shown that 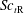${\mathit{Sc}}_{t\mathrm{R}}$ is positive in the upstream region whereas it is negative in the downstream region. The production terms of axial turbulent mass fluxes of reactant B and product R can produce axial turbulent mass fluxes opposite to the axial gradients of the mean concentrations. The changes in the production terms due to the chemical reaction result in the negative turbulent Schmidt number of these species. These results imply that the gradient diffusion model using a global constant turbulent Schmidt number poorly predicts turbulent mass fluxes in reactive flows.

JFM classification

Wakes/Jets: Jets Reacting Flows: Reacting Flows Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 754 , 10 September 2014 , pp. 98 - 121
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bilger, R. W., Saetran, L. R. & Krishnamoorthy, L. V. 1991 Reaction in a scalar mixing layer. J. Fluid Mech. 233, 211–242.Google Scholar
Bourne, J. R., Hilber, C. & Tovstiga, G. 1985 Kinetics of the azo coupling reactions between 1-naphthol and diazotised sulphanilic acid. Chem. Engng Commun. 37 (1–6), 293–314.Google Scholar
Bray, K. N. C., Libby, P. A., Masuya, G. & Moss, J. B. 1981 Turbulence production in premixed turbulent flames. Combust. Sci. Technol. 25, 127–140.Google Scholar
Brown, R. J. & Bilger, R. W. 1998a Experiments on a reacting plume-1. Conventional concentration statistics. Atmos. Environ. 32 (4), 611–628.CrossRefGoogle Scholar
Brown, R. J. & Bilger, R. W. 1998b Experiments on a reacting plume-2. Conditional concentration statistics. Atmos. Environ. 32 (4), 629–646.CrossRefGoogle Scholar
de Bruyn Kops, S. M., Riley, J. J. & Kosaly, G. 2001 Direct numerical simulation of reacting scalar mixing layers. Phys. Fluids 13, 1450–1465.Google Scholar
Chakraborty, N. & Cant, R. S. 2009 Effects of Lewis number on scalar transport in turbulent premixed flames. Phys. Fluids 21, 035110.Google Scholar
Cheng, R. K. & Shepherd, I. G. 1991 The influence of burner geometry on premixed turbulent flame propagation. Combust. Flame 85, 7–26.CrossRefGoogle Scholar
Chornyi, A. D. & Zhdanov, V. L. 2010 Verification of chemical reaction rate models in turbulent reacting flows at Schmidt number considerably exceeding 1. J. Engng Phys. Thermophys. 83 (3), 513–524.CrossRefGoogle Scholar
Combest, D. P., Ramachandran, P. A. & Dudukovic, M. 2011 On the gradient diffusion hypothesis and passive scalar transport in turbulent flows. Ind. Engng Chem. Res. 50 (15), 8817–8823.Google Scholar
Dutta, A. & Tarbell, J. M. 1989 Closure models for turbulent reacting flows. AIChE J. 35 (12), 2013–2027.Google Scholar
Fabregat, A., Pallarès, J., Cuesta, I. & Grau, F. X. 2010 Numerical simulations of a second-order chemical reaction in a plane turbulent channel flow. Intl J. Heat Fluid Flow 53, 4248–4263.Google Scholar
Feng, H., Olsen, M. G., Hill, J. C. & Fox, R. O. 2007 Simultaneous velocity and concentration field measurements of passive-scalar mixing in a confined rectangular jet. Exp. Fluids 42 (6), 847–862.Google Scholar
Feng, H., Olsen, M. G., Liu, Y., Fox, R. O. & Hill, J. C. 2005 Investigation of turbulent mixing in a confined planar-jet reactor. AIChE J. 51 (10), 2649–2664.Google Scholar
Flesch, T. K., Prueger, J. H. & Hatfield, J. L. 2002 Turbulent Schmidt number from a tracer experiment. Agric. Forest Meteorol. 111 (4), 299–307.Google Scholar
Fox, R. O. 2003 Computational Models for Turbulent Reacting Flows. Cambridge University Press.Google Scholar
Hanazaki, H. & Hunt, J. C. R. 1996 Linear processes in unsteady stably stratified turbulence. J. Fluid Mech. 318, 303–337.CrossRefGoogle Scholar
Hill, J. C. 1976 Homogeneous turbulent mixing with chemical reaction. Annu. Rev. Fluid Mech. 8, 135–161.CrossRefGoogle Scholar
Komori, S., Kanzaki, T. & Murakami, Y. 1994 Concentration correlation in a turbulent mixing layer with chemical reactions. J. Chem. Engng Japan 27 (6), 742–748.CrossRefGoogle Scholar
Komori, S. & Nagata, K. 1996 Effects of molecular diffusivities on counter-gradient scalar and momentum transfer in strongly stable stratification. J. Fluid Mech. 326, 205–237.Google Scholar
Komori, S., Nagata, K., Kanzaki, T. & Murakami, Y. 1993 Measurements of mass flux in a turbulent liquid flow with a chemical reaction. AIChE J. 39 (10), 1611–1620.Google Scholar
Libby, P. A. & Bray, K. N. C. 1981 Countergradient diffusion in premixed turbulent flames. AIAA J. 19 (2), 205–213.Google Scholar
Lignell, D. O., Chen, J. H. & Schmutz, H. A. 2011 Effects of Damköhler number on flame extinction and reignition in turbulent non-premixed flames using DNS. Combust. Flame 158 (5), 949–963.Google Scholar
Mell, W. E., Nilsen, V., Kosály, G. & Riley, J. J. 1994 Investigation of closure models for nonpremixed turbulent reacting flows. Phys. Fluids 6, 1331–1356.CrossRefGoogle Scholar
Mizobuchi, Y., Shinjo, J., Ogawa, S. & Takeno, T. 2005 A numerical study on the formation of diffusion flame islands in a turbulent hydrogen jet lifted flame. Proc. Combust. Inst. 30 (1), 611–619.Google Scholar
Nagata, K. & Komori, S. 2000 The effects of unstable stratification and mean shear on the chemical reaction in grid turbulence. J. Fluid Mech. 408, 39–52.Google Scholar
Nakamura, I., Sakai, Y. & Miyata, M. 1987 Diffusion of matter by a non-buoyant plume in grid-generated turbulence. J. Fluid Mech. 178, 379–403.Google Scholar
Nishiki, S., Hasegawa, T., Borghi, R. & Himeno, R. 2006 Modelling of turbulent scalar flux in turbulent premixed flames based on DNS databases. Combust. Theor. Model. 10 (1), 39–55.Google Scholar
Patterson, G. K. 1981 Application of turbulence fundamentals to reactor modelling and scaleup. Chem. Engng Commun. 8, 25–52.Google Scholar
Pitsch, H. 2006 Large-eddy simulation of turbulent combustion. Annu. Rev. Fluid Mech. 38, 453–482.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Sawford, B. L. 2006 Lagrangian stochastic modelling of chemical reaction in a scalar mixing layer. Boundary-Layer Meteorol. 118 (1), 1–23.Google Scholar
Shepherd, I. G., Moss, J. B. & Bray, K. N. C.1982 Turbulent transport in a confined premixed flame. Nineteenth Symp. (Intl) on Combustion, pp. 423–431. The Combustion Institute.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Tominaga, Y. & Stathopoulos, T. 2007 Turbulent Schmidt numbers for CFD analysis with various types of flowfield. Atmos. Environ. 41 (37), 8091–8099.Google Scholar
Toor, H. L. 1969 Turbulent mixing of two species with and without chemical reactions. Ind. Engng Chem. Fundam. 8 (4), 655–659.Google Scholar
Toor, H. L. 1993 Effect of chemical reactions on turbulent diffusivities. AIChE J. 39 (10), 1603–1610.Google Scholar
Veynante, D., Trouvé, A., Bray, K. N. C. & Mantel, T. 1997 Gradient and counter-gradient scalar transport in turbulent premixed flames. J. Fluid Mech. 332, 263–293.Google Scholar
Veynante, D. & Vervisch, L. 2002 Turbulent combustion modeling. Prog. Energy Combust. Sci. 28 (3), 193–266.Google Scholar
Wang, D. M. & Tarbell, J. M. 1993 Closure models for turbulent reacting flows with a nonhomogeneous concentration field. Chem. Engng Sci. 48 (23), 3907–3920.Google Scholar
Watanabe, T., Sakai, Y., Nagata, K. & Terashima, O. 2013 Joint statistics between velocity and reactive scalar in a turbulent liquid jet with a chemical reaction. Phys. Scr. T 155, 014039.Google Scholar
Watanabe, T., Sakai, Y., Nagata, K., Terashima, O. & Kubo, T. 2012 Simultaneous measurements of reactive scalar and velocity in a planar liquid jet with a second-order chemical reaction. Exp. Fluids 53 (5), 1369–1383.Google Scholar
Yimer, I., Campbell, I. & Jiang, L. Y. 2002 Estimation of the turbulent Schmidt number from experimental profiles of axial velocity and concentration for high-Reynolds-number jet flows. Can. Aeronaut. Space J. 48 (3), 195–200.Google Scholar