Turbulent hydraulic jumps in a stratified shear flow. Part 2

Abstract

Conditions are found in which stationary turbulent hydraulic jumps can occur in a shallow stably stratified shear flow of depth 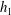$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}h_{1}$ moving over a rigid horizontal boundary at 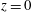$z =0$ and below a deep static layer of uniform density. The flow approaching a jump has uniform density and speed to a height 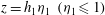$z = h_{1}\eta _{1}\ (\eta _{1} \le 1)$. Above this, in an interfacial layer 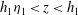$h_{1}\eta _{1}<z<h_{1}$, the density and speed decrease linearly to their values in a deep uniform and static layer above 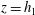$z = h_{1}$. The flow downstream of a jump is supposed to be similarly stratified to a height 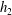$ h_{2}$, but with a lower layer of height 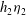$h_{2}\eta _{2}$. The flow approaching the jump is specified by 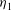$\eta _{1}$ and by a Froude number, Fr. Stationary jumps occur in the flow only if Fr is large enough to ensure that no internal waves can propagate upstream from the transition region. The flow downstream of the jump satisfies conditions of conservation of mass, volume and momentum fluxes, and closure is obtained by the selection of its gradient Richardson number, 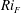${\mathit{Ri}}_{F}$. It is necessary that 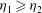$\eta _{1} \ge \eta _{2}$ for the entrainment of fluid into the moving layer from the overlying deep layer to be non-negative. The jump height, 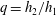$q = h_{2}/h_{1}$, always exceeds unity (i.e. jumps are, overall, of elevation) and the mean thickness of the flowing layer, 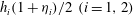$h_{i}(1+ \eta _{i})/2\ (i = 1, 2)$, increases through the jump. There are two types of jumps, one in which the thickness of the lower layer, $h_{i}\eta _{i}$, increases (and all isopycnals are raised by the transition) and a second in which 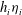$h_{i}\eta _{i}$ decreases even though 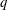$q$ and the mean thickness ratio, 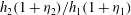$h_{2}(1+ \eta _{2})/ h_{1}(1 + \eta _{1})$, are greater than one. Two possible solutions for the downstream flow (i.e. 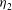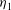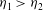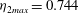two jumps of different heights, $q$, and different shape parameters, $\eta _{2}$) are possible in limited ranges of Fr depending on $\eta _{1}$ when $\eta _{1} > \eta _{2}$, $= \eta _{2max}$, where $\eta _{2max} =0.744$ when 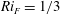${\mathit{Ri}}_{F} = 1/3$. Only single solutions are possible for upstream flows with 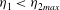$\eta _{1}< \eta _{2max}$. The two branches of the double solutions are distinguishable. For the ‘upper’ solutions, 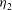$\eta _{2}$ increases as Fr increases, and all isopycnals are raised in the jump. The ‘lower’ of the double solutions are continuous with the single solutions (with 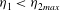$\eta _{1}<\eta _{2max}$), 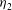$\eta _{2}$ decreases as Fr increases, and for most of the jumps the lower uniform layer decreases in thickness through the jump. For all solutions there is a reduction in the energy flux as fluid passes through a transition, and hence a loss of energy in the turbulent mixing of a jump, as required on physical grounds. The Osborn efficiency factor, 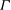$\varGamma $, is generally less than the canonical value of 0.2 for upper branch solutions but greater than 0.2 for the single and lower branch solutions. A loss in vorticity flux occurs in a turbulent jump. For a hydraulic jump to be possible when 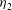$\eta _{2}$ is less than approximately 0.3, it is not generally necessary that the flow approaching a jump is unstable to Kelvin–Helmholtz (K–H) instability, but it is more common that upstream flows in which jumps can occur are dynamically unstable.