Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-25T07:38:04.745Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent diapycnal mixing in stratified shear flows: the influence of Prandtl number on mixing efficiency and transition at high Reynolds number

Published online by Cambridge University Press:  20 May 2015

H. Salehipour Open the ORCID record for H. Salehipour [Opens in a new window] ,
W. R. Peltier  and
A. Mashayek
H. Salehipour*
Affiliation:
Department of Physics, University of Toronto, Toronto, ON M5S 1A7, Canada
W. R. Peltier
Affiliation:
Department of Physics, University of Toronto, Toronto, ON M5S 1A7, Canada
A. Mashayek
Affiliation:
Department of Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA 02139-4307, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by the importance of small-scale turbulent diapycnal mixing to the closure of the large-scale meridional overturning circulation (MOC) of the oceans, we focus on a model problem which allows us to address the fundamental fluid mechanics that is expected to be characteristic of the oceanographic regime. Our model problem is one in which the initial conditions consist of a stably stratified parallel shear flow which evolves into the turbulent regime through the growth of a Kelvin–Helmholtz wave to finite amplitude followed by transition to turbulence. Through both linear stability analysis and direct numerical simulations (DNS), we investigate the secondary instabilities and the turbulent mixing at a fixed high Reynolds number and for a range of Prandtl numbers. We demonstrate that the oceanographically expected high value of the Prandtl number has a profound influence on the nature of the secondary instabilities that govern the transition process. Specifically through non-separable linear stability analysis, we discover new characteristics for the shear-aligned convective instability such that it is modified into a mixed mode that is driven both by static instability and by shear. The growth rate and ultimate strength of this mode are both strongly enhanced at higher 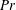$\mathit{Pr}$ while the growth rate and ultimate strength of the stagnation point instability (SPI), which may compete for control of the transition process, are simultaneously impeded. Of equal importance is the fact that, for higher 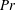$\mathit{Pr}$, the characteristic length scales associated with the dominant mixed mode of instability decrease and therefore there ceases to be a strong scale selectivity. In the limit of much higher 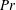$\mathit{Pr}$, we conjecture that a wide range of spatial scales become equally unstable so as to support an ‘ultraviolet catastrophe’, in which a direct injection of energy occurs into a broad range of scales simultaneously. We further establish the validity of these analytical results through a series of computationally challenging DNS analyses, and provide a detailed analysis of the efficiency of the turbulent mixing of the density field that occurs subsequent to transition and of the entrainment of fluid into the mixing layer from the high-speed flanks of the shear flow. We show that the mixing efficiency decreases monotonically with increase of the molecular value of the Prandtl number and the expansion of the shear layer is reduced as such entrainment diminishes.

JFM classification

Turbulent Flows: Stratified turbulence Waves/Free-surface Flows: Wave breaking
Type
Papers
Information
Journal of Fluid Mechanics , Volume 773 , 25 June 2015 , pp. 178 - 223
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5 (1), 113–133.Google Scholar
Browning, K. A. 1971 Structure of the atmosphere in the vicinity of large-amplitude Kelvin–Helmholtz billows. Q. J. R. Meteorol. Soc. 97, 283–299.Google Scholar
Brucker, K. A. & Sarkar, S. 2007 Evolution of an initially turbulent stratified shear layer. Phys. Fluids 19 (10), 105105.Google Scholar
Caulfield, C. P. & Peltier, W. R. 1994 Three-dimensionalization of the stratified mixing layer. Phys. Fluids 6, 3803–3805.Google Scholar
Caulfield, C. P. & Peltier, W. R. 2000 The anatomy of the mixing transition in homogeneous and stratified free shear layers. J. Fluid Mech. 413, 1–47.CrossRefGoogle Scholar
Corcos, G. & Sherman, F. 1976 Vorticity concentration and the dynamics of unstable free shear layers. J. Fluid Mech. 73, 241–264.Google Scholar
Deville, M. O., Fischer, P. F. & Mund, E. H. 2002 High-Order Methods for Incompressible Fluid Flow, vol. 9. Cambridge University Press.Google Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.Google Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2010 The Batchelor spectrum for mixing of passive scalars in isotropic turbulence. Flow Turbul. Combust. 85 (3–4), 549–566.CrossRefGoogle Scholar
Fischer, P. F. 1997 An overlapping Schwarz method for spectral element solution of the incompressible Navier–Stokes equations. J. Comput. Phys. 133 (1), 84–101.Google Scholar
Fischer, P. F., Kruse, G. W. & Loth, F. 2002 Spectral element methods for transitional flows in complex geometries. J. Sci. Comput. 17 (1–4), 81–98.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 Nek5000 web page.http://nek5000.mcs.anl.gov.Google Scholar
Fischer, P. F. & Mullen, J. 2001 Filter-based stabilization of spectral element methods. C. R. Acad. Sci. 332 (3), 265–270.Google Scholar
Garrett, C. & Kunze, E. 2007 Internal tide generation in the deep ocean. Annu. Rev. Fluid Mech. 39, 57–87.CrossRefGoogle Scholar
Geyer, W. R., Lavery, A. C., Scully, M. E. & Trowbridge, J. H. 2010 Mixing by shear instability at high Reynolds number. Geophys. Res. Lett. 37, L22607.CrossRefGoogle Scholar
Gotoh, T. & Yeung, P. K. 2013 Passive scalar transport in turbulence: a computational perspective. In Ten Chapters in Turbulence (ed. Kaneda, Y., Davidson, P. A. & Sreenivasan, K. R.). Cambridge University Press.Google Scholar
van Haren, H. & Gostiaux, L. 2010 A deep-ocean Kelvin–Helmholtz billow train. Geophys. Res. Lett. 37, L03605.Google Scholar
van Haren, H. & Gostiaux, L. 2012 Detailed internal wave mixing above a deep-ocean slope. J. Mar. Res. 70, 173–197.Google Scholar
van Haren, H., Gostiaux, L., Morozov, E. & Tarakanov, R. 2014 Extremely long Kelvin–Helmholtz billow trains in the Romanche Fracture Zone. Geophys. Res. Lett. 41, 8445–8451.CrossRefGoogle Scholar
Helmholtz, P. 1868 XLIII. On discontinuous movements of fluids. Phil. Mag. 36 (244), 337–346.Google Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10, 509–512.CrossRefGoogle Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 40, 169–184.Google Scholar
Kelvin, Lord 1871 Hydrokinetic solutions and observations. Phil. Mag. 10, 155–168.Google Scholar
Klaassen, G. P. & Peltier, W. R. 1985a The effect of Prandtl number on the evolution and stability of Kelvin–Helmholtz billows. Geophys. Astrophys. Fluid Dyn. 32, 23–60.Google Scholar
Klaassen, G. P. & Peltier, W. R. 1985b Evolution of finite amplitude Kelvin–Helmholtz billows in two spatial dimensions. J. Fluid Mech. 42, 1321–1339.Google Scholar
Klaassen, G. P. & Peltier, W. R. 1985c The onset of turbulence in finite amplitude Kelvin–Helmholtz billows. J. Fluid Mech. 155, 1–35.Google Scholar
Klaassen, G. P. & Peltier, W. R. 1991 The influence of stratification on secondary instabilities in free shear layers. J. Fluid Mech. 227, 71–106.Google Scholar
Kundu, P. & Cohen, I. 2008 Fluid Mechanics. Elsevier.Google Scholar
Legg, S., Ezer, T., Jackson, L., Briegleb, B. P., Danabasoglu, G., Large, W. G., Wu, W., Chang, Y., Özgökmen, T. M., Peters, H., Xu, X., Chassignet, E. P., Gordon, A. L., Griffies, S., Hallberg, R., Price, J., Riemenschneider, U. & Yang, J. 2009 Improving oceanic overflow representation in climate models: the gravity current entrainment climate process team. Bull. Am. Meteorol. Soc. 90, 657–670.Google Scholar
Linden, P. F. 1979 Mixing in stratified fluids. Geophys. Astrophys. Fluid Dyn. 13, 3–23.Google Scholar
Lorenz, E. N. 1955 Available potential energy and the maintenance of the general circulation. Tellus 7, 157–167.Google Scholar
Lozovatsky, I. D. & Fernando, H. J. S. 2012 Mixing efficiency in natural flows. Phil. Trans. R. Soc. Lond. A 371, 20120213.Google Scholar
Lumpkin, R. & Speer, K. 2007 Global ocean meridional overturning. J. Phys. Oceanogr. 37 (10), 2550–2562.Google Scholar
Maday, Y., Patera, A. T. & Rønquist, E. M. 1990 An operator-integration-factor splitting method for time-dependent problems: application to incompressible fluid flow. J. Sci. Comput. 5 (4), 263–292.Google Scholar
Marshall, J. & Speer, K. 2012 Closure of the meridional overturning circulation through southern ocean upwelling. Nat. Geosci. 5, 171–180.Google Scholar
Mashayek, A., Caulfield, C. P. & Peltier, W. R. 2013 Time-dependent, non-monotonic mixing in stratified turbulent shear flows: implications for oceanographic estimates of buoyancy flux. J. Fluid Mech. 736, 570–593.Google Scholar
Mashayek, A. & Peltier, W. R. 2011 Turbulence transition in stratified atmospheric and oceanic shear flows: Reynolds and Prandtl number controls upon the mechanism. Geophys. Res. Lett. 38, L16612,1–5.Google Scholar
Mashayek, A. & Peltier, W. R. 2012a The ‘zoo’ of secondary instabilities precursory to stratified shear flow transition. Part 1. Shear aligned convection, pairing, and braid instabilities. J. Fluid Mech. 708, 5–44.Google Scholar
Mashayek, A. & Peltier, W. R. 2012b The ‘zoo’ of secondary instabilities precursory to stratified shear flow transition. Part 2. The influence of stratification. J. Fluid Mech. 708, 45–70.Google Scholar
Mashayek, A. & Peltier, W. R. 2013 Shear induced mixing in geophysical flows: does the route to turbulence matter to its efficiency? J. Fluid Mech. 725, 216–261.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.Google Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30 (1), 539–578.Google Scholar
Moum, J. N., Nash, J. D. & Smyth, W. D. 2011 Narrowband oscillations in the upper equatorial ocean. Part 1. Interpretation as shear instabilities. J. Phys. Oceanogr. 41 (3), 397–411.Google Scholar
Munk, W. H. 1966 Abyssal recipes. Deep-Sea Res. 113, 207–230.Google Scholar
Munk, W. H. & Wunsch, C. 1998 Abyssal recipes. Part 2. Energetics of tidal and wind mixing. Deep-Sea Res. 45, 1977–2010.Google Scholar
Osborn, T. R. 1980 Estimates of the local rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10, 83–89.Google Scholar
Özgökmen, T. M., Fischer, P. F., Duan, J. & Iliescu, T. 2004a Entrainment in bottom gravity currents over complex topography from three-dimensional nonhydrostatic simulations. Geophys. Res. Lett. 31 (13), L13212.Google Scholar
Özgökmen, T. M., Fischer, P. F., Duan, J. & Iliescu, T. 2004b Three-dimensional turbulent bottom density currents from a high-order nonhydrostatic spectral element model. J. Phys. Oceanogr. 34 (9), 2006–2026.Google Scholar
Özgökmen, T. M., Iliescu, T. & Fischer, P. F. 2009 Large eddy simulation of stratified mixing in a three-dimensional lock-exchange system. Ocean Model. 26 (3), 134–155.Google Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.Google Scholar
Riley, J. J. & de Bruyn Kops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15, 2047–2059.Google Scholar
Salehipour, H., Stuhne, G. R. & Peltier, W. R. 2013 A higher order discontinuous Galerkin, global shallow water model: global ocean tides and aquaplanet benchmarks. Ocean Model. 69, 93–107.Google Scholar
Smyth, W. D. 2003 Secondary Kelvin–Helmholtz instability in weakly stratified shear flow. J. Fluid Mech. 497, 67–98.Google Scholar
Smyth, W. D. & Moum, J. N. 2000a Anisotropy of turbulence in stably stratified mixing layers. Phys. Fluids 12 (6), 1343–1362.Google Scholar
Smyth, W. D. & Moum, J. N. 2000b Length scales of turbulence in stably stratified mixing layers. Phys. Fluids 12, 1327.CrossRefGoogle Scholar
Smyth, W. D. & Moum, J. N. 2012 Ocean mixing by Kelvin–Helmholtz instability. Oceanography 25, 140–149.Google Scholar
Smyth, W. D., Moum, J. & Caldwell, D. 2001 The efficiency of mixing in turbulent patches: inferences from direct simulations and microstructure observations. J. Phys. Oceanogr. 31, 1969–1992.2.0.CO;2>CrossRefGoogle Scholar
Smyth, W. D. & Peltier, W. R. 1991 Instability and transition in finite amplitude Kelvin–Helmholtz and Holmboe waves. J. Fluid Mech. 228, 387–415.Google Scholar
Stillinger, D. C., Helland, K. N. & van Atta, C. W. 1983 Experiments on the transition of homogeneous turbulence to internal waves in a stratified fluid. J. Fluid Mech. 131, 91–122.Google Scholar
Strang, E. J. & Fernando, H. J. S. 2001 Entrainment and mixing in stratified shear flows. J. Fluid Mech. 428, 349–386.Google Scholar
Talley, L. D. 2013 Closure of the global overturning circulation through the Indian, Pacific, and Southern Oceans: schematics and transports. Oceanography 26 (1), 80–97.Google Scholar
Thorpe, S. A. 2005 The Turbulent Ocean. Cambridge University Press.Google Scholar
Tseng, Y. & Ferziger, J. H. 2001 Mixing and available potential energy in stratified flows. Phys. Fluids 13, 1281–1293.Google Scholar
Tufo, H. M. & Fischer, P. F. 2001 Fast parallel direct solvers for coarse grid problems. J. Parallel Distrib. Comput. 61 (2), 151–177.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar
Yeung, P. K., Donzis, D. A. & Sreenivasan, K. R. 2005 High-Reynolds-number simulation of turbulent mixing. Phys. Fluids 17 (8), 081703.Google Scholar
Supplementary material: File

Salehipour supplementary material

Salehipour supplementary material 1

Download Salehipour supplementary material(File)
File 219.4 KB