Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chouippe, Agathe
and
Uhlmann, Markus
2015.
Forcing homogeneous turbulence in direct numerical simulation of particulate flow with interface resolution and gravity.
Physics of Fluids,
Vol. 27,
Issue. 12,
Prosperetti, Andrea
2015.
Life and death by boundary conditions.
Journal of Fluid Mechanics,
Vol. 768,
Issue. ,
p.
1.
Dodd, Michael S.
and
Ferrante, Antonino
2016.
On the interaction of Taylor length scale size droplets and isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 806,
Issue. ,
p.
356.
M. Kuerten, J. G.
2016.
Point-Particle DNS and LES of Particle-Laden Turbulent flow - a state-of-the-art review.
Flow, Turbulence and Combustion,
Vol. 97,
Issue. 3,
p.
689.
Lashgari, Iman
Picano, Francesco
Breugem, Wim Paul
and
Brandt, Luca
2016.
Channel flow of rigid sphere suspensions: Particle dynamics in the inertial regime.
International Journal of Multiphase Flow,
Vol. 78,
Issue. ,
p.
12.
Saliakellis, Panagiotis
and
Yiantsios, Stergios G.
2016.
Macroscopic characteristics of heavy particle resuspension obtained from direct numerical simulations of pressure driven channel flow.
International Journal of Multiphase Flow,
Vol. 84,
Issue. ,
p.
188.
Fornari, Walter
Brandt, Luca
Chaudhuri, Pinaki
Lopez, Cyan Umbert
Mitra, Dhrubaditya
and
Picano, Francesco
2016.
Rheology of Confined Non-Brownian Suspensions.
Physical Review Letters,
Vol. 116,
Issue. 1,
De Marchis, M.
and
Milici, B.
2016.
Turbulence modulation by micro-particles in smooth and rough channels.
Physics of Fluids,
Vol. 28,
Issue. 11,
Costa, Pedro
Picano, Francesco
Brandt, Luca
and
Breugem, Wim-Paul
2016.
Universal Scaling Laws for Dense Particle Suspensions in Turbulent Wall-Bounded Flows.
Physical Review Letters,
Vol. 117,
Issue. 13,
Finn, Justin R.
Li, Ming
and
Apte, Sourabh V.
2016.
Particle based modelling and simulation of natural sand dynamics in the wave bottom boundary layer.
Journal of Fluid Mechanics,
Vol. 796,
Issue. ,
p.
340.
Wang, Lian-Ping
Peng, Cheng
Guo, Zhaoli
and
Yu, Zhaosheng
2016.
Flow Modulation by Finite-Size Neutrally Buoyant Particles in a Turbulent Channel Flow.
Journal of Fluids Engineering,
Vol. 138,
Issue. 4,
Kartushinsky, A.
Tisler, S.
Oliveira, J.L.G.
and
van der Geld, C.W.M.
2016.
Eulerian-Eulerian modelling of particle-laden two-phase flow.
Powder Technology,
Vol. 301,
Issue. ,
p.
999.
Vreman, A. W.
2016.
Particle-resolved direct numerical simulation of homogeneous isotropic turbulence modified by small fixed spheres.
Journal of Fluid Mechanics,
Vol. 796,
Issue. ,
p.
40.
Brandt, Luca
Picano, Francesco
and
Breugem, Wim-Paul
2016.
Progress in Turbulence VI.
Vol. 165,
Issue. ,
p.
311.
Fornari, Walter
Picano, Francesco
and
Brandt, Luca
2016.
Sedimentation of finite-size spheres in quiescent and turbulent environments.
Journal of Fluid Mechanics,
Vol. 788,
Issue. ,
p.
640.
Fornari, Walter
Picano, Francesco
Sardina, Gaetano
and
Brandt, Luca
2016.
Reduced particle settling speed in turbulence.
Journal of Fluid Mechanics,
Vol. 808,
Issue. ,
p.
153.
Javed, A.
Djijdeli, K.
and
Xing, J. T.
2016.
A coupled meshfree-mesh-based solution scheme on hybrid grid for flow-induced vibrations.
Acta Mechanica,
Vol. 227,
Issue. 8,
p.
2245.
Sierakowski, Adam J.
and
Prosperetti, Andrea
2016.
Resolved-particle simulation by the Physalis method: Enhancements and new capabilities.
Journal of Computational Physics,
Vol. 309,
Issue. ,
p.
164.
Yu, W.
Vinkovic, I.
and
Buffat, M.
2016.
Finite-size particles in turbulent channel flow: quadrant analysis and acceleration statistics.
Journal of Turbulence,
Vol. 17,
Issue. 11,
p.
1048.
Loyseau, X.F.
and
Verdin, P.G.
2016.
Statistical model of transient particle dispersion and deposition in vertical pipes.
Journal of Aerosol Science,
Vol. 101,
Issue. ,
p.
43.
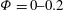 ${\it\Phi}=0{-}0.2$ with an immersed boundary method (IBM) used to account for the dispersed phase. The results show that the mean velocity profiles are significantly altered by the presence of a solid phase with a decrease of the von Kármán constant in the log-law. The overall drag is found to increase with the volume fraction, more than one would expect if just considering the increase of the system viscosity due to the presence of the particles. At the highest volume fraction investigated here,
${\it\Phi}=0{-}0.2$ with an immersed boundary method (IBM) used to account for the dispersed phase. The results show that the mean velocity profiles are significantly altered by the presence of a solid phase with a decrease of the von Kármán constant in the log-law. The overall drag is found to increase with the volume fraction, more than one would expect if just considering the increase of the system viscosity due to the presence of the particles. At the highest volume fraction investigated here, 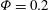 ${\it\Phi}=0.2$, the velocity fluctuation intensities and the Reynolds shear stress are found to decrease. The analysis of the mean momentum balance shows that the particle-induced stresses govern the dynamics at high
${\it\Phi}=0.2$, the velocity fluctuation intensities and the Reynolds shear stress are found to decrease. The analysis of the mean momentum balance shows that the particle-induced stresses govern the dynamics at high 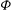 ${\it\Phi}$ and are the main responsible of the overall drag increase. In the dense limit, we therefore find a decrease of the turbulence activity and a growth of the particle induced stress, where the latter dominates for the Reynolds numbers considered here.
${\it\Phi}$ and are the main responsible of the overall drag increase. In the dense limit, we therefore find a decrease of the turbulence activity and a growth of the particle induced stress, where the latter dominates for the Reynolds numbers considered here.


