Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T06:53:44.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence statistics in Couette flow at high Reynolds number

Published online by Cambridge University Press:  08 October 2014

Sergio Pirozzoli ,
Matteo Bernardini  and
Paolo Orlandi
Sergio Pirozzoli*
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Università di Roma ‘La Sapienza’, Via Eudossiana 18, 00184 Rome, Italy
Matteo Bernardini
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Università di Roma ‘La Sapienza’, Via Eudossiana 18, 00184 Rome, Italy
Paolo Orlandi
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Università di Roma ‘La Sapienza’, Via Eudossiana 18, 00184 Rome, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

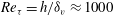We investigate the behaviour of the canonical turbulent Couette flow at computationally high Reynolds number through a series of large-scale direct numerical simulations. We achieve a Reynolds number $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}_{\tau } = h/\delta _v \approx 1000$, where 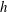$h$ is the channel half-height and 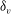$\delta _v$ is the viscous length scale at which some phenomena representative of the asymptotic Reynolds-number regime manifest themselves. While a logarithmic mean velocity profile is found to provide a reasonable fit of the data, including the skin friction, closer scrutiny shows that deviations from the log law are systematic, and probably increasing at higher Reynolds numbers. The Reynolds stress distribution shows the formation of a secondary outer peak in the streamwise velocity variance, which is associated with significant excess of turbulent production as compared to the local dissipation. This excess is related to the formation of large-scale streaks and rollers, which are responsible for a substantial fraction of the turbulent shear stress in the channel core, and for significant increase of the turbulence intermittency in the near-wall region.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 758 , 10 November 2014 , pp. 327 - 343
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Alfredsson, P. H., Örlü, R. & Segalini, A. 2012 A new formulation for the streamwise turbulence intensity distribution in wall-bounded turbulent flows. Eur. J. Mech. (B/Fluids) 36, 167–175.Google Scholar
Alfredsson, P. H., Segalini, A. & Örlü, R. 2011 A new scaling for the streamwise turbulence intensity in wall-bounded turbulent flows and what it tells us about the ‘outer’ peak. Phys. Fluids 23, 041702.Google Scholar
Avsarkisov, V., Hoyas, S., Oberlack, M. & García-Galache, J. P. 2014 Turbulent plane Couette flow at moderately high Reynolds number. J. Fluid Mech. 751, R1.CrossRefGoogle Scholar
Aydin, E. M. & Leutheusser, H. J. 1991 Plane-Couette flow between smooth and rough walls. Exp. Fluids 11, 302–312.Google Scholar
Bech, K. H., Tillmark, N., Alfredsson, P. H. & Andersson, H. I. 1995 An investigation of turbulent plane Couette flow at low Reynolds numbers. J. Fluid Mech. 286, 291–325.CrossRefGoogle Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to ${R}e_{\tau }=4000$ . J. Fluid Mech. 742, 171–191.Google Scholar
Bernardini, M., Pirozzoli, S., Quadrio, M. & Orlandi, P. 2013 Turbulent channel flow simulations in convecting reference frames. J. Comput. Phys. 232, 1–6.CrossRefGoogle Scholar
Busse, F. H. 1970 Bounds for turbulent shear flow. J. Fluid Mech. 41, 219–240.Google Scholar
El Telbany, M. M. M. & Reynolds, A. J. 1982 Velocity distributions in plane turbulent channel flows. Trans. ASME: J. Fluids Engng 104, 367–372.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulent structures. J. Fluid Mech. 287, 317–348.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of velocity fluctuations in turbulent channels up to ${R}e_{\tau } = 2003$ . Phys. Fluids 18, 011702.Google Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20, 101511.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108, 094501.Google Scholar
Hunt, J. C. R. & Morrison, J. F. 2001 Eddy structure in turbulent boundary layers. Eur. J. Mech. (B/Fluids) 19, 673–694.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hwang, Y. & Cossu, C. 2010 Amplification of coherent streaks in the turbulent Couette flow: an input–output analysis at low Reynolds number. J. Fluid Mech. 643, 333–348.Google Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11, 417–422.Google Scholar
Kitoh, O., Nakabayashi, K. & Nishimura, F. 2005 Experimental study on mean velocity and turbulence characteristics of plane Couette flow: low-Reynolds-number effects and large longitudinal vortical structure. J. Fluid Mech. 539, 199–227.CrossRefGoogle Scholar
Kitoh, O. & Umeki, M. 2008 Experimental study on large-scale streak structure in the core region of turbulent plane Couette flow. Phys. Fluids 20, 025107.Google Scholar
Komminaho, J., Lundbladh, A. & Johansson, A. V. 1996 Very large structures in plane turbulent Couette flow. J. Fluid Mech. 320, 259–285.Google Scholar
Lee, M. J. & Kim, J.1991 The structure of turbulence in a simulated plane Couette flow. In Proceedings of the 8th Symposium on Turbulent Shear Flows, Munich, pp. 5.3.1–5.3.6.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Metzger, M. M. & Klewicki, J. C. 2001 A comparative study of near-wall turbulence in high and low Reynolds number boundary layers. Phys. Fluids 13, 692–701.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Orlandi, P. 2000 Fluid Flow Phenomena: A Numerical Toolkit. Kluwer.Google Scholar
Papavassiliou, D. V. & Hanratty, T. J. 1997 Interpretation of large-scale structures observed in a turbulent planet Couette flow. Intl J. Heat Fluid Flow 18, 55–69.Google Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2011 Large-scale organization and inner–outer layer interactions in turbulent Couette–Poiseuille flows. J. Fluid Mech. 680, 534–563.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Reichardt, H. 1956 Über die Geschwindigkeitsverteilung in einer geradlinigen turbulenten Couetteströmung. Z. Angew. Math. Mech. 36, 26–29.CrossRefGoogle Scholar
Robertson, J. M.1959 On turbulent plane Couette flow. In Proceedings of the Sixth Midwestern Conference on Fluid Mechanics, University of Texas, Austin, pp. 169–182.Google Scholar
Schlatter, P. & Örlü, R. 2010 Quantifying the interaction between large and small scales in wall-bounded turbulent flows: a note of caution. Phys. Fluids 22, 051704.Google Scholar
Schlichting, H. & Gersten, K. 2000 Boundary Layer Theory, 8th edn. Springer.Google Scholar
Tillmark, N. & Alfredsson, P. H. 1992 Experiments on transition in plane Couette flow. J. Fluid Mech. 235, 89–102.CrossRefGoogle Scholar
Tillmark, N. & Alfredsson, P. H. 1998 Large scale structures in turbulent plane Couette flow. In Advances in Turbulence, VII (ed. Frisch, U.), Fluid Mechanics and Its Applications, vol. 46, pp. 59–62. Kluwer Academic.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Tsukahara, T., Kawamura, H. & Shingai, K. 2006 DNS of turbulent Couette flow with emphasis on the large-scale structure in the core region. J. Turbul. 7, 1–16.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.CrossRefGoogle Scholar