Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cheng, Zhen
Chauchat, Julien
Hsu, Tian-Jian
and
Calantoni, Joseph
2018.
Eddy interaction model for turbulent suspension in Reynolds-averaged Euler–Lagrange simulations of steady sheet flow.
Advances in Water Resources,
Vol. 111,
Issue. ,
p.
435.
Cheng, Zhen
Hsu, Tian-Jian
and
Chauchat, Julien
2018.
An Eulerian two-phase model for steady sheet flow using large-eddy simulation methodology.
Advances in Water Resources,
Vol. 111,
Issue. ,
p.
205.
Gonzalez-Ondina, Jose M.
Fraccarollo, Luigi
and
Liu, Philip L.-F.
2018.
Two-level, two-phase model for intense, turbulent sediment transport.
Journal of Fluid Mechanics,
Vol. 839,
Issue. ,
p.
198.
Thorne, Peter D.
Hurther, David
Cooke, Richard D.
Caceres, Ivan
Barraud, Pierre A.
and
Sánchez-Arcilla, Agustín
2018.
Developments in acoustics for studying wave-driven boundary layer flow and sediment dynamics over rippled sand-beds.
Continental Shelf Research,
Vol. 166,
Issue. ,
p.
119.
Fromant, G.
Mieras, R. S.
Revil‐Baudard, T.
Puleo, J. A.
Hurther, D.
and
Chauchat, J.
2018.
On Bedload and Suspended Load Measurement Performances in Sheet Flows Using Acoustic and Conductivity Profilers.
Journal of Geophysical Research: Earth Surface,
Vol. 123,
Issue. 10,
p.
2546.
Fromant, G.
Hurther, D.
van der Zanden, J.
van der A, D. A.
Cáceres, I.
O'Donoghue, T.
and
Ribberink, J. S.
2019.
Wave Boundary Layer Hydrodynamics and Sheet Flow Properties Under Large‐Scale Plunging‐Type Breaking Waves.
Journal of Geophysical Research: Oceans,
Vol. 124,
Issue. 1,
p.
75.
Zade, Sagar
Fornari, Walter
Lundell, Fredrik
and
Brandt, Luca
2019.
Buoyant finite-size particles in turbulent duct flow.
Physical Review Fluids,
Vol. 4,
Issue. 2,
Vergne, Adrien
Le Coz, Jérôme
Berni, Céline
and
Pierrefeu, Gilles
2020.
Using a Down‐Looking Multifrequency ABS for Measuring Suspended Sediments in Rivers.
Water Resources Research,
Vol. 56,
Issue. 2,
Akutina, Y.
Revil-Baudard, T.
Chauchat, J.
and
Eiff, O.
2020.
Experimental evidence of settling retardation in a turbulence column.
Physical Review Fluids,
Vol. 5,
Issue. 1,
Chen, Xiaohui
Zhang, Minxi
and
Yu, Guoliang
2020.
Depth-Averaged von Kármán Coefficient in Sediment-Laden Flows Using a Turbulent Kinetic Energy Balance.
Journal of Hydraulic Engineering,
Vol. 146,
Issue. 4,
Zheng, Xiaojing
Feng, Shengjun
and
Wang, Ping
2021.
Modulation of turbulence by saltating particles on erodible bed surface.
Journal of Fluid Mechanics,
Vol. 918,
Issue. ,
Naqshband, S.
Hurther, D.
Giri, S.
Bradley, R. W.
Kostaschuk, R. A.
Venditti, J. G.
and
Hoitink, A. J. F.
2021.
The Influence of Slipface Angle on Fluvial Dune Growth.
Journal of Geophysical Research: Earth Surface,
Vol. 126,
Issue. 4,
Wang, Ping
Wei, Qingqing
and
Zheng, Xiaojing
2021.
Differences of turbulence modulation by heavy particles on solid wall and erodible bed surface.
Physics of Fluids,
Vol. 33,
Issue. 11,
Zedel, Len
Hay, Alex E.
Wilson, Gregory W.
and
Hare, Jenna
2021.
Pulse Coherent Doppler Profiler Measurement of Bedload Transport.
Journal of Geophysical Research: Earth Surface,
Vol. 126,
Issue. 4,
Guta, Hélder
Hurther, David
and
Chauchat, Julien
2022.
Bedload and Concentration Effects on Turbulent Suspension Properties in Heavy Particle Sheet Flows.
Journal of Hydraulic Engineering,
Vol. 148,
Issue. 7,
Liu, Hongyou
Feng, Yuen
and
Zheng, Xiaojing
2022.
Experimental investigation of the effects of particle near-wall motions on turbulence statistics in particle-laden flows.
Journal of Fluid Mechanics,
Vol. 943,
Issue. ,
Rousseau, G.
and
Ancey, C.
2022.
An experimental investigation of turbulent free-surface flows over a steep permeable bed.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Chauchat, J.
Hurther, D.
Revil-Baudard, T.
Cheng, Z.
and
Hsu, T.-J.
2022.
Controversial turbulent Schmidt number value in particle-laden boundary layer flows.
Physical Review Fluids,
Vol. 7,
Issue. 1,
Guta, Hélder
Hurther, David
and
Chauchat, Julien
2024.
Turbulent kinetic energy budget of sediment-laden open-channel flows: bedload-induced wall-roughness similarity.
Journal of Fluid Mechanics,
Vol. 987,
Issue. ,
Feng, Yuen
Liu, Hongyou
and
Zheng, Xiaojing
2024.
The modulation of coherent structures by the near-wall motions of particles.
Journal of Fluid Mechanics,
Vol. 981,
Issue. ,
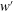 $w^{\prime }$) and streamwise (
$w^{\prime }$) and streamwise (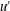 $u^{\prime }$) velocity fluctuations. This appears as an additional Reynolds shear stress in the near-wall region. It is also observed that the mobile sediment bed induces an increase of turbulence kinetic energy (TKE) across the boundary layer. However, the increased contribution of interaction events (
$u^{\prime }$) velocity fluctuations. This appears as an additional Reynolds shear stress in the near-wall region. It is also observed that the mobile sediment bed induces an increase of turbulence kinetic energy (TKE) across the boundary layer. However, the increased contribution of interaction events (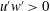 $u^{\prime }w^{\prime }>0$, i.e. quadrants I and III in the (
$u^{\prime }w^{\prime }>0$, i.e. quadrants I and III in the (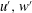 $u^{\prime },w^{\prime }$) plane) induces a decrease of the turbulent momentum diffusion and an increase of the turbulent concentration diffusion in the suspension region. This result provides an explanation for the modification of the von Kármán parameter and the turbulent Schmidt number observed in the literature for intense sediment transport.
$u^{\prime },w^{\prime }$) plane) induces a decrease of the turbulent momentum diffusion and an increase of the turbulent concentration diffusion in the suspension region. This result provides an explanation for the modification of the von Kármán parameter and the turbulent Schmidt number observed in the literature for intense sediment transport.


