Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T17:06:09.412Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence laws in natural bed flows

Published online by Cambridge University Press:  06 June 2016

Domenico Ferraro ,
Sergio Servidio ,
Vincenzo Carbone ,
Subhasish Dey  and
Roberto Gaudio
Domenico Ferraro*
Affiliation:
Dipartimento di Ingegneria Civile, Università della Calabria, 87036 Rende (CS), Italy
Sergio Servidio
Affiliation:
Dipartimento di Fisica, Università della Calabria, 87036 Rende (CS), Italy
Vincenzo Carbone
Affiliation:
Dipartimento di Fisica, Università della Calabria, 87036 Rende (CS), Italy
Subhasish Dey
Affiliation:
Department of Civil Engineering, Indian Institute of Technology Kharagpur, West Bengal 721302, India
Roberto Gaudio
Affiliation:
Dipartimento di Ingegneria Civile, Università della Calabria, 87036 Rende (CS), Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Characterization of turbulence in natural bed streams is one of the most fascinating problems of fluid dynamics. In this study, a statistical description of turbulence in a natural pebble bed flow is presented applying the laws of turbulence. A laboratory experiment was conducted to measure the three-dimensional instantaneous velocity components in a flow over heterogeneous coarse sediments that simulated a natural bed. 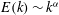The analysis reveals that the spectra (in Fourier space) show a power-law scaling, $E(k)\sim k^{{\it\alpha}}$, suggesting the presence of inertial range turbulence. The exponent ${\it\alpha}$ is slightly shallower than the Kolmogorov 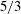$5/3$ scaling law, with this deviation possibly due to the bed roughness heterogeneity and to fluctuation anisotropy. The Taylor frozen-in approximation is broken at smaller scales towards the roughness crest level; therefore, a new statistical tool for the validation of this approximation is proposed. The Kolmogorov 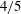$4/5$-law for the longitudinal increments and simultaneously the Monin–Yaglom 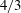$4/3$-law for the nonlinear normal fluxes (both in physical space) are preserved, providing an accurate estimation of the turbulent kinetic energy dissipation rate. The heterogeneity of the bed acts to induce the transport of finite kinetic helicity to the outer layer through persistently prolonged vortices. An associated 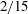$2/15$-law for the cascade of helicity has been locally found. These findings open a new direction in turbulence research for flows over highly rough beds.

JFM classification

Turbulent Flows: Shear layer turbulence Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 798 , 10 July 2016 , pp. 540 - 571
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aberle, J. 2007 Measurements of armour layer roughness geometry function and porosity. Acta Geophys. 55 (1), 23–32.CrossRefGoogle Scholar
Antohe, B. & Lage, J. 1997 A general two equation macroscopic turbulence model for incompressible flow in porous media. Intl J. Heat Mass Transfer 40 (13), 3013–3024.CrossRefGoogle Scholar
Antonia, R. A., Ould-Rouis, M., Anselmet, F. & Zhu, Y. 1997 Analogy between predictions of Kolmogorov and Yaglom. J. Fluid Mech. 332, 395–409.CrossRefGoogle Scholar
Betchov, R. 1961 Semi-isotropic turbulence and helicoidal flows. Phys. Fluids 4 (7), 925–926.CrossRefGoogle Scholar
Biferale, L., Musacchio, S. & Toschi, F. 2013 Split energy–helicity cascades in three-dimensional homogeneous and isotropic turbulence. J. Fluid Mech. 730, 309–327.CrossRefGoogle Scholar
Blackman, R. B. & Tukey, J. W. 1958 The measurement of power spectra from the point of view of communications engineering. Part I. Bell Sys. Tech. J. 37 (1), 185–282.CrossRefGoogle Scholar
Brissaud, A., Frisch, U., Leorat, J., Lesieur, M. & Mazure, A. 1973 Helicity cascades in fully developed isotropic turbulence. Phys. Fluids 16 (8), 1366–1367.CrossRefGoogle Scholar
Calaf, M., Hultmark, M., Oldroyd, H. J., Simeonov, V. & Parlange, M. B. 2013 Coherent structures and the k -1 spectral behaviour. Phys. Fluids 25 (12), 125107.CrossRefGoogle Scholar
Chen, Q., Chen, S. & Eyink, G. L. 2003 The joint cascade of energy and helicity in three-dimensional turbulence. Phys. Fluids 15 (2), 361–374.CrossRefGoogle Scholar
Chen, S. & Kraichnan, R. H. 1989 Sweeping decorrelation in isotropic turbulence. Phys. Fluids 1 (12), 2019–2024.CrossRefGoogle Scholar
Chkhetiani, O. G. 1996 On the third moments in helical turbulence. J. Expl Theor. Phys. Lett. 63 (10), 808–812.CrossRefGoogle Scholar
Cho, J. Y. N., Anderson, B. E., Barrick, J. D. W. & Thornhill, K. L. 2001 Aircraft observations of boundary layer turbulence- Intermittency and the cascade of energy and passive scalar variance. J. Geophys. Res. 106, 32469–32479.CrossRefGoogle Scholar
Del Alamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
Dey, S. 2014 Turbulence in open-channel flows. In Fluvial Hydrodynamics, pp. 95–187. Springer.CrossRefGoogle Scholar
Dey, S. & Das, R. 2012 Gravel-bed hydrodynamics: double-averaging approach. J. Hydraul. Engng ASCE 138 (8), 707–725.CrossRefGoogle Scholar
Dey, S., Das, R., Gaudio, R. & Bose, S. 2012 Turbulence in mobile-bed streams. Acta Geophys. 60 (6), 1547–1588.CrossRefGoogle Scholar
Dittrich, A. & Koll, K. 1997 Velocity field and resistance of flow over rough surface with large and small relative submergence. Intl J. Sedim. Res. 12 (3), 21–33.Google Scholar
Eidelman, A., Elperin, T., Gluzman, I. & Golbraikh, E. 2014 Helicity of mean and turbulent flow with coherent structures in Rayleigh-Bénard convective cell. Phys. Fluids 26 (6), 065103.CrossRefGoogle Scholar
Finnigan, J. 1985 Turbulent transport in flexible plant canopies. In The Forest-Atmosphere Interaction, pp. 443–480. Springer.CrossRefGoogle Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32 (1), 519–571.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence: The Legacy of AN Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Giménez-Curto, L. A. & Corniero, M. A. 2002 Flow characteristics in the interfacial shear layer between a fluid and a granular bed. J. Geophys. Res. 107 (C5), 12-1.Google Scholar
Giménez-Curto, L. A. & Lera, M. A. C. 1996 Oscillating turbulent flow over very rough surfaces. J. Geophys. Res. 101 (C9), 20745–20758.CrossRefGoogle Scholar
Gomez, T., Politano, H. & Pouquet, A. 2000 Exact relationship for third-order structure functions in helical flows. Phys. Rev. E 61 (5), 5321.CrossRefGoogle ScholarPubMed
Goring, D. G. & Nikora, V. I. 2002 Despiking acoustic doppler velocimeter data. J. Hydraul. Engng ASCE 128 (1), 117–126.CrossRefGoogle Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.CrossRefGoogle Scholar
Horiuti, K. & Ozawa, T. 2011 Multimode stretched spiral vortex and nonequilibrium energy spectrum in homogeneous shear flow turbulence. Phys. Fluids 23 (3), 035107.CrossRefGoogle Scholar
Katul, G. & Chu, C.-R. 1998 A theoretical and experimental investigation of energy-containing scales in the dynamic sublayer of boundary-layer flows. Boundary-Layer Meteorol. 86 (2), 279–312.CrossRefGoogle Scholar
Katul, G. G., Porporato, A. & Nikora, V. I. 2012 Existence of k -1 power-law scaling in the equilibrium regions of wall-bounded turbulence explained by Heisenberg’s eddy viscosity. Phys. Rev. E 86 (6), 066311.CrossRefGoogle ScholarPubMed
Keylock, C. J. 2015 Flow resistance in natural, turbulent channel flows: the need for a fluvial fluid mechanics. Water Resour. Res. 51, 4374–4390.CrossRefGoogle Scholar
Keylock, C. J., Nishimura, K., Nemoto, M. & Ito, Y. 2012 The flow structure in the wake of a fractal fence and the absence of an ‘inertial regime’. Environ. Fluid Mech. 12, 227–250.CrossRefGoogle Scholar
Keylock, C. J., Singh, A. & Foufoula-Georgiou, E. 2013 The influence of migrating bed forms on the velocity-intermittency structure of turbulent flow over a gravel bed. Geophys. Res. Lett. 40, 1351–1355.CrossRefGoogle Scholar
Kironoto, B. A. & Graf, W. H. 1994 Turbulence characteristics in rough uniform open-channel flow. Proc. Ice-Water Maritime Energy 106 (4), 333–344.CrossRefGoogle Scholar
Kolmogorov, A. 1941a The local structure of turbulence in incompressible viscous fluid for very large Reynolds’ numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Kolmogorov, A. N. 1941b Dissipation of energy in locally isotropic turbulence. Akad. Nauk SSSR Dokl. 32, 16.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13 (01), 82–85.CrossRefGoogle Scholar
Kraichnan, R. H. 1973 Helical turbulence and absolute equilibrium. J. Fluid Mech. 59 (04), 745–752.CrossRefGoogle Scholar
Kraichnan, R. H. & Panda, R. 1988 Depression of nonlinearity in decaying isotropic turbulence. Phys. Fluids 31 (9), 2395–2397.CrossRefGoogle Scholar
Kurien, S., Taylor, M. A. & Matsumoto, T. 2004 Isotropic third-order statistics in turbulence with helicity: the 2/15-law. J. Fluid Mech. 515, 87–97.CrossRefGoogle Scholar
de Lemos, M. J. S. 2012 Turbulence in Porous Media. Modeling and Applications. Elsevier.Google Scholar
de Lemos, M. & Pedras, M. 2001 Recent mathematical models for turbulent flow in saturated rigid porous media. Trans. ASME J. Fluids Engng 123, 935–940.CrossRefGoogle Scholar
Li, Y., Meneveau, C., Chen, S. & Eyink, G. L. 2006 Subgrid-scale modeling of helicity and energy dissipation in helical turbulence. Phys. Rev. E 74 (2), 026310.CrossRefGoogle ScholarPubMed
Lim, S.-Y. & Yang, S.-Q. 2006 Discussion of shear stress in smooth rectangular open-channel flows by Junke Guo and Pierre Y. Julien. J. Hydraul. Engng ASCE (6), 629–631.Google Scholar
Linkmann, M. F., Berera, A., McComb, W. D. & McKay, M. E. 2015 Nonuniversality and finite dissipation in decaying magnetohydrodynamic turbulence. Phys. Rev. Lett. 114 (23), 235001.CrossRefGoogle ScholarPubMed
L’vov, V. S., Podivilov, E. & Procaccia, I.1997 Exact result for the 3rd order correlations of velocity in turbulence with helicity, e-print arXiv:chao-dyn/9705016, p. 5016.Google Scholar
Manes, C., Poggi, D. & Ridolfi, L. 2011 Turbulent boundary layers over permeable walls: scaling and near-wall structure. J. Fluid Mech. 687, 141–170.CrossRefGoogle Scholar
Manes, C., Pokrajac, D. & McEwan, I. 2007 Double-averaged open-channel flows with small relative submergence. J. Hydraul. Engng 133 (8), 896–904.CrossRefGoogle Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22 (6), 065103.CrossRefGoogle Scholar
Matthaeus, W. H. & Goldstein, M. L. 1982 Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind. J. Geophys. Res. 87, 6011–6028.CrossRefGoogle Scholar
Matthes, G. H. 1947 Macroturbulence in natural stream flow. EOS Trans. AGU 28 (2), 255–265.Google Scholar
Mignot, E., Barthelemy, E. & Hurther, D. 2009 Double-averaging analysis and local flow characterization of near-bed turbulence in gravel-bed channel flows. J. Fluid Mech. 618, 279–303.CrossRefGoogle Scholar
Mininni, P. D. & Pouquet, A. 2009 Helicity cascades in rotating turbulence. Phys. Rev. E 79 (2), 026304.CrossRefGoogle ScholarPubMed
Moffatt, H. K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35 (01), 117–129.CrossRefGoogle Scholar
Monin, A. S. & Yaglom, A. M. 1971 Mechanics of turbulence. In Statistical Fluid Mechanics, MIT.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics: Mechanics of Turbulence, revised and enlarged edition. vol. 2. MIT.Google Scholar
Monin, A. S., Yaglom, A. M. & Lumley, J. L. 2007 Statistical Fluid Mechanics: Mechanics of Turbulence. vol. 1. Courier Corporation.Google Scholar
Nelkin, M. & Tabor, M. 1990 Time correlations and random sweeping in isotropic turbulence. Phys. Fluids A 2 (1), 81–83.CrossRefGoogle Scholar
Nezu, I. & Nakagawa, T. 1993 Turbulence in Open-Channel Flows, IAHR Monograph Series. Balkema.Google Scholar
Nikora, V. 2008 Hydrodynamics of gravel-bed rivers: scale issues. In Gravel-Bed Rivers VI: From Process Understanding to River Restoration. Elsevier.Google Scholar
Nikora, V. & Goring, D. 2000 Flow turbulence over fixed and weakly mobile gravel beds. J. Hydraul. Engng ASCE 126 (9), 679–690.CrossRefGoogle Scholar
Nikora, V., Goring, D., McEwan, I. & Griffiths, G. 2001 Spatially averaged open-channel flow over rough bed. J. Hydraul. Engng ASCE 127 (2), 123–133.CrossRefGoogle Scholar
Nikora, V., McEwan, I., McLean, S., Coleman, S., Pokrajac, D. & Walters, R. 2007 Double-averaging concept for rough-bed open-channel and overland flows: theoretical background. J. Hydraul. Engng 133 (8), 873–883.CrossRefGoogle Scholar
Nikora, V. I. & Smart, G. M. 1997 Turbulence characteristics of New Zealand gravel-bed rivers. J. Hydraul. Engng 123 (9), 764–773.CrossRefGoogle Scholar
Pedras, M. H. J. & de Lemos, M. J. S. 2001 Macroscopic turbulence modeling for incompressible flow through undeformable porous media. Intl J. Heat Mass Transfer 44 (6), 1081–1093.CrossRefGoogle Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Pinton, J. F. & Labbé, R. 1994 Correction to the Taylor hypothesis in swirling flows. J. Phys. II 4, 1461–1468.Google Scholar
Pokrajac, D., McEwan, I. & Nikora, V. 2008 Spatially averaged turbulent stress and its partitioning. Exp. Fluids 45 (1), 73–83.CrossRefGoogle Scholar
Polifke, W. & Shtilman, L. 1989 The dynamics of helical decaying turbulence. Phys. Fluids A 1 (12), 2025–2033.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Praskovsky, A. A., Gledzer, E. B., Karyakin, M. Y. & Zhou, Y. 1993 The sweeping decorrelation hypothesis and energy–inertial scale interaction in high Reynolds number flows. J. Fluid Mech. 248, 493–511.CrossRefGoogle Scholar
Raupach, M. R. & Shaw, R. H. 1982 Averaging procedures for flow within vegetation canopies. Boundary-Layer Meteor. 22 (1), 79–90.CrossRefGoogle Scholar
Rodriguez, J. F. & Garcia, M. H. 2008 Laboratory measurements of 3-D flow patterns and turbulence in straight open channel with rough bed. J. Hydraul. Res. 46 (4), 454–465.CrossRefGoogle Scholar
Roy, A. G., Buffin-Bélanger, T., Lamarre, H. & Kirkbride, A. D. 2004 Size, shape and dynamics of large-scale turbulent flow structures in a gravel-bed river. J. Fluid Mech. 500, 1–27.CrossRefGoogle Scholar
Sanada, T. & Shanmugasundaram, V. 1992 Random sweeping effect in isotropic numerical turbulence. Phys. Fluids A 4 (6), 1245–1250.CrossRefGoogle Scholar
Smith, J. D. & McLean, S. R. 1977 Spatially averaged flow over a wavy surface. J. Geophys. Res. 82 (12), 1735–1746.CrossRefGoogle Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7 (11), 2778–2784.CrossRefGoogle Scholar
Sreenivasan, K. R. & Dhruva, B. 1998 Is there scaling in high-Reynolds-number turbulence? Prog. Theor. Phys. Suppl. 130, 103–120.CrossRefGoogle Scholar
Sukhodolov, A., Thiele, M. & Bungartz, H. 1998 Turbulence structure in a river reach with sand bed. Water Resour. Res. 34 (5), 1317–1334.CrossRefGoogle Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164, 476–490.CrossRefGoogle Scholar
Tchen, C. M. 1953 On the spectrum of energy in turbulent shear flow. J. Res. Natl Bur. Stand. 50, 51–62.CrossRefGoogle Scholar
Tchen, C. M. 1954 Transport processes as foundations of the Heisenberg and Obukhoff theories of turbulence. Phys. Rev. 93 (1), 4.CrossRefGoogle Scholar
Tennekes, H. 1975 Eulerian and Lagrangian time microscales in isotropic turbulence. J. Fluid Mech. 67 (03), 561–567.CrossRefGoogle Scholar
Theodorsen, T. 1952 Mechanism of turbulence. In Proceedings of the Second Midwestern Conference on Fluid Mechanics, pp. 1–18. Ohio State University.Google Scholar
Wan, M., Servidio, S., Oughton, S. & Matthaeus, W. H. 2009 The third-order law for increments in magnetohydrodynamic turbulence with constant shear. Phys. Plasmas 16 (9), 090703.CrossRefGoogle Scholar
Wan, M., Servidio, S., Oughton, S. & Matthaeus, W. H. 2010 The third-order law for magnetohydrodynamic turbulence with shear: numerical investigation. Phys. Plasmas 17 (5), 052307.CrossRefGoogle Scholar
Wilson, N. & Shaw, R. 1977 A higher order closure model for canopy flow. J. Appl. Meteorol. 16, 1197–1205.2.0.CO;2>CrossRefGoogle Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5.CrossRefGoogle Scholar
Yang, S.-Q. & Chow, A. T. 2008 Turbulence structures in non-uniform flows. Adv. Water Resour. 31 (10), 1344–1351.CrossRefGoogle Scholar