Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-20T21:50:52.726Z Has data issue: false hasContentIssue false
  • English
  • Français

Transport equations for the normalized nth-order moments of velocity derivatives in grid turbulence

Published online by Cambridge University Press:  16 November 2021

S.L. Tang Open the ORCID record for S.L. Tang [Opens in a new window] ,
R.A. Antonia  and
L. Djenidi Open the ORCID record for L. Djenidi [Opens in a new window]
S.L. Tang*
Affiliation:
Center for Turbulence Control, Harbin Institute of Technology, Shenzhen518055, PR China
R.A. Antonia
Affiliation:
School of Engineering, University of Newcastle, NSW2308, Australia
L. Djenidi
Affiliation:
School of Engineering, University of Newcastle, NSW2308, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

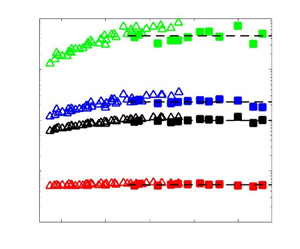
Transport equations for the normalized moments of the longitudinal velocity derivative ${F_{n + 1}}$ (here, $n$ is $1, 2, 3\ldots$) are derived from the Navier–Stokes (N–S) equations for shearless grid turbulence. The effect of the (large-scale) streamwise advection of ${F_{n + 1}}$ by the mean velocity on the normalized moments of the velocity derivatives can be expressed as $C_1 {F_{n + 1}}/Re_\lambda$, where $C_1$ is a constant and $Re_\lambda$ is the Taylor microscale Reynolds number. Transport equations for the normalized odd moments of the transverse velocity derivatives ${F_{y,n + 1}}$ (here, $n$ is 2, 4, 6), which should be zero if local isotropy is satisfied, are also derived and discussed in sheared and shearless grid turbulence. The effect of the (large-scale) streamwise advection term on the normalized moments of the velocity derivatives can also be expressed in the form $C_2 {F_{y,n + 1}}/Re_\lambda$, where $C_2$ is a constant. Finally, the contribution of the mean shear in the transport equation for ${F_{n + 1}}$ can be modelled as $15 B/Re_\lambda$, where $B$ ($=S^*{S_{s,n + 1}}$) is the product of the non-dimensional shear parameter $S^*$ and the normalized mixed longitudinal-transverse velocity derivatives ${{S_{s,n + 1}}}$; if local isotropy is satisfied, $S_{s,n + 1}$ should be zero. These results indicate that if ${F_{n + 1}}$, ${F_{y,n + 1}}$ and $B$ do not increase as rapidly as $Re_\lambda$, then the effect of the large-scale structures on small-scale turbulence will disappear when $Re_\lambda$ becomes sufficiently large.

JFM classification

Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 930 , 10 January 2022 , A31
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Antonia, R.A. & Browne, L.W.B. 1983 The destruction of temperature fluctuations in a turbulent plane jet. J. Fluid Mech. 134, 67–83.CrossRefGoogle Scholar
Antonia, R.A., Djenidi, L., Danaila, L. & Tang, S.L. 2017 Small scale turbulence and the finite Reynolds number effect. Phys. Fluids 29 (2), 020715.CrossRefGoogle Scholar
Antonia, R.A., Kim, J. & Browne, L.W.B. 1991 Some characteristics of small-scale turbulence in a turbulent duct flow. J. Fluid Mech. 233, 369–388.CrossRefGoogle Scholar
Antonia, R.A., Tang, S.L., Djenidi, L. & Danaila, L. 2015 Boundedness of the velocity derivative skewness in various turbulent flows. J. Fluid Mech. 781, 727–744.CrossRefGoogle Scholar
Batchelor, G.K. & Townsend, A.A. 1947 Decay of vorticity in isotropic turbulence. Proc. R. Soc. Lond. A 190, 534–550.Google Scholar
Browne, L.W., Antonia, R.A. & Shah, D.A. 1987 Turbulent energy dissipation in a wake. J. Fluid Mech. 179, 307–326.CrossRefGoogle Scholar
Danaila, L., Anselmet, F. & Antonia, R.A. 2002 An overview of the effect of large-scale inhomogeneities on small-scale turbulence. Phys. Fluids 14, 2475–2482.CrossRefGoogle Scholar
Danaila, L., Zhou, T., Anselmet, F. & Antonia, R.A. 2000 Calibration of a temperature dissipation probe in decaying grid turbulence. Exp. Fluids 28 (1), 45–50.CrossRefGoogle Scholar
Davidson, P.A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Djenidi, L., Antonia, R.A. & Tang, S.L. 2019 Scale invariance in finite Reynolds number homogeneous isotropic turbulence. J. Fluid Mech. 864, 244–272.CrossRefGoogle Scholar
Ferchichi, M. & Tavoularis, S. 2000 Reynolds number effects on the fine structure of uniformly sheared turbulence. Phys. Fluids 12, 2942–2953.CrossRefGoogle Scholar
Gibson, C.H., Stegen, G.R. & Williams, R.B. 1970 Statistics of the fine structure of turbulent velocity and temperature fields at high Reynolds number. J. Fluid Mech. 41, 153–167.CrossRefGoogle Scholar
Gotoh, T., Fukayama, D. & Nakano, T. 2002 Velocity field statistics in homogeneous steady turbulence obtained using a high-resolution direct numerical simulation. Phys. Fluids 14, 1065–1081.CrossRefGoogle Scholar
Gylfason, A., Ayyalasomayajula, S. & Warhaft, Z. 2004 Intermittency, pressure and acceleration statistics from hot-wire measurements in wind-tunnel turbulence. J. Fluid Mech. 501, 213–229.CrossRefGoogle Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–80.CrossRefGoogle Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.CrossRefGoogle Scholar
Kerr, R.M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.CrossRefGoogle Scholar
Kim, J. & Antonia, R.A. 1993 Isotropy of the small scales of turbulence at low Reynolds number. J. Fluid Mech. 251, 219–238.CrossRefGoogle Scholar
Kolmogorov, A.N. 1941 Local structure of turbulence in an incompressible fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Kolmogorov, A.N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.CrossRefGoogle Scholar
Lavoie, P., Burattini, P., Djenidi, L. & Antonia, R.A. 2005 Effect of initial conditions on decaying grid turbulence at low $R_{\lambda }$. Exp. Fluids 39, 865–874.CrossRefGoogle Scholar
Mestayer, P. 1982 Local isotropy and anisotropy in a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 125, 475–503.CrossRefGoogle Scholar
Pope, S.B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Saddoughi, S.G. & Veeravalli, S.V. 1994 Local isotropy of turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.CrossRefGoogle Scholar
Schumacher, J., Sreenivasan, K.R. & Yeung, P.K. 2003 Derivative moments in turbulent shear flows. Phys. Fluids 15, 84–90.CrossRefGoogle Scholar
Shen, X. & Warhaft, Z. 2000 The anisotropy of the small scale structure in high Reynolds number ($R_\lambda \sim 1000$) turbulent shear flow. Phys. Fluids 12, 2976–2989.CrossRefGoogle Scholar
Shen, X. & Warhaft, Z. 2002 Longitudinal and transverse structure functions in sheared and unsheared wind-tunnel turbulence. Phys. Fluids 14, 370–381.CrossRefGoogle Scholar
Siggia, E.D. 1981 Invariants for the one-point vorticity and strain rate correlation functions. Phys. Fluids 24, 1934–1936.CrossRefGoogle Scholar
Sreenivasan, K. & Antonia, R.A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.CrossRefGoogle Scholar
Tang, S.L., Antonia, R.A., Danaila, L., Djenidi, L., Zhou, T. & Zhou, Y. 2016 Towards local isotropy of higher-order statistics in the intermediate wake. Exp. Fluids 57, 111.CrossRefGoogle Scholar
Tang, S.L., Antonia, R.A., Djenidi, L., Abe, H., Zhou, T., Danaila, L. & Zhou, Y. 2015 a Transport equation for the mean turbulent energy dissipation rate on the centreline of a fully developed channel flow. J. Fluid Mech. 777, 151–177.CrossRefGoogle Scholar
Tang, S.L., Antonia, R.A., Djenidi, L., Danaila, L. & Zhou, Y. 2017 Finite Reynolds number effect on the scaling range behavior of turbulent longitudinal velocity structure functions. J. Fluid Mech. 820, 341–369.CrossRefGoogle Scholar
Tang, S.L., Antonia, R.A., Djenidi, L., Danaila, L. & Zhou, Y. 2018 Reappraisal of the velocity derivative flatness factor in various turbulent flows. J. Fluid Mech. 847, 244–265.CrossRefGoogle Scholar
Tang, S.L., Antonia, R.A., Djenidi, L. & Zhou, Y. 2015 b Transport equation for the isotropic turbulent energy dissipation rate in the far-wake of a circular cylinder. J. Fluid Mech. 784, 109–129.CrossRefGoogle Scholar
Tavoularis, S. & Corrsin, S. 1981 a Experiments in nearly homogeneous turbulent shear flow with a uniform mean temperature gradient. Part 2. The fine structure. J. Fluid Mech. 104, 349–367.CrossRefGoogle Scholar
Tavoularis, S. & Corrsin, S. 1981 b Experiments in nearly homogenous turbulent shear flow with a uniform mean temperature gradient. Part 1. J. Fluid Mech. 104, 311–347.CrossRefGoogle Scholar
Thiesset, F., Antonia, R.A. & Danaila, L. 2013 Scale-by-scale turbulent energy budget in the intermediate wake of two-dimensional generators. Phys. Fluids 25, 115105.CrossRefGoogle Scholar
Thiesset, F., Antonia, R.A. & Djenidi, L. 2014 Consequences of self-preservation on the axis of a turbulent round jet. J. Fluid Mech. 748, R2.CrossRefGoogle Scholar
Thiesset, F., Danaila, L. & Antonia, R.A. 2013 a Dynamical effect of the total strain induced by the coherent motion on local isotropy in a wake. J. Fluid Mech. 720, 393–423.CrossRefGoogle Scholar
Tsinober, A., Kit, E. & Dracos, T. 1992 Experimental investigation of the field of velocity gradients in turbulent flows. J. Fluid Mech. 242, 169–192.CrossRefGoogle Scholar
Van Atta, C.W. & Antonia, R.A. 1980 Reynolds number dependence of skewness and flatness factors of turbulent velocity derivatives. Phys. Fluids 23, 252–257.CrossRefGoogle Scholar
Vreman, A.W. & Kuerten, J.G.M. 2014 Statistics of spatial derivatives of velocity and pressure in turbulent channel flow. Phys. Fluids 26, 085103.CrossRefGoogle Scholar
Wyngaard, J.C. & Tennekes, H. 1970 Measurements of the small-scale structure of turbulence at moderate Reynolds numbers. Phys. Fluids 13, 1962–1969.CrossRefGoogle Scholar
Zhou, T. & Antonia, R.A. 2000 a Approximations for turbulent energy and temperature variance dissipation rates in grid turbulence. Phys. Fluids 12, 335–344.CrossRefGoogle Scholar
Zhou, T. & Antonia, R.A. 2000 b Reynolds number dependence of the small-scale structure of grid turbulence. J. Fluid Mech. 406, 81–107.CrossRefGoogle Scholar