Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T11:57:53.203Z Has data issue: false hasContentIssue false
  • English
  • Français

Transport by deep convection in basin-scale geostrophic circulation: turbulence-resolving simulations

Published online by Cambridge University Press:  26 February 2019

Catherine A. Vreugdenhil Open the ORCID record for Catherine A. Vreugdenhil [Opens in a new window] ,
Bishakhdatta Gayen Open the ORCID record for Bishakhdatta Gayen [Opens in a new window]  and
Ross W. Griffiths Open the ORCID record for Ross W. Griffiths [Opens in a new window]
Catherine A. Vreugdenhil*
Affiliation:
Research School of Earth Sciences, Australian National University, Canberra, ACT 2601, Australia
Bishakhdatta Gayen
Affiliation:
Research School of Earth Sciences, Australian National University, Canberra, ACT 2601, Australia
Ross W. Griffiths
Affiliation:
Research School of Earth Sciences, Australian National University, Canberra, ACT 2601, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations are used to investigate the nature of fully resolved small-scale convection and its role in large-scale circulation in a rotating 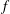$f$-plane rectangular basin with imposed surface temperature difference. The large-scale circulation has a horizontal geostrophic component and a deep vertical overturning. This paper focuses on convective circulation with no wind stress, and buoyancy forcing sufficiently strong to ensure turbulent convection within the thermal boundary layer (horizontal Rayleigh numbers 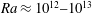$Ra\approx 10^{12}{-}10^{13}$). The dynamics are found to depend on the value of a convective Rossby number, $Ro_{\unicode[STIX]{x0394}T}$, which represents the strength of buoyancy forcing relative to Coriolis forces. Vertical convection shifts from a mean endwall plume under weak rotation (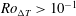$Ro_{\unicode[STIX]{x0394}T}>10^{-1}$) to ‘open ocean’ chimney convection plus mean vertical plumes at the side boundaries under strong rotation (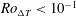$Ro_{\unicode[STIX]{x0394}T}<10^{-1}$). The overall heat throughput, horizontal gyre transport and zonally integrated overturning transport are then consistent with scaling predictions for flow constrained by thermal wind balance in the thermal boundary layer coupled to vertical advection–diffusion balance in the boundary layer. For small Rossby numbers relevant to circulation in an ocean basin, vertical heat transport from the surface layer into the deep interior occurs mostly in ‘open ocean’ chimney convection while most vertical mass transport is against the side boundaries. Both heat throughput and the mean circulation (in geostrophic gyres, boundary currents and overturning) are reduced by geostrophic constraints.

JFM classification

Geophysical and Geological Flows: Ocean circulation Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 865 , 25 April 2019 , pp. 681 - 719
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abernathey, R., Marshall, J. & Ferreira, D. 2011 The dependence of Southern Ocean meridional overturning on wind stress. J. Phys. Oceanogr. 41, 2261–2278.10.1175/JPO-D-11-023.1Google Scholar
Barkan, R., Winters, K. B. & Llewellyn Smith, S. G. 2013 Rotating horizontal convection. J. Fluid Mech. 723, 556–586.10.1017/jfm.2013.136Google Scholar
Boccaletti, G., Ferrari, R., Adcroft, A., Ferreira, D. & Marshall, J. 2005 The vertical structure of ocean heat transport. Geophys. Res. Lett. 32, L10603.10.1029/2005GL022474Google Scholar
Cenedese, C. 2012 Downwelling in basins subject to buoyancy loss. J. Phys. Oceanogr. 42, 1817–1833.10.1175/JPO-D-11-0114.1Google Scholar
Cessi, P. & Wolfe, C. L. 2009 Eddy-driven buoyancy gradients on eastern boundaries and their role in the thermocline. J. Phys. Oceanogr. 39 (7), 1595–1614.10.1175/2009JPO4063.1Google Scholar
Cessi, P., Young, W. R. & Polton, J. A. 2006 Control of large-scale heat transport by small-scale mixing. J. Phys. Oceanogr. 36, 1877–1894.10.1175/JPO2947.1Google Scholar
Coates, M. J. & Ivey, G. N. 1997 On convective turbulence and the influence of rotation. Dyn. Atmos. Oceans 25 (4), 217–232.10.1016/S0377-0265(96)00479-4Google Scholar
Ferrari, R. & Ferreira, D. 2011 What processes drive the ocean heat transport? Ocean Model. 38, 171–186.10.1016/j.ocemod.2011.02.013Google Scholar
Gayen, B., Griffiths, R. W. & Hughes, G. O. 2014 Stability transitions and turbulence in horizontal convection. J. Fluid Mech. 751, 698–724.10.1017/jfm.2014.302Google Scholar
Gayen, B., Griffiths, R. W., Hughes, G. O. & Saenz, J. A. 2013 Energetics of horizontal convection. J. Fluid Mech. 716, R10.10.1017/jfm.2012.592Google Scholar
Griffiths, R. W., Hughes, G. O. & Gayen, B. 2013 Horizontal convection dynamics: insights from transient adjustment. J. Fluid Mech. 726, 559–595.10.1017/jfm.2013.244Google Scholar
Helfrich, K. R. 1994 Thermals with background rotation and stratification. J. Fluid Mech. 259, 265–280.10.1017/S0022112094000121Google Scholar
Hignett, P., Ibbetson, A. & Killworth, P. D. 1981 On rotating thermal convection driven by non-uniform heating from below. J. Fluid Mech. 109, 161–187.10.1017/S0022112081000992Google Scholar
Hogg, A. McC., Spence, P., Saenko, O. A. & Downes, S. M. 2017 The energetics of Southern Ocean upwelling. J. Phys. Oceanogr. 47, 135–153.10.1175/JPO-D-16-0176.1Google Scholar
Hughes, G. O., Griffiths, R. W., Mullarney, J. C. & Peterson, W. H. 2007 A theoretical model for horizontal convection at high Rayleigh number. J. Fluid Mech. 581, 251–276.10.1017/S0022112007005630Google Scholar
Hughes, G. O., Hogg, A. M. & Griffiths, R. W. 2009 Available potential energy and irreversible mixing in the meridional overturning circulation. J. Phys. Oceanogr. 39, 3130–3146.10.1175/2009JPO4162.1Google Scholar
Hussam, W. K., Tsai, T. K. & Sheard, G. J. 2014 The effect of convection on radial horizontal convection and Nusselt number scaling in a cylindrical container. Intl J. Heat Mass Transfer 77, 46–59.10.1016/j.ijheatmasstransfer.2014.05.007Google Scholar
Jones, H. & Marshall, J. 1993 Convection with rotation in a neutral ocean: a study of open-ocean deep convection. J. Phys. Oceanogr. 23, 1009–1039.10.1175/1520-0485(1993)023<1009:CWRIAN>2.0.CO;22.0.CO;2>Google Scholar
Julien, K., Aurnou, J. M., Calkins, M. A., Knobloch, E., Marti, P., Stellmach, S. & Vasil, G. M. 2016 A nonlinear model for rotationally constrained convection with Ekman pumping. J. Fluid Mech. 798, 50–87.10.1017/jfm.2016.225Google Scholar
Julien, K., Rubio, A. M., Grooms, I. & Knobloch, E. 2012 Statistical and physical balances in low Rossby number Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 106 (4–5), 392–428.10.1080/03091929.2012.696109Google Scholar
Killworth, P. D 1983 Deep convection in the world ocean. Rev. Geophys. 21 (1), 1–26.10.1029/RG021i001p00001Google Scholar
King, E. M., Stellmach, S. & Aurnou, J. M. 2012 Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 691, 568–582.10.1017/jfm.2011.493Google Scholar
Kunnen, R., Stevens, R., Overkamp, J., Sun, C., Van Heijst, G. & Clercx, H. 2011 The role of Stewartson and Ekman layers in turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. 688, 422–442.10.1017/jfm.2011.383Google Scholar
Marotzke, J. & Scott, J. R 1999 Convective mixing and the thermohaline circulation. J. Phys. Oceanogr. 29 (11), 2962–2970.10.1175/1520-0485(1999)029<2962:CMATTC>2.0.CO;22.0.CO;2>Google Scholar
Marshall, J. & Radko, T. 2003 Residual-mean solutions for the antarctic circumpolar current and its associated overturning circulation. J. Phys. Oceanogr. 33, 2341–2354.10.1175/1520-0485(2003)033<2341:RSFTAC>2.0.CO;22.0.CO;2>Google Scholar
Marshall, J. & Schott, F. 1999 Open-ocean convection: observations, theory, and models. Rev. Geophys. 37, 1–64.10.1029/98RG02739Google Scholar
Maxworthy, T. & Narimousa, S. 1994 Unsteady, turbulent convection into a homogeneous, rotating fluid, with oceanographic applications. J. Phys. Oceanogr. 24, 865–887.10.1175/1520-0485(1994)024<0865:UTCIAH>2.0.CO;22.0.CO;2>Google Scholar
Morrison, A. K., Frölicher, T. L. & Sarmiento, J. L. 2015 Upwelling in the Southern Ocean. Phys. Today 68 (1), 27–32.10.1063/PT.3.2654Google Scholar
Morrison, A. K., Hogg, A. M. & Ward, M. L. 2011 Sensitivity of the Southern Ocean overturning circulation to surface buoyancy forcing. Geophys. Res. Lett. 38, L14602.10.1029/2011GL048031Google Scholar
Mullarney, J. C., Griffiths, R. W. & Hughes, G. O. 2004 Convection driven by differential heating at a horizontal boundary. J. Fluid Mech. 516, 181–209.10.1017/S0022112004000485Google Scholar
Nurser, A. J. G. & Lee, M. M. 2004 Isopycnal averaging at constant height. Part I: The formulation and a case study. J. Phys. Oceanogr. 34 (12), 2721–2739.10.1175/JPO2649.1Google Scholar
Nycander, J., Nilsson, J., Döös, K. & Broström, G. 2007 Thermodynamic analysis of ocean circulation. J. Phys. Oceanogr. 37 (8), 2038–2052.10.1175/JPO3113.1Google Scholar
Oort, A. H., Anderson, L. A. & Peixoto, J. P. 1994 Estimates of the energy cycle of the oceans. J. Geophys. Res. Oceans 99, 7665–7688.10.1029/93JC03556Google Scholar
Paparella, F. & Young, W. R. 2002 Horizontal convection is non-turbulent. J. Fluid Mech. 466, 205–214.10.1017/S0022112002001313Google Scholar
Park, Y.-G. & Whitehead, J. A. 1999 Rotating convection driven by differential bottom heating. J. Phys. Oceanogr. 29, 1208–1220.10.1175/1520-0485(1999)029<1208:RCDBDB>2.0.CO;22.0.CO;2>Google Scholar
Pedlosky, J. 2003 Thermally driven circulations in small oceanic basins. J. Phys. Oceanogr. 33 (11), 2333–2340.10.1175/1520-0485(2003)033<2333:TDCISO>2.0.CO;22.0.CO;2>Google Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 15, 135–167.10.1146/annurev.fluid.35.101101.161144Google Scholar
Pickart, R. S., Torres, D. J. & Clarke, R. A. 2001 Hydrography of the Labrador Sea during active convection. J. Phys. Oceanogr. 32, 428–457.10.1175/1520-0485(2002)032<0428:HOTLSD>2.0.CO;22.0.CO;2>Google Scholar
Plumley, M., Julien, K., Marti, P. & Stellmach, S. 2016 The effects of Ekman pumping on quasi-geostrophic Rayleigh–Bénard convection. J. Fluid Mech. 803, 51–71.10.1017/jfm.2016.452Google Scholar
Robinson, A. & Stommel, H. 1959 The oceanic thermocline and the associated thermohaline circulation. Tellus 11, 295–308.Google Scholar
Robinson, A. R. 1960 The general thermal circulation in equatorial regions. Deep-Sea Res. 6, 311–317.Google Scholar
Rosevear, M. G., Gayen, B. & Griffiths, R. W. 2017 Turbulent horizontal convection under spatially periodic forcing: a regime governed by interior inertia. J. Fluid Mech. 831, 491–523.10.1017/jfm.2017.640Google Scholar
Rossby, H. T. 1965 On thermal convection driven by non-uniform heating from below: an experimental study. Deep-Sea Res. 12, 9–16.Google Scholar
Saenz, J. A., Hogg, A. M., Hughes, G. O. & Griffiths, R. W. 2012 Mechanical power input from buoyancy and wind to the circulation in an ocean model. Geophys. Res. Lett. 39, L13605.10.1029/2012GL052035Google Scholar
Scotti, A. & White, B. 2014 Diagnosing mixing in stratified turbulent flows with a locally defined available potential energy. J. Fluid Mech. 740, 114–135.10.1017/jfm.2013.643Google Scholar
Send, U. & Marshall, J. 1995 Integral effects of deep convection. J. Phys. Oceanogr. 25, 855–872.10.1175/1520-0485(1995)025<0855:IEODC>2.0.CO;22.0.CO;2>Google Scholar
Sohail, T., Gayen, B. & Hogg, A. McC. 2018 Convection enhances mixing in the Southern Ocean. Geophys. Res. Lett. 45, 4198–4207.10.1029/2018GL077711Google Scholar
Spall, M. A. 2003 On the thermohaline circulation in flat bottom marginal seas. J. Mar. Res. 61 (1), 1–25.10.1357/002224003321586390Google Scholar
Spall, M. A. 2010 Dynamics of downwelling in an eddy-resolving convective basin. J. Phys. Oceanogr. 40 (10), 2341–2347.10.1175/2010JPO4465.1Google Scholar
Spall, M. A. 2011 On the role of eddies and surface forcing in the heat transport and overturning circulation in marginal seas. J. Clim. 24 (18), 4844–4858.10.1175/2011JCLI4130.1Google Scholar
Stevens, R., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.10.1017/S0022112009992461Google Scholar
Stewart, K. D., Hughes, G. O. & Griffiths, R. W. 2011 When do marginal seas and topographic sills modify the ocean density structure? J. Geophys. Res. 116, C08021.10.1029/2011JC006980Google Scholar
Stewartson, K. 1957 On almost rigid rotations. J. Fluid Mech. 3, 17–26.10.1017/S0022112057000452Google Scholar
Stewartson, K. 1966 On almost rigid rotations. Part 2. J. Fluid Mech. 26, 131–144.10.1017/S0022112066001137Google Scholar
Stommel, H. 1962 On the smallness of sinking regions in the ocean. Proc. Natl Acad. Sci. USA 48, 766–772.10.1073/pnas.48.5.766Google Scholar
Tailleux, R. 2009 On the energetics of stratified turbulent mixing, irreversible thermodynamics, Boussinesq models and the ocean heat engine controversy. J. Fluid Mech. 638, 339–382.10.1017/S002211200999111XGoogle Scholar
Tailleux, R. 2013 Irreversible compressible work and available potential energy dissipation in turbulent stratified fluids. Phys. Scr. 2013 (T155), 014033.Google Scholar
Tailleux, R.2018 APE dissipation is a form of Joule heating. It is irreversible, not reversible. arXiv:1806.11303.Google Scholar
Talley, L. D. 2003 Shallow, intermediate, and deep overturning components of the global heat budget. J. Phys. Oceanogr. 33 (3), 530–560.10.1175/1520-0485(2003)033<0530:SIADOC>2.0.CO;22.0.CO;2>Google Scholar
Våge, K., Pickart, R. S., Thierry, V., Reverdin, G. & Lee, C. M. 2009 Surprising return of deep convection to the subpolar North Atlantic Ocean in winter 2007–2008. Nat. Geosci. 2, 67–72.10.1038/ngeo382Google Scholar
Van Heijst, G. J. F. 1983 The shear-layer structure in a rotating fluid near a differentially rotating sidewall. J. Fluid Mech. 130, 1–12.10.1017/S0022112083000932Google Scholar
Vreugdenhil, C. A., Gayen, B. & Griffiths, R. W. 2016 Mixing and dissipation in a geostrophic buoyancy-driven circulation. J. Geophys. Res. Oceans 121, 6076–6091.10.1002/2016JC011691Google Scholar
Vreugdenhil, C. A., Griffiths, R. W. & Gayen, B. 2017 Geostrophic and chimney regimes in rotating horizontal convection with imposed heat flux. J. Fluid Mech. 823, 57–99.10.1017/jfm.2017.249Google Scholar
Winters, K. B, Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.10.1017/S002211209500125XGoogle Scholar
Winton, M. 1995 Why is the deep sinking narrow? J. Phys. Oceanogr. 25, 997–1005.10.1175/1520-0485(1995)025<0997:WITDSN>2.0.CO;22.0.CO;2>Google Scholar
Zemskova, V. E., White, B. L. & Scotti, A. 2015 Available potential energy and the general circulation: partitioning wind, buoyancy forcing, and diapycnal mixing. J. Phys. Oceanogr. 45 (6), 1510–1531.10.1175/JPO-D-14-0043.1Google Scholar