Published online by Cambridge University Press: 09 February 2015
Direct numerical simulations (DNS) of turbulent stratified flow in an open channel with an internal heat source following the Beer–Lambert law from the surface are used to investigate the transition from neutral to strongly stable flow. Our buoyancy bulk parameter is defined through the ratio of the domain height
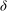 ${\it\delta}$
to
${\it\delta}$
to
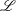 $\mathscr{L}$
, a bulk Obukhov length scale for the flow. We cover the range
$\mathscr{L}$
, a bulk Obukhov length scale for the flow. We cover the range
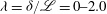 ${\it\lambda}={\it\delta}/\mathscr{L}=0{-}2.0$
, from neutral conditions to the onset of the stable regime, with the Reynolds number range
${\it\lambda}={\it\delta}/\mathscr{L}=0{-}2.0$
, from neutral conditions to the onset of the stable regime, with the Reynolds number range
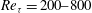 $Re_{{\it\tau}}=200{-}800$
, at a Prandtl number of 0.71. The result is a boundary layer flow where the effects of stratification are weak in the wall region but progressively stronger in the outer layer up to the free surface. At
$Re_{{\it\tau}}=200{-}800$
, at a Prandtl number of 0.71. The result is a boundary layer flow where the effects of stratification are weak in the wall region but progressively stronger in the outer layer up to the free surface. At
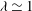 ${\it\lambda}\simeq 1$
the turbulent kinetic energy (TKE) budget is in local equilibrium over a region extending from the near-wall region to a free-surface affected region a distance
${\it\lambda}\simeq 1$
the turbulent kinetic energy (TKE) budget is in local equilibrium over a region extending from the near-wall region to a free-surface affected region a distance
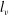 $l_{{\it\nu}}$
from the surface, with
$l_{{\it\nu}}$
from the surface, with
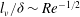 $l_{{\it\nu}}/{\it\delta}\sim Re^{-1/2}$
. In this equilibrium region the flow can be characterised by the flux Richardson number
$l_{{\it\nu}}/{\it\delta}\sim Re^{-1/2}$
. In this equilibrium region the flow can be characterised by the flux Richardson number
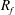 $R_{f}$
and the local Obukhov length scale
$R_{f}$
and the local Obukhov length scale
 ${\it\Lambda}$
. At higher
${\it\Lambda}$
. At higher
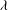 ${\it\lambda}$
local mixing limit conditions are observed over an extended region. At
${\it\lambda}$
local mixing limit conditions are observed over an extended region. At
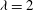 ${\it\lambda}=2$
the flux Richardson number approaches critical limit values of
${\it\lambda}=2$
the flux Richardson number approaches critical limit values of
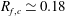 $R_{f,c}\simeq 0.18$
and gradient Richardson number
$R_{f,c}\simeq 0.18$
and gradient Richardson number
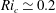 $Ri_{c}\simeq 0.2$
. At high
$Ri_{c}\simeq 0.2$
. At high
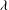 ${\it\lambda}$
, we obtain a flow field where buoyancy interacts with the smallest scales of motion and the turbulent shear stress and buoyancy flux are suppressed to molecular levels. We find that this regime can be identified in terms of the parameter
${\it\lambda}$
, we obtain a flow field where buoyancy interacts with the smallest scales of motion and the turbulent shear stress and buoyancy flux are suppressed to molecular levels. We find that this regime can be identified in terms of the parameter
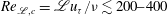 $Re_{\mathscr{L},c}=\mathscr{L}u_{{\it\tau}}/{\it\nu}\lesssim 200{-}400$
(where
$Re_{\mathscr{L},c}=\mathscr{L}u_{{\it\tau}}/{\it\nu}\lesssim 200{-}400$
(where
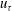 $u_{{\it\tau}}$
is the friction velocity and
$u_{{\it\tau}}$
is the friction velocity and
 ${\it\nu}$
the kinematic viscosity), which is related to the
${\it\nu}$
the kinematic viscosity), which is related to the
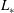 $L_{\ast }$
parameter of Flores and Riley (Boundary-Layer Meteorol., vol. 139 (2), 2011, pp. 241–259) and buoyancy Reynolds number
$L_{\ast }$
parameter of Flores and Riley (Boundary-Layer Meteorol., vol. 139 (2), 2011, pp. 241–259) and buoyancy Reynolds number
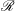 $\mathscr{R}$
. With energetic equilibrium attained, the local buoyancy Reynolds number,
$\mathscr{R}$
. With energetic equilibrium attained, the local buoyancy Reynolds number,
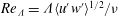 $Re_{{\it\Lambda}}={\it\Lambda}\langle u^{\prime }w^{\prime }\rangle ^{1/2}/{\it\nu}$
, is directly related to the separation of the Ozmidov (
$Re_{{\it\Lambda}}={\it\Lambda}\langle u^{\prime }w^{\prime }\rangle ^{1/2}/{\it\nu}$
, is directly related to the separation of the Ozmidov (
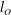 $l_{O}$
) and Kolmogorov (
$l_{O}$
) and Kolmogorov (
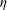 ${\it\eta}$
) length scales in the outer boundary layer by
${\it\eta}$
) length scales in the outer boundary layer by
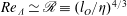 $Re_{{\it\Lambda}}\simeq \mathscr{R}\equiv (l_{O}/{\it\eta})^{4/3}$
. The inner wall region has the behaviour
$Re_{{\it\Lambda}}\simeq \mathscr{R}\equiv (l_{O}/{\it\eta})^{4/3}$
. The inner wall region has the behaviour
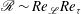 $\mathscr{R}\sim Re_{\mathscr{L}}Re_{{\it\tau}}$
, in contrast to stratified boundary layer flows where the buoyancy flux is non-zero at the wall and
$\mathscr{R}\sim Re_{\mathscr{L}}Re_{{\it\tau}}$
, in contrast to stratified boundary layer flows where the buoyancy flux is non-zero at the wall and
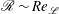 $\mathscr{R}\sim Re_{\mathscr{L}}$
.
$\mathscr{R}\sim Re_{\mathscr{L}}$
.