Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-20T16:45:47.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades

Published online by Cambridge University Press:  27 October 2014

Adrián Lozano-Durán  and
Javier Jiménez
Adrián Lozano-Durán*
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, 28040 Madrid, Spain
Javier Jiménez
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, 28040 Madrid, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A novel approach to the study of the kinematics and dynamics of turbulent flows is presented. The method involves tracking in time coherent structures, and provides all of the information required to characterize eddies from birth to death. Spatially and temporally well-resolved DNSs of channel data at 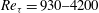$\mathit{Re}_{{\it\tau}}=930{-}4200$ are used to analyse the evolution of three-dimensional sweeps, ejections (Lozano-Durán et al., J. Fluid Mech., vol. 694, 2012, pp. 100–130) and clusters of vortices (del Álamo et al., J. Fluid Mech., vol. 561, 2006, pp. 329–358). The results show that most of the eddies remain small and do not last for long times, but that some become large, attach to the wall and extend across the logarithmic layer. The latter are geometrically and temporally self-similar, with lifetimes proportional to their size (or distance from the wall), and their dynamics is controlled by the mean shear near their centre of gravity. They are responsible for most of the total momentum transfer. Their origin, eventual disappearance, and history are investigated and characterized, including their advection velocity at different wall distances and the temporal evolution of their size. Reinforcing previous results, the symmetry found between sweeps and ejections supports the idea that they are not independent structures, but different manifestations of larger quasi-streamwise rollers in which they are embedded. Spatially localized direct and inverse cascades are respectively associated with the splitting and merging of individual structures, as in the models of Richardson (Proc. R. Soc. Lond. A, vol. 97(686), 1920, pp. 354–373) or Obukhov (Izv. Akad. Nauk USSR, Ser. Geogr. Geofiz., vol. 5(4), 1941, pp. 453–466). It is found that the direct cascade predominates, but that both directions are roughly comparable. Most of the merged or split fragments have sizes of the order of a few Kolmogorov viscous units, but a substantial fraction of the growth and decay of the larger eddies is due to a self-similar inertial process in which eddies merge and split in fragments spanning a wide range of scales.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 759 , 25 November 2014 , pp. 432 - 471
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acarlar, M. S. & Smith, C. R. 1987a A study of hairpin vortices in a laminar boundary layer. Part 1. Hairpin vortices generated by a hemisphere protuberance. J. Fluid Mech. 175, 1–41.Google Scholar
Acarlar, M. S. & Smith, C. R. 1987b A study of hairpin vortices in a laminar boundary layer. Part 2. Hairpin vortices generated by fluid injection. J. Fluid Mech. 175, 43–83.Google Scholar
Adrian, R. J. 1991 Particle-imaging techniques for experimental fluid mechanics. Annu. Rev. Fluid Mech. 23 (1), 261–304.CrossRefGoogle Scholar
Adrian, R. 2005 Twenty years of particle image velocimetry. Exp. Fluids 39 (2), 159–169.Google Scholar
Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Aoyama, T., Ishihara, T., Kaneda, Y., Yokokawa, M. & Un, A. 2005 Statistics of energy transfer in high-resolution direct numerical simulation of turbulence in a periodic box. J. Phys. Soc. Japan 74, 3202–3212.Google Scholar
Bernard, P. S. 2013 Vortex dynamics in transitional and turbulent boundary layers. AIAA J. 51 (8), 1828–1842.Google Scholar
Blackwelder, R. F. & Kaplan, R. E. 1976 On the wall structure of the turbulent boundary layer. J. Fluid Mech. 76, 89–112.CrossRefGoogle Scholar
Bogard, D. G. & Tiederman, W. G. 1986 Burst detection with single-point velocity measurements. J. Fluid Mech. 162, 389–413.Google Scholar
Bradshaw, P. 1967 Inactive motions and pressure fluctuations in turbulent boundary layers. J. Fluid Mech. 30, 241–258.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.Google Scholar
Cadot, O., Douady, S. & Couder, Y. 1995 Characterization of the low-pressure filaments in a three-dimensional turbulent shear flow. Phys. Fluids 7 (3), 630–646.Google Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids 2 (5), 765–777.Google Scholar
Christensen, K. T. & Adrian, R. J. 2000 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.CrossRefGoogle Scholar
Cimarelli, A., de Angelis, E. & Casciola, C. M. 2013 Paths of energy in turbulent channel flows. J. Fluid Mech. 715, 436–451.CrossRefGoogle Scholar
Corino, E. R. & Brodkey, R. S. 1969 A visual investigation of the wall region in turbulent flow. J. Fluid Mech. 37, 1–30.CrossRefGoogle Scholar
Corrsin, S.1958 Local isotropy in turbulent shear flow. Res. Memo 58B11. NACA.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011a Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.CrossRefGoogle Scholar
Dennis, D. J. C. & Nickels, T. B. 2011b Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.CrossRefGoogle Scholar
Elsinga, G. E. & Marusic, I. 2010 Evolution and lifetimes of flow topology in a turbulent boundary layer. Phys. Fluids 22 (1), 015102.Google Scholar
Elsinga, G. E., Poelma, C., Schröder, A., Geisler, R., Scarano, F. & Westerweel, J. 2012 Tracking of vortices in a turbulent boundary layer. J. Fluid Mech. 697, 273–295.Google Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22 (7), 071704.CrossRefGoogle Scholar
Flores, O., Jiménez, J. & del Álamo, J. C. 2007 Vorticity organization in the outer layer of turbulent channels with disturbed walls. J. Fluid Mech. 591, 145–154.CrossRefGoogle Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Guezennec, Y. G., Piomelli, U. & Kim, J. 1989 On the shape and dynamics of wall structures in turbulent channel flow. Phys. Fluids 1 (4), 764–766.Google Scholar
Haidari, A. H. & Smith, C. R. 1994 The generation and regeneration of single hairpin vortices. J. Fluid Mech. 277, 135–162.Google Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $\mathit{Re}_{{\it\tau}}=2003$ . Phys. Fluids 18 (1), 011702.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Jiménez, J.1998 The largest scales of turbulence. In CTR Ann. Res. Briefs, Stanford University, pp. 137–154.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.CrossRefGoogle Scholar
Jiménez, J. 2013a How linear is wall-bounded turbulence? Phys. Fluids 25, 110814.Google Scholar
Jiménez, J. 2013b Near-wall turbulence. Phys. Fluids 25 (10), 101302.CrossRefGoogle Scholar
Jiménez, J., del Álamo, J. C. & Flores, O. 2004 The large-scale dynamics of near-wall turbulence. J. Fluid Mech. 505, 179–199.Google Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.Google Scholar
Jiménez, J., Kawahara, G., Simens, M. P., Nagata, M. & Shiba, M. 2005 Characterization of near-wall turbulence in terms of equilibrium and ‘bursting’ solutions. Phys. Fluids 17 (1), 015105.Google Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Jiménez, J. & Wray, A. A. 1998 On the characteristics of vortex filaments in isotropic turbulence. J. Fluid Mech. 373, 255–285.Google Scholar
Jiménez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.Google Scholar
Johansson, A. V., Alfredsson, P. H. & Kim, J. 1991 Evolution and dynamics of shear-layer structures in near-wall turbulence. J. Fluid Mech. 224, 579–599.CrossRefGoogle Scholar
Kawahara, G., Uhlmann, M. & van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 44 (1), 203–225.Google Scholar
Kim, K. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Kim, J. & Hussain, F. 1993 Propagation velocity of perturbations in turbulent channel flow. Phys. Fluids 5 (3), 695–706.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds’ numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Krogstad, P.-A., Kaspersen, J. H. & Rimestad, S. 1998 Convection velocities in a turbulent boundary layer. Phys. Fluids 10 (4), 949–957.Google Scholar
Kuglin, C. D. & Hines, D. C.1975 The phase correlation image alignment method. In Proceeding of IEEE International Conference on Cybernetics and Society, pp. 163–165.Google Scholar
LeHew, J., Guala, M. & McKeon, B. 2013 Time-resolved measurements of coherent structures in the turbulent boundary layer. Exp. Fluids 54 (4), 1–16.Google Scholar
Leith, C. E. 1967 Diffusion approximation to inertial energy transfer in isotropic turbulence. Phys. Fluids 10, 1409–1416.Google Scholar
Lesieur, M. 1991 Turbulence in Fluids, 2nd edn. Springer.Google Scholar
Lozano-Durán, A., Flores, O. & Jiménez, J. 2012 The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 694, 100–130.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2010 Time-resolved evolution of the wall-bounded vorticity cascade. In Proceedings Div. Fluid Dyn., p. EB-3. American Physical Society.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2011 Time-resolved evolution of the wall-bounded vorticity cascade. J. Phys.: Conf. Ser. 318 (6), 062016.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to $\mathit{Re}_{{\it\tau}}=4200$ . Phys. Fluids 26 (1), 011702.CrossRefGoogle Scholar
Lu, S. S. & Willmarth, W. W. 1973 Measurements of the structure of the Reynolds stress in a turbulent boundary layer. J. Fluid Mech. 60, 481–511.Google Scholar
Martín, J., Ooi, A., Chong, M. S. & Soria, J. 1998 Dynamics of the velocity gradient tensor invariants in isotropic turbulence. Phys. Fluids 10 (9), 2336–2346.Google Scholar
Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13 (3), 735–743.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
McKeon, B. & Sreenivasan, K. 2007 Introduction: scaling and structure in high Reynolds number wall-bounded flows. Phil. Trans. R. Soc. A 365 (1852), 635–646.Google Scholar
Mizuno, Y. & Jiménez, J. 2013 Wall turbulence without walls. J. Fluid Mech. 723, 429–455.Google Scholar
Moisy, F. & Jiménez, J. 2004 Geometry and clustering of intense structures in isotropic turbulence. J. Fluid Mech. 513, 111–133.Google Scholar
Nickels, T. B. & Marusic, I. 2001 On the different contributions of coherent structures to the spectra of a turbulent round jet and a turbulent boundary layer. J. Fluid Mech. 448, 367–385.Google Scholar
Obukhov, A. M. 1941 On the distribution of energy in the spectrum of turbulent flow. Izv. Akad. Nauk USSR, Ser. Geogr. Geofiz. 5 (4), 453–466.Google Scholar
Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41, 363–386.CrossRefGoogle Scholar
Panton, R. L. 2001 Overview of the self-sustaining mechanisms of wall turbulence. Prog. Aerosp. Sci. 37 (4), 341–383.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E. & Chong, M. S. 1994 Topology of flow patterns in vortex motions and turbulence. Appl. Sci. Res. 53 (3–4), 357–374.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Piomelli, U., Cabot, W. H., Moin, P. & Lee, S. 1991 Subgrid-scale backscatter in turbulent and transitional flows. Phys. Fluids 3 (7), 1766–1771.Google Scholar
Pirozzoli, S. 2011 Flow organization near shear layers in turbulent wall-bounded flows. J. Turbul. 01, N41.Google Scholar
Richardson, L. F. 1920 The supply of energy from and to atmospheric eddies. Proc. R. Soc. Lond. A 97 (686), 354–373.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.Google Scholar
Rogers, M. M. & Moin, P. 1987 The structure of the vorticity field in homogeneous turbulent flows. J. Fluid Mech. 176, 33–66.Google Scholar
Saddoughi, S. G. & Veeravali, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds numbers. J. Fluid Mech. 268, 333–372.Google Scholar
Schlatter, P., Li, Q., Örlü, R., Hussain, F. & Henningson, D. 2014 On the near-wall vortical structures at moderate Reynolds numbers. Eur. J. Mech. (B/Fluids) 48, 75–93.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Singer, B. A. & Joslin, R. D. 1994 Metamorphosis of a hairpin vortex into a Young turbulent spot. Phys. Fluids 6 (11), 3724–3736.Google Scholar
Suponitsky, V., Avital, E. & Gaster, M. 2005 On three-dimensionality and control of incompressible cavity flow. Phys. Fluids 17 (10), 104103.CrossRefGoogle Scholar
Sutton, M. A., Wolters, W. J., Peters, W. H., Ranson, W. F. & McNeill, S. R. 1983 Determination of displacements using an improved digital correlation method. Image Vis. Comput. 1 (3), 133–139.Google Scholar
Tanahashi, M., Kang, S., Miyamoto, T. & Shiokawa, S. 2004 Scaling law of fine scale eddies in turbulent channel flows up to $\mathit{Re}_{{\it\tau}}=800$ . Intl J. Heat Fluid Flow 25, 331–341.Google Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. 164, 476–490.Google Scholar
Theodorsen, T.1952 Mechanism of turbulence. In Proceedings of 2nd Midwestern Conference of Fluid Mechanics, Ohio State University.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Townsend, A. A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11, 97–120.CrossRefGoogle Scholar
Tuerke, F. & Jiménez, J. 2013 Simulations of turbulent channels with prescribed velocity profiles. J. Fluid Mech. 723, 587–603.Google Scholar
Villermaux, E., Sixou, B. & Gagne, Y. 1995 Intense vortical structures in grid-generated turbulence. Phys. Fluids 7 (8), 2008–2013.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54, 39–48.Google Scholar
Willert, C. E. & Gharib, M. 1991 Digital particle image velocimetry. Exp. Fluids 10, 181–193.Google Scholar
Willmarth, W. W. & Lu, S. S. 1972 Structure of the Reynolds stress near the wall. J. Fluid Mech. 55, 65–92.Google Scholar
Wills, J. 1964 On convection velocities in turbulent shear flows. J. Fluid Mech. 20, 417–432.Google Scholar
Wu, X. & Moin, P. 2010 Transitional and turbulent boundary layer with heat transfer. Phys. Fluids 22, 085105.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar
Supplementary material: PDF

Lozano-Durán and Jiménez supplementary material

Appendix

Download Lozano-Durán and Jiménez supplementary material(PDF)
PDF 172.9 KB