Article contents
Tilting at wave beams: a new perspective on the St. Andrew’s Cross
Published online by Cambridge University Press: 05 October 2017
Abstract
The generation of internal gravity waves by a vertically oscillating cylinder that is tilted to the horizontal in a stratified Boussinesq fluid of constant buoyancy frequency,  $N$, is investigated. This variant of the widely studied horizontal configuration – where a cylinder aligned with a plane of constant gravitational potential induces four wave beams that emanate from the cylinder, forming a cross pattern known as the ‘St. Andrew’s Cross’ – brings out certain unique features of radiated internal waves from a line source tilted to the horizontal. Specifically, simple kinematic considerations reveal that for a cylinder inclined by a given angle
$N$, is investigated. This variant of the widely studied horizontal configuration – where a cylinder aligned with a plane of constant gravitational potential induces four wave beams that emanate from the cylinder, forming a cross pattern known as the ‘St. Andrew’s Cross’ – brings out certain unique features of radiated internal waves from a line source tilted to the horizontal. Specifically, simple kinematic considerations reveal that for a cylinder inclined by a given angle 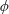 $\unicode[STIX]{x1D719}$ to the horizontal, there is a cutoff frequency,
$\unicode[STIX]{x1D719}$ to the horizontal, there is a cutoff frequency, 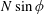 $N\sin \unicode[STIX]{x1D719}$, below which there is no longer a radiated wave field. Furthermore, three-dimensional effects due to the finite length of the cylinder, which are minor in the horizontal configuration, become a significant factor and eventually dominate the wave field as the cutoff frequency is approached; these results are confirmed by supporting laboratory experiments. The kinematic analysis, moreover, suggests a resonance phenomenon near the cutoff frequency as the group-velocity component perpendicular to the cylinder direction vanishes at cutoff; as a result, energy cannot be easily radiated away from the source, and nonlinear and viscous effects are likely to come into play. This scenario is examined by adapting the model for three-dimensional wave beams developed in Kataoka & Akylas (J. Fluid Mech., vol. 769, 2015, pp. 621–634) to the near-resonant wave field due to a tilted line source of large but finite length. According to this model, the combination of three-dimensional, nonlinear and viscous effects near cutoff triggers transfer of energy, through the action of Reynolds stresses, to a circulating horizontal mean flow. Experimental evidence of such an induced mean flow near cutoff is also presented.
$N\sin \unicode[STIX]{x1D719}$, below which there is no longer a radiated wave field. Furthermore, three-dimensional effects due to the finite length of the cylinder, which are minor in the horizontal configuration, become a significant factor and eventually dominate the wave field as the cutoff frequency is approached; these results are confirmed by supporting laboratory experiments. The kinematic analysis, moreover, suggests a resonance phenomenon near the cutoff frequency as the group-velocity component perpendicular to the cylinder direction vanishes at cutoff; as a result, energy cannot be easily radiated away from the source, and nonlinear and viscous effects are likely to come into play. This scenario is examined by adapting the model for three-dimensional wave beams developed in Kataoka & Akylas (J. Fluid Mech., vol. 769, 2015, pp. 621–634) to the near-resonant wave field due to a tilted line source of large but finite length. According to this model, the combination of three-dimensional, nonlinear and viscous effects near cutoff triggers transfer of energy, through the action of Reynolds stresses, to a circulating horizontal mean flow. Experimental evidence of such an induced mean flow near cutoff is also presented.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 2
- Cited by



