Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T21:02:44.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional wake transition of a square cylinder

Published online by Cambridge University Press:  06 March 2018

Hongyi Jiang Open the ORCID record for Hongyi Jiang [Opens in a new window] ,
Liang Cheng  and
Hongwei An
Hongyi Jiang
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
Liang Cheng*
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian, 116024, China
Hongwei An
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

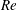Three-dimensional (3-D) wake transition for flow past a square cylinder aligned with sides perpendicular and parallel to the approaching flow is investigated using direct numerical simulation. The secondary wake instability, namely a Mode A instability, occurs at a Reynolds number ($Re$) of 165.7. A gradual wake transition from Mode A* (i.e. Mode A with vortex dislocations) to Mode B is observed over a range of 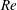$Re$ from 185 to 210, within which the probability of occurrence of vortex dislocations decreases monotonically with increasing 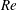$Re$. The characteristics of the Strouhal–Reynolds number relationship are analysed. At the onset of Mode A*, a sudden drop of the 3-D Strouhal number from its two-dimensional counterpart is observed, which is due to the subcritical nature of the Mode A* instability. A continuous 3-D Strouhal–Reynolds number curve is observed over the mode swapping regime, since Mode A* and Mode B have extremely close vortex shedding frequencies and therefore only a single merged peak is observed in the frequency spectrum. The existence of hysteresis for the Mode A and Mode B wake instabilities is examined. The unconfined Mode A and Mode B wake instabilities are hysteretic and non-hysteretic, respectively. However, a spanwise confined Mode A could be non-hysteretic. It is proposed that the existence of hysteresis at a wake instability can be identified by examining the sudden/gradual variation of the 3-D flow properties at the onset of the wake instability, with sudden and gradual variations corresponding to hysteretic (subcritical) and non-hysteretic (supercritical) flows, respectively.

JFM classification

Vortex Flows: Vortex instability Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 842 , 10 May 2018 , pp. 102 - 127
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akbar, T., Bouchet, G. & Dušek, J. 2011 Numerical investigation of the subcritical effects at the onset of three-dimensionality in the circular cylinder wake. Phys. Fluids 23, 094103.CrossRefGoogle Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Blackburn, H. M. & Lopez, J. M. 2003 On three-dimensional quasiperiodic Floquet instabilities of two-dimensional bluff body wakes. Phys. Fluids 15, L57–L60.CrossRefGoogle Scholar
Carmo, B. S., Sherwin, S. J., Bearman, P. W. & Willden, R. H. J. 2008 Wake transition in the flow around two circular cylinders in staggered arrangements. J. Fluid Mech. 597, 1–29.CrossRefGoogle Scholar
Carmo, B. S., Meneghini, J. R. & Sherwin, S. J. 2010 Secondary instabilities in the flow around two circular cylinders in tandem. J. Fluid Mech. 644, 395–431.CrossRefGoogle Scholar
Choi, C., Jang, Y. & Yang, K. 2012 Secondary instability in the near-wake past two tandem square cylinders. Phys. Fluids 24, 024102.CrossRefGoogle Scholar
Dušek, J., Le Gal, P. & Fraunié, P. 1994 A numerical and theoretical study of the first Hopf bifurcation in a cylinder wake. J. Fluid Mech. 264, 59–80.CrossRefGoogle Scholar
Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.CrossRefGoogle Scholar
Henderson, R. D. & Barkley, D. 1996 Secondary instability in the wake of a circular cylinder. Phys. Fluids 8, 1683–1685.CrossRefGoogle Scholar
Issa, R. I. 1986 Solution of implicitly discretized fluid flow equations by operator-splitting. J. Comput. Phys. 62, 40–65.CrossRefGoogle Scholar
Jiang, H. & Cheng, L. 2017 Strouhal–Reynolds number relationship for flow past a circular cylinder. J. Fluid Mech. 832, 170–188.CrossRefGoogle Scholar
Jiang, H., Cheng, L., Draper, S., An, H. & Tong, F. 2016 Three-dimensional direct numerical simulation of wake transitions of a circular cylinder. J. Fluid Mech. 801, 353–391.CrossRefGoogle Scholar
Jiang, H., Cheng, L. & An, H. 2017a On numerical aspects of simulating flow past a circular cylinder. Intl J. Numer. Meth. Fluids 85, 113–132.CrossRefGoogle Scholar
Jiang, H., Cheng, L., Draper, S. & An, H. 2017b Prediction of the secondary wake instability of a circular cylinder with direct numerical simulation. Comput. Fluids 149, 172–180.CrossRefGoogle Scholar
Jiang, H., Cheng, L., Draper, S. & An, H. 2017c Two- and three-dimensional instabilities in the wake of a circular cylinder near a moving wall. J. Fluid Mech. 812, 435–462.CrossRefGoogle Scholar
Jiang, H., Cheng, L., Draper, S. & An, H. 2017d Three-dimensional wake transition for a circular cylinder near a moving wall. J. Fluid Mech. 818, 260–287.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1976 Mechanics, 3rd edn. Pergamon.Google Scholar
Leweke, T. & Williamson, C. H. K. 1998 Three-dimensional instabilities in wake transition. Eur. J. Mech. (B/Fluids) 17, 571–586.CrossRefGoogle Scholar
Luo, S. C., Chew, Y. T. & Ng, Y. T. 2003 Characteristics of square cylinder wake transition flows. Phys. Fluids 15, 2549–2559.CrossRefGoogle Scholar
Luo, S. C., Tong, X. H. & Khoo, B. C. 2007 Transition phenomena in the wake of a square cylinder. J. Fluids Struct. 23, 227–248.CrossRefGoogle Scholar
Park, D. & Yang, K. 2016 Flow instabilities in the wake of a rounded square cylinder. J. Fluid Mech. 793, 915–932.CrossRefGoogle Scholar
Robichaux, J., Balachandar, S. & Vanka, S. P. 1999 Three-dimensional Floquet instability of the wake of square cylinder. Phys. Fluids 11, 560–578.CrossRefGoogle Scholar
Saha, A. K., Muralidhar, K. & Biswas, G. 2000 Transition and chaos in two-dimensional flow past a square cylinder. J. Engng Mech. ASCE 126, 523–532.CrossRefGoogle Scholar
Saha, A. K., Biswas, G. & Muralidhar, K. 2003 Three-dimensional study of flow past a square cylinder at low Reynolds numbers. Intl J. Heat Fluid Flow 24, 54–66.CrossRefGoogle Scholar
Saha, A. K. 2009 Effect of transitions on flow past a square cylinder at low Reynolds number. J. Engng Mech. ASCE 135, 839–851.CrossRefGoogle Scholar
Sheard, G. J., Fitzgerald, M. J. & Ryan, K. 2009 Cylinders with square cross-section: wake instabilities with incidence angle variation. J. Fluid Mech. 630, 43–69.CrossRefGoogle Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2004 From spheres to circular cylinders: non-axisymmetric transitions in the flow past rings. J. Fluid Mech. 506, 45–78.CrossRefGoogle Scholar
Sohankar, A., Norberg, C. & Davidson, L. 1999 Simulation of three-dimensional flow around a square cylinder at moderate Reynolds numbers. Phys. Fluids 11, 288–306.CrossRefGoogle Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001a The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15, 607–616.CrossRefGoogle Scholar
Thompson, M. C., Leweke, T. & Provansal, M. 2001b Kinematics and dynamics of sphere wake transition. J. Fluids Struct. 15, 575–585.CrossRefGoogle Scholar
Williamson, C. H. K. 1996 Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.CrossRefGoogle Scholar