Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-30T23:52:13.018Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional transition in the wake of two tandem rotating cylinders

Published online by Cambridge University Press:  08 November 2022

Suresh Behara Open the ORCID record for Suresh Behara [Opens in a new window] ,
Venu Chandra  and
N.R. Prashanth
Suresh Behara*
Affiliation:
Department of Mechanical Engineering, Aditya Institute of Technology and Management, Tekkali, AP 532201, India
Venu Chandra
Affiliation:
Department of Civil Engineering, Indian Institute of Technology Madras, Chennai, TN 600036, India
N.R. Prashanth
Affiliation:
ESI Software (India) Pvt. Ltd., 27th Cross, Banashankari 2nd Stage, Bangalore, KA 560070, India
*
Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

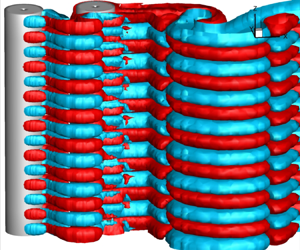
Three-dimensional (3-D) transition in the wake of two tandem co-rotating cylinders is studied numerically for Reynolds numbers $180\le Re\le 500$. Infinite cylinders of equal diameter ($D$) and span ($8D$) are placed at streamwise gaps $Lx=2.5D$ and $7.5D$, and rotated at rotation rates $\alpha =0$, $0.5$, $1$ and $2$. For $\alpha =0$ and $Lx=7.5D$, 3-D transition in the wake of the upstream cylinder resembles that for an isolated cylinder with the formation of Mode-A and Mode-B instabilities, whereas for the downstream cylinder, only Mode-A instability occurs in both the $Lx=2.5D$ and $7.5D$ cases with $\alpha =0$. When the cylinders rotate at $\alpha =1$ for $Lx=7.5D$, staggered transition takes place with the appearance of only Mode-B and only Mode-A instabilities in the near-wake regions of the upstream and downstream bodies, respectively. In the case $Lx=2.5D$, the wake of the rotating cylinders transitions via Mode-C and Mode-D instabilities for $\alpha =0.5$, Mode-D and Mode-D$^\prime$ for $\alpha =1$, and Mode-C and Mode-A for $\alpha =2$. A sudden decrease in near-wake fluctuations, accompanied by a downward jump in the force coefficients, is observed as the 3-D instability shifts from one mode to another, for $\alpha \ge 1$ and $Lx=2.5D$. This discontinuity is caused by the formation of a pair of opposite-signed recirculation zones that mitigate each other's effects in the near-wake region.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex instability Vortex Flows: Vortex interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 951 , 25 November 2022 , A29
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Present address: GE Research, John F. Welch Technology Centre, Bangalore 560066, India.

References

REFERENCES

Akoury, R.E., Braza, M., Perrin, R., Harran, G. & Hoarau, Y. 2008 The three-dimensional transition in the flow around a rotating cylinder. J. Fluid Mech. 607, 1–11.CrossRefGoogle Scholar
Barkley, D. & Henderson, R. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Behara, S. & Mittal, S. 2009 Parallel finite element computation of incompressible flows. Parallel Comput. 35, 195–212.CrossRefGoogle Scholar
Behara, S. & Mittal, S. 2010 a Flow past a circular cylinder at low Reynolds number: oblique vortex shedding. Phys. Fluids 22, 054102.CrossRefGoogle Scholar
Behara, S. & Mittal, S. 2010 b Wake transition in the flow past a circular cylinder. Phys. Fluids 22, 114104.CrossRefGoogle Scholar
Blackburn, H.M., Marques, F. & Lopez, J.M. 2005 Symmetry breaking of two-dimensional time-periodic wakes. J. Fluid Mech. 552, 395–411.CrossRefGoogle Scholar
Braza, M., Faghani, D. & Persillon, H. 2001 Successive stages and the role of natural vortex dislocations in three-dimensional wake transition. J. Fluid Mech. 439, 1–41.CrossRefGoogle Scholar
Carmo, B.S. & Meneghini, J.R. 2006 Numerical investigation of the flow around two circular cylinders in tandem. J. Fluids Struct. 22, 979–988.CrossRefGoogle Scholar
Carmo, B.S., Meneghini, J.R. & Sherwin, S. 2010 Secondary instabilities in the flow around two circular cylinders in tandem. J. Fluid Mech. 644, 395–431.CrossRefGoogle Scholar
Deng, J., Ren, A.-L., Zou, J.-F. & Shao, X.-M. 2006 Three-dimensional flow around two circular cylinders in tandem arrangement. Fluid Dyn. Res. 38, 386–404.CrossRefGoogle Scholar
Henderson, R. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.CrossRefGoogle Scholar
Leweke, T. & Williamson, C.H.K. 1998 Cooperative elliptic instability of a vortex pair. J. Fluid Mech. 360, 85–119.CrossRefGoogle Scholar
Meneghini, J.R., Saltara, F., Siqueira, C.L.R. & Ferrari, J.A. Jr. 2001 Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements. J. Fluids Struct. 15, 327–350.CrossRefGoogle Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.CrossRefGoogle Scholar
Persillon, H. & Braza, M. 1998 Physical analysis of the transition to turbulence in the wake of a circular cylinder by three-dimensional Navier–Stokes simulation. J. Fluid Mech. 365, 23–88.CrossRefGoogle Scholar
Rao, A., Leontini, J.S., Thompson, M.C. & Hourigan, K. 2013 Three-dimensionality in the wake of a rotating cylinder in a uniform flow. J. Fluid Mech. 717, 1–29.CrossRefGoogle Scholar
Rao, A., Radi, A., Leontini, J.S., Thompson, M.C., Sheridan, J. & Hourigan, K. 2015 A review of rotating cylinder wake transitions. J. Fluids Struct. 53, 2–14.CrossRefGoogle Scholar
Saad, Y. & Schultz, M. 1986 GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7, 856–869.CrossRefGoogle Scholar
Schlichting, H. & Gersten, G. 2017 Boundary Layer Theory. Springer.CrossRefGoogle Scholar
Sheard, G., Thompson, M.C. & Hourigan, K. 2003 A coupled Landau model describing the Strouhal–Reynolds number profile of a three-dimensional circular cylinder wake. Phys. Fluids 15, L68.CrossRefGoogle Scholar
Tezduyar, T.E. & Sathe, S. 2003 Stabilization parameters in SUPG and PSPG formulations. J. Comput. Appl. Mech. 4, 71–88.Google Scholar
Thompson, M.C., Leweke, T. & Williamson, C.H.K. 2001 The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15, 607–616.CrossRefGoogle Scholar
Wang, S., Tian, F., Jia, L., Lu, X. & Yin, X. 2010 Secondary vortex street in the wake of two tandem circular cylinders at low Reynolds number. Phys. Rev. E 81, 036305.CrossRefGoogle ScholarPubMed
Williamson, C.H.K. 1996 a Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 b Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.CrossRefGoogle Scholar
Zdravkovich, M.M. 1977 Review of flow interference between two circular cylinders in various arrangements. Trans. ASME J. Fluids Engng 99, 618–633.CrossRefGoogle Scholar
Zdravkovich, M.M. 1987 The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1, 239–261.CrossRefGoogle Scholar
Zhang, H., Fey, U., Noack, B.R., Konig, M. & Eckelmann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7, 779.CrossRefGoogle Scholar