Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T15:27:40.623Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional flow within shallow, narrow cavities

Published online by Cambridge University Press:  28 October 2013

Sarah D. Crook ,
Timothy C. W. Lau  and
Richard M. Kelso
Sarah D. Crook
Affiliation:
Nova Systems, Edinburgh, SA 5111, Australia
Timothy C. W. Lau*
Affiliation:
Centre for Energy Technology, School of Mechanical Engineering, The University of Adelaide, SA 5005, Australia
Richard M. Kelso
Affiliation:
Centre for Energy Technology, School of Mechanical Engineering, The University of Adelaide, SA 5005, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

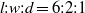The three-dimensional structure of incompressible flow in a narrow, open rectangular cavity in a flat plate was investigated with a focus on the flow topology of the time-averaged flow. The ratio of cavity length (in the direction of the flow) to width to depth was $l{: }w{: }d= 6{: }2{: }1$. Experimental surface pressure data (in air) and particle image velocimetry data (in water) were obtained at low speed with free-stream Reynolds numbers of 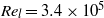${\mathit{Re}}_{l} = 3. 4\times 1{0}^{5} $ in air and 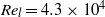${\mathit{Re}}_{l} = 4. 3\times 1{0}^{4} $ in water. The experimental results show that the three-dimensional cavity flow is of the ‘open’ type, with an overall flow structure that bears some similarity to the structure observed in nominally two-dimensional cavities, but with a high degree of three-dimensionality both in the flow near the walls and in the unsteady behaviour. The defining features of an open-type cavity flow include a shear layer that traverses the entire cavity opening ultimately impinging on the back surface of the cavity, and a large recirculation zone within the cavity itself. Other flow features that have been identified in the current study include two vortices at the back of the cavity, of which one is barely visible, a weak vortex at the front of the cavity, and a pair of counter-rotating streamwise vortices along the sides of the cavity near the cavity opening. These vortices are generally symmetric about the cavity centre-plane. However, the discovery of a single tornado vortex, located near the cavity centreline at the front of the cavity, indicated that the flow within the cavity is asymmetric. It is postulated that the observed asymmetry in the time-averaged flow field is due to the asymmetry in the instantaneous flow field, which switches between two extremes at large time scales.

JFM classification

Aerodynamics: Aerodynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 735 , 25 November 2013 , pp. 587 - 612
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashcroft, G. & Zhang, X. 2005 Vortical structures over rectangular cavities at low speed. Phys. Fluids 17, 015104.Google Scholar
Atvars, K., Knowles, K., Ritchie, S. & Lawson, J. 2009 Experimental and computational investigation of an open transonic cavity flow. J. Aerosp. Engng 223, 357–368.Google Scholar
Bian, S., Driscoll, J. F., Elbing, B. R. & Ceccio, S. L. 2011 Time resolved flow field measurements of a turbulent mixing layer over a rectangular cavity. Exp. Fluids 51, 51–63.Google Scholar
Braslow, A., Hicks, R. & Harris, 1966 Use of grit-type boundary-layer-transition trips on wind-tunnel models. NASA Technical Note D-3579.Google Scholar
Charwat, A. F., Foos, J. N., Dewey, F. C. & Hitz, J. A. 1961 An investigation of separated flows. Part 1. The pressure field. J. Aero. Sci. 28 (6), 457–70.Google Scholar
Dix, R. E. & Butler, C. 1990 Cavity aeroacoustics. Tech. Rep. A358322 Oct 85–Apr 90, Calspan Corporation, Arnold Engineering Development Center Operations, Arnold Air Force Base.Google Scholar
Dolling, D. S., Perng, S. W. & Leu, Y. L. 1997 An experimental study of passive control of hypersonic cavity flow oscillations. Tech. Rep. AFRL-SR-BL-TR-98-0240, Center for Aeromechanical Research, University of Texas, Austin.Google Scholar
East, L. F. 1966 Aerodynamic induced resonance in rectangular cavities. J. Sound Vib. 3 (3), 277–287.Google Scholar
Faure, T., Adrianos, P., Lusseyran, F. & Pastur, L. 2007 Visualisation of the flow inside and open cavity at medium range Reynolds numbers. Exp. Fluids 42, 169–184.Google Scholar
Forestier, N., Jacquin, L. & Geffory, P. 2003 The mixing layer over a deep cavity at high-subsonic speed. J. Fluid Mech. 475, 110–145.CrossRefGoogle Scholar
Haigermoser, C., Scarano, F., Onorato, M., Torino, P. & Delft, T. 2008a Investigation of the flow in a rectangular cavity using tomographic and time-resolved PIV. In 26th International Congress of the Aeronautical Science, Anchorage, Alaska, 14–19 September 2008.Google Scholar
Haigermoser, C., Vesely, L., Novara, M. & Onorato, M. 2008b A time-resolved particle image velocimetry investigation of a cavity flow with a thick incoming turbulent boundary layer. Phys. Fluids 20, 105101.Google Scholar
Karamecheti, K. 1956 Sound radiated from surface cutouts in high-speed flows. PhD thesis, California Institute of Technology.Google Scholar
Knowles, K., Ritchie, S. & Lawson, J. 2007 An experimental and computational investigation of a 3D, $l/ h= 5$ transonic cavity flow. In 3rd International Symposium on Integrating CFD and Experiments in Aerodynamics. US Air Force Academy.Google Scholar
Larcheveque, L., Sagaut, P. & Labbe, O. 2007 Large-eddy simulation of subsonic cavity flow including asymmetric three-dimensional effects. J. Fluid Mech. 577, 105–126.Google Scholar
Larcheveque, L., Sagaut, P., Le, T.-H. & Comte, P. 2004 Large-eddy simulation of a compressible flow in a three-dimensional open cavity at high Reynolds number. J. Fluid Mech. 516, 265–301.CrossRefGoogle Scholar
Larsson, J. 2002 Computational aero acoustics for vehicle applications. PhD thesis, Chalmers University of Technology.Google Scholar
Manovski, P., Giacobello, J. & M. Soria, 2008 Particle image velocimetry measurements over an aerodynamically open two-dimensional cavity. In Proceedings of the 5th Australian Conference on Laser Diagnostics in Fluid Mechanics & Combustion, University of Western Australia, 3–4 December.Google Scholar
Mary, I. & Le, T.-H. 2005 Large-eddy simulations of flow past weapons bay. In AVT-123 Symposium on Flow Induced Unsteady Loads and The Impact of Military Applications.Google Scholar
Maull, D. & East, L. F. 1963 Three-dimensional flow in cavities. J. Fluid Mech. 16 (4), 620–632.Google Scholar
Milbank, J. 2004 Investigation of fluid-dynamic cavity oscillations and the effect of flow angle in an automotive context using an open-jet wind tunnel. PhD thesis, RMIT University.Google Scholar
Ozsoy, E., Rambaud, P., Stitou, A. & Riethmuller, M. 2005 Vortex characteristics in laminar cavity flow at very low Mach number. Exp. Fluids 38, 133–145.CrossRefGoogle Scholar
Plumblee, H. E., Gibson, J. S. & Lassiter, L. W. 1962 A theoretical and experimental investigation of the acoustic response of cavities in an aerodynamic flow. Tech. Rep. Wright-Patterson Air Force Base, Technical Report WADD-TR-61-75.Google Scholar
Raffel, M., Willert, C. & Kompenhans, J. 1998 Particle Image Velocimetry: A Practical Guide, 3rd edn. Springer.CrossRefGoogle Scholar
Reihman, T. C. 1967 Laminar flow over transverse rectangular cavities. PhD thesis, California Institute of Technology.Google Scholar
Rossiter, J. E. 1964 Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds. Royal Aircraft Establishment, ARC Reports and Memoranda 3438.Google Scholar
Ruderich, R. & Fernholz, H. 1986 An experimental investigation of a turbulent shear flow with separation, reverse flow, and reattachment. J. Fluid Mech. 163, 283–322.CrossRefGoogle Scholar
Sarohia, V. 1977 Experimental investigation of oscillations in flows over shallow cavities. AIAA J. 15 (7), 984–991.CrossRefGoogle Scholar
Stallings, R. L. & Wilcox, F. 1987 Experimental cavity pressure distributions at supersonic speed. NASA Technical Paper 2683, Langley Research Centre, Hampton, Virginia.Google Scholar
Thwaites, B. 1949 Approximate calculations of the laminar boundary layer. Aeronaut. Q. 1, 245–280.Google Scholar
Tracy, M. & Plentovish, E. 1993 Characterization of cavity flow fields using pressure data obtained in the Langley 0.3-meter transonic cryogenic tunnel. NASA Technical Memorandum 4436, Langley Research Centre, Hampton, Virginia.Google Scholar
Ukeiley, L. & Murray, N. 2005 Velocity and surface pressure measurements in an open cavity. Exp. Fluids 38, 656–671.CrossRefGoogle Scholar
Westerweel, J. & Scarano, F. 2005 Universal outlier detection for PIV data. Exp. Fluids 36, 1096–1100.Google Scholar
Wilcox, F. Jr 1990 Experimental measurements of internal store separation characteristics at supersonic speeds. In Store Carriage, Integration and Release Conference, pp. 5.1–5.16. Royal Aeronautical Society.Google Scholar
Wilcox, F. Jr 1992 Use of a coloured water flow visualization technique in a supersonic wind tunnel to investigate cavity flow fields. In Flow Visualization VI: Proceedings of the Sixth International Symposium on Flow Visualization, p. 4145 Springer.Google Scholar
Yao, H., Cooper, R. & Raghunathan, S. 2004 Numerical simulation of incompressible laminar flow over three-dimensional rectangular cavities. Trans. ASME: J. Fluids Engng 126, 919–927.Google Scholar
Zdanski, P., Ortega, M., Nide, G. & Fico, Jr 2003 Numerical study of the flow over shallow cavities. Comput. Fluids 32, 953–974.CrossRefGoogle Scholar