Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-29T00:51:02.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional flow past a rotating cylinder

Published online by Cambridge University Press:  30 January 2015

Navrose ,
Jagmohan Meena  and
Sanjay Mittal
  Navrose
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Kanpur, UP 208016, India
Jagmohan Meena
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Kanpur, UP 208016, India
Sanjay Mittal*
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Kanpur, UP 208016, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Three-dimensional computations are carried out for a spinning cylinder placed in a uniform flow. The non-dimensional rotation rate is varied in the range 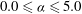$0.0\leqslant {\it\alpha}\leqslant 5.0$ . A stabilized finite element method is utilized to solve the incompressible Navier–Stokes equations in primitive variables formulation. Linear stability analysis of the steady state shows the existence of several new unstable three-dimensional modes for 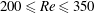$200\leqslant \mathit{Re}\leqslant 350$ and 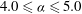$4.0\leqslant {\it\alpha}\leqslant 5.0$ . The curves of neutral stability of these modes are presented in the 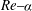$\mathit{Re}{-}{\it\alpha}$ parameter space. 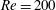For the flow at $\mathit{Re}=200$ and rotation rate in the ranges 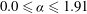$0.0\leqslant {\it\alpha}\leqslant 1.91$ and 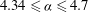$4.34\leqslant {\it\alpha}\leqslant 4.7$ , the vortex shedding, earlier reported in two dimensions and commonly referred to as parallel shedding, can also exist as oblique shedding. In this mode of shedding, the vortices are inclined to the axis of the cylinder. In fact, parallel shedding is a special case of oblique shedding. It is found that the span of the cylinder plays a significant role in the time evolution of the flow. Of all the unstable eigenmodes, with varied spanwise wavenumber, only the ones whose integral number of wavelengths fit the span length of the cylinder are selected to grow. 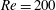For the flow at $\mathit{Re}=200$ , two steady states exist for 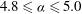$4.8\leqslant {\it\alpha}\leqslant 5.0$ . While one of them is associated with unstable eigenmodes, the other is stable to all infinitesimal perturbations. In this regime, irrespective of the initial conditions, the fully developed flow is steady and devoid of any instabilities.

JFM classification

Instability: Parametric instability Vortex Flows: Vortex shedding Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 766 , 10 March 2015 , pp. 28 - 53
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Barnes, F. H. 2000 Vortex shedding in the wake of a rotating circular cylinder at low Reynolds number. J. Phys. D: Appl. Phys. 33, L141–L144.CrossRefGoogle Scholar
Bayly, B. J. 1988 Three dimensional centrifugal-type instabilities in inviscid two-dimensional flows. Phys. Fluids 31, 56–64.Google Scholar
Behara, S. & Mittal, S. 2009 Parallel finite element computation of incompressible flows. Parallel Comput. 35, 195–212.Google Scholar
Berger, E. & Wille, R. 1972 Periodic flow phenomena. Annu. Rev. Fluid Mech. 4, 313–340.Google Scholar
El Akoury, R., Braza, M., Perrin, R., Harran, G. & Hoarau, Y. 2008 The three-dimensional transition in the flow around a rotating cylinder. J. Fluid Mech. 607, 1–11.CrossRefGoogle Scholar
Gerich, D. & Eckelmann, H. 1982 Influence of end plates and free ends on the shedding frequency of circular cylinders. J. Fluid Mech. 122, 109–121.CrossRefGoogle Scholar
Hu, G.-H., Sun, D.-J., Yin, X.-Y. & Tong, B.-G. 1996 Hopf bifurcation in wakes behind a rotating and translating circular cylinder. Phys. Fluids 8 (7), 1972–1974.Google Scholar
Ingham, D. B. 1983 Steady flow past a rotating cylinder. Comput. Fluids 11 (4), 351–366.Google Scholar
Kang, S. M., Choi, H. C. & Lee, S. 1999 Laminar flow past a rotating circular cylinder. Phys. Fluids 11 (11), 3312–3321.CrossRefGoogle Scholar
Meena, J.2011 Three-dimensional instabilities in flow past a rotating cylinder. M.Tech. thesis, Department of Aerospace Engineering, Indian Institute of Technology, Kanpur.Google Scholar
Meena, J., Sidharth, G. S., Khan, M. H. & Mittal, S.2011 Three-dimensional instabilities in flow past a spinning and translating cylinder. In IUTAM Symposium on Bluff Body Flows, IIT Kanpur, India (ed. S. Mittal & G. Biswas), Book of Papers, pp. 59–62.Google Scholar
Mittal, S. 2004 Three-dimensional instabilities in flow past a rotating cylinder. Trans. ASME: J. Appl. Mech. 71 (1), 89–95.Google Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.Google Scholar
Mittal, S. & Sidharth, G. S. 2013 Steady forces on a cylinder with oblique vortex shedding. J. Fluids Struct. 44, 310–315.CrossRefGoogle Scholar
Padrino, J. C. & Joseph, D. D. 2006 Numerical study of the steady-state uniform flow past a rotating cylinder. J. Fluid Mech. 557, 191–223.Google Scholar
Pralits, J. O., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.Google Scholar
Pralits, J. O., Giannetti, F. & Brandt, L. 2013 Three-dimensional instability of the flow around a rotating circular cylinder. J. Fluid Mech. 730, 5–18.CrossRefGoogle Scholar
Radi, A., Thompson, M. C., Rao, A., Hourigan, K. & Sheridan, J. 2013 Experimental evidence of new three-dimensional modes in the wake of a rotating cylinder. J. Fluid Mech. 734, 567–594.Google Scholar
Rao, A., Leontini, J., Thompson, M. C. & Hourigan, K. 2013a Three-dimensionality in the wake of a rotating cylinder in a uniform flow. J. Fluid Mech. 717, 1–29.Google Scholar
Rao, A., Leontini, J., Thompson, M. C. & Hourigan, K. 2013b Three-dimensionality in the wake of a rapidly rotating cylinder in uniform flow. J. Fluid Mech. 730, 379–391.Google Scholar
Rao, A., Radi, A., Leontini, J., Thompson, M. C., Sheridan, J. & Hourigan, K. 2014 A review of rotating cylinder wake transitions. J. Fluids Struct. Google Scholar
Rayleigh, Lord 1917 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–154.Google Scholar
Saad, Y. & Schultz, M. H. 1986 GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7 (3), 856–869.Google Scholar
Stewart, G. W. 1975 Methods of simultaneous iteration for calculating eigenvectors of matrices. In Topics in Numerical Analysis II (ed. Miller, J. H. H.), pp. 169–185. Academic.Google Scholar
Stojković, D., Breuer, M. & Durst, F. 2002 Effect of high rotation rates on the laminar flow around a circular cylinder. Phys. Fluids 14 (9), 3160–3178.Google Scholar
Stojković, D., Schön, P., Breuer, M. & Durst, F. 2003 On the new vortex shedding mode past a rotating circular cylinder. Phys. Fluids 15 (5), 1257–1260.Google Scholar
Tezduyar, T. C., Mittal, S., Ray, S. E. & Shih, R. 1992 Incompressible flow computations with a stabilized bilinear and linear equal-order-interpolation velocity–pressure elements. Comput. Meth. Appl. Mech. Engng 95, 221–242.Google Scholar
Tritton, D. J. 1971 A note on vortex streets behind circular cylinders at low Reynolds numbers. J. Fluid Mech. 45, 203–208.Google Scholar
Verma, A. & Mittal, S. 2011 A new unstable mode in the wake of a circular cylinder. Phys. Fluids 23 (12), 121701.Google Scholar
Williamson, C. H. K. 1989 Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 206, 579–627.Google Scholar
Williamson, C. H. K. 1996 Three dimensional vortex dynamics in bluff body wakes. Exp. Therm. Fluid Sci. 12, 150–168.Google Scholar