Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-03T00:37:03.276Z Has data issue: false hasContentIssue false
  • English
  • Français

A three-component model for the coupled evolution of near-inertial waves, quasi-geostrophic flow and the near-inertial second harmonic

Published online by Cambridge University Press:  10 August 2016

G. L. Wagner Open the ORCID record for G. L. Wagner [Opens in a new window]  and
W. R. Young
G. L. Wagner*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, La Jolla, CA 90293-0411, USA
W. R. Young
Affiliation:
Scripps Institution of Oceanography, University of California San Diego, La Jolla, CA 90293-0213, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

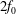We derive an asymptotic model that describes the nonlinear coupled evolution of (i) near-inertial waves (NIWs), (ii) balanced quasi-geostrophic flow and (iii) near-inertial second harmonic waves with frequency near $2f_{0}$, where 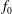$f_{0}$ is the local inertial frequency. This ‘three-component’ model extends the two-component model derived by Xie & Vanneste (J. Fluid Mech., vol. 774, 2015, pp. 143–169) to include interactions between near-inertial and 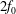$2f_{0}$ waves. Both models possess two conservation laws which together imply that oceanic NIWs forced by winds, tides or flow over bathymetry can extract energy from quasi-geostrophic flows. A second and separate implication of the three-component model is that quasi-geostrophic flow catalyses a loss of NIW energy to freely propagating waves with near-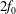$2f_{0}$ frequency that propagate rapidly to depth and transfer energy back to the NIW field at very small vertical scales. The upshot of near-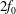$2f_{0}$ generation is a two-step mechanism whereby quasi-geostrophic flow catalyses a nonlinear transfer of near-inertial energy to the small scales of wave breaking and diapycnal mixing. A comparison of numerical solutions with both Boussinesq and three-component models for a two-dimensional initial value problem reveals strengths and weaknesses of the model while demonstrating the extraction of quasi-geostrophic energy and production of small vertical scales.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Ocean processes Geophysical and Geological Flows: Quasi-geostrophic flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 802 , 10 September 2016 , pp. 806 - 837
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balmforth, N. J., Smith, S. L. & Young, W. R. 1998 Enhanced dispersion of near-inertial waves in an idealized geostrophic flow. J. Mar. Res. 56 (1), 1–40.Google Scholar
Balmforth, N. J. & Young, W. R. 1999 Radiative damping of near-inertial oscillations in the mixed layer. J. Mar. Res. 57 (4), 561–584.Google Scholar
Bühler, O. & McIntyre, M. E. 1998 On non-dissipative wave–mean interactions in the atmosphere or oceans. J. Fluid Mech. 354, 609–646.Google Scholar
Cox, S. M. & Matthews, P. C. 2002 Exponential time differencing for stiff systems. J. Comput. Phys. 176 (2), 430–455.Google Scholar
Danioux, E. & Klein, P. 2008 A resonance mechanism leading to wind-forced motions with a 2f frequency. J. Phys. Oceanogr. 38 (10), 2322–2329.Google Scholar
Danioux, E., Klein, P. & Rivière, P. 2008 Propagation of wind energy into the deep ocean through a fully turbulent mesoscale eddy field. J. Phys. Oceanogr. 38 (10), 2224–2241.Google Scholar
Danioux, E., Vanneste, J. & Bühler, O. 2015 On the concentration of near-inertial waves in anticyclones. J. Fluid Mech. 773, R2.Google Scholar
D’Asaro, E. A., Eriksen, C. C., Levine, M. D., Paulson, C. A., Niiler, P. P. & van Meurs, P. 1995 Upper-ocean inertial currents forced by a strong storm. Part I: data and comparisons with linear theory. J. Phys. Oceanogr. 25, 2909–2936.Google Scholar
Falkovich, G., Kuznetsov, E. & Medvedev, S. 1994 Nonlinear interaction between long inertio-gravity and Rossby waves. Nonlinear Process. Geophys. 1, 168–171.Google Scholar
Ferrari, R. & Wunsch, C. 2009 Ocean circulation kinetic energy: reservoirs, sources, and sinks. Annu. Rev. Fluid Mech. 41, 253–282.Google Scholar
Gertz, A. & Straub, D. N. 2009 Near-inertial oscillations and the damping of midlatitude gyres: a modeling study. J. Phys. Oceanogr. 39 (9), 2338–2350.Google Scholar
Grooms, I. & Julien, K. 2011 Linearly implicit methods for nonlinear PDEs with linear dispersion and dissipation. J. Comput. Phys. 230 (9), 3630–3650.Google Scholar
Kassam, A.-K. & Trefethen, L. N. 2005 Fourth-order time-stepping for stiff pdes. SIAM J. Sci. Comput. 26 (4), 1214–1233.Google Scholar
Klein, P. & Smith, S. L. 2001 Horizontal dispersion of near-inertial oscillations in a turbulent mesoscale eddy field. J. Mar. Res. 59, 697–723.Google Scholar
Klein, P., Smith, S. L. & Lapeyre, G. 2004 Organization of near-inertial energy by an eddy field. Q. J. R. Meteorol. Soc. 130, 1153–1166.Google Scholar
Kunze, E. 1985 Near inertial wave propagation in geostrophic shear. J. Phys. Oceanogr. 15, 544–565.Google Scholar
Lee, D.-K. & Niiler, P. P. 1998 The inertial chimney: the near-inertial energy drainage from the ocean surface to the deep layer. J. Geophys. Res. 103 (C4), 7579–7591.Google Scholar
Mooers, C. N. K. 1975 Several effects of a baroclinic current on the cross-stream propagation of inertial-internal waves. Geophys. Fluid Dyn. 6, 245–275.Google Scholar
Niwa, Y. & Hibiya, T. 1999 Response of the deep ocean internal wave field to traveling midlatitude storms as observed in long-term current measurements. J. Geophys. Res. 104 (C5), 10981–10989.Google Scholar
Roberts, A. J. 1985 An introduction to the technique of reconstitution. SIAM J. Math. Anal. 16 (6), 1243–1257.Google Scholar
Vanneste, J. 2013 Balance and spontaneous wave generation in geophysical flows. Annu. Rev. Fluid Mech. 45, 147–172.Google Scholar
Wagner, G. L. & Young, W. R. 2015 Available potential vorticity and wave-averaged quasi-geostrophic flow. J. Fluid Mech. 785, 401–424.Google Scholar
Winters, K. B., MacKinnon, J. A. & Mills, B. 2004 A spectral model for process studies of rotating, density-stratified flows. J. Atmos. Ocean. Technol. 21 (1), 69–94.Google Scholar
Xie, J.-H. & Vanneste, J. 2015 A generalised Lagrangian-mean model of the interactions between near-inertial waves and mean flow. J. Fluid Mech. 774, 143–169.Google Scholar
Young, W. R. & Ben Jelloul, M. 1997 Propagation of near-inertial oscillations through a geostrophic flow. J. Mar. Res. 55 (4), 735–766.Google Scholar
Young, W. R., Tsang, Y.-K. & Balmforth, N. J. 2008 Near-inertial parametric subharmonic instability. J. Fluid Mech. 607, 25–49.Google Scholar
Zeitlin, V., Reznik, G. M. & Ben Jelloul, M. 2003 Nonlinear theory of geostrophic adjustment. Part 2. Two-layer and continuously stratified primitive equations. J. Fluid Mech. 491, 207–228.Google Scholar