Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T16:44:26.500Z Has data issue: false hasContentIssue false
  • English
  • Français

Three regimes of inertial focusing for spherical particles suspended in circular tube flows

Published online by Cambridge University Press:  30 May 2019

Saki Nakayama ,
Hiroshi Yamashita ,
Takuya Yabu ,
Tomoaki Itano  and
Masako Sugihara-Seki Open the ORCID record for Masako Sugihara-Seki [Opens in a new window]
Saki Nakayama
Affiliation:
Kansai University, Department of Pure and Applied Physics, 3-3-35 Yamate-cho, Suita, Osaka 564-8680, Japan
Hiroshi Yamashita
Affiliation:
Kansai University, Department of Pure and Applied Physics, 3-3-35 Yamate-cho, Suita, Osaka 564-8680, Japan
Takuya Yabu
Affiliation:
Kansai University, Department of Pure and Applied Physics, 3-3-35 Yamate-cho, Suita, Osaka 564-8680, Japan
Tomoaki Itano
Affiliation:
Kansai University, Department of Pure and Applied Physics, 3-3-35 Yamate-cho, Suita, Osaka 564-8680, Japan
Masako Sugihara-Seki*
Affiliation:
Kansai University, Department of Pure and Applied Physics, 3-3-35 Yamate-cho, Suita, Osaka 564-8680, Japan Osaka University, Graduate School of Engineering Science, 1-3 Machikaneyama-cho, Toyonaka, Osaka 560-8531, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

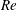An experimental and numerical study on the inertial focusing of neutrally buoyant spherical particles suspended in laminar circular tube flows was performed at Reynolds numbers ($Re$) ranging from 100 to 1000 for particle-to-tube diameter ratios of 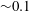${\sim}0.1$. In the experiments, we measured the cross-sectional distribution of particles in dilute suspensions flowing through circular tubes several hundreds of micrometres in diameter. In the cross-section located at 1000 times the tube diameter from the tube inlet, all particles were highly concentrated on one annulus or two annuli, depending on 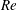$Re$. At low 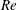$Re$, the particles were focused on the so-called Segré–Silberberg (SS) annulus, in accordance with previous studies (regime (A)). At higher 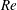$Re$, two particle focusing annuli appeared, with the outer annulus corresponding to the SS annulus (regime (B)). We call the annulus closer to the tube centre ‘the inner annulus’, although this term was used by Matas et al. (J. Fluid Mech., vol. 515, 2004, pp. 171–195) for a significantly broader annulus which included the transient accumulation of particles observed in regime (A). At even higher 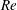$Re$, particles were focused on the inner annulus (regime (C)), indicating that the radial position of the SS annulus is no longer a stable equilibrium position. These experimental results were confirmed by a numerical simulation based on the immersed boundary method. The results of this study also indicate that the critical Reynolds numbers between two neighbouring regimes decrease with the increase of the particle-to-tube diameter ratio.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , pp. 952 - 969
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asmolov, E. S. 1999 The inertial lift on a spherical particle in a plane Poiseuille flow at large channel Reynolds number. J. Fluid Mech. 381, 63–87.10.1017/S0022112098003474Google Scholar
Barkley, D. 2016 Theoretical perspective on the route to turbulence in a pipe. J. Fluid Mech. 803, P1.10.1017/jfm.2016.465Google Scholar
Deguchi, K. & Walton, A. G. 2013 A swirling spiral wave solution in pipe flow. J. Fluid Mech. 737, R2.10.1017/jfm.2013.582Google Scholar
Kajishima, T., Takiguchi, S., Hamasaki, H. & Miyake, Y. 2001 Turbulence structure of particle-laden flow in a vertical plane channel due to vortex shedding. JSME Intl J. B44, 526–535.10.1299/jsmeb.44.526Google Scholar
Matas, J.-P., Morris, J. F. & Guazzelli, E. 2003 Transition to turbulence in particulate pipe flow. Phys. Rev. Lett. 90, 014501.10.1103/PhysRevLett.90.014501Google Scholar
Matas, J.-P., Morris, J. F. & Guazzelli, E. 2004 Inertial migration of rigid spherical particles in Poiseuille flow. J. Fluid Mech. 515, 171–195.10.1017/S0022112004000254Google Scholar
Matas, J.-P., Morris, J. F. & Guazzelli, E. 2009 Lateral force on a rigid sphere in large-inertia laminar pipe flow. J. Fluid Mech. 621, 59–67.10.1017/S0022112008004977Google Scholar
Morita, Y., Itano, T. & Sugihara-Seki, M. 2017 Equilibrium radial positions of neutrally buoyant spherical particles over the circular cross-section in Poiseuille flow. J. Fluid Mech. 813, 750–767.10.1017/jfm.2016.881Google Scholar
Nakagawa, N., Yabu, T., Otomo, R., Kase, A., Makino, M., Itano, T. & Sugihara-Seki, M. 2015 Inertial migration of a spherical particle in laminar square channel flows from low to high Reynolds numbers. J. Fluid Mech. 779, 776–793.10.1017/jfm.2015.456Google Scholar
Nishi, M., Ünsal, B., Durst, F. & Biswas, G. 2008 Laminar-to-turbulent transition of pipe flows through puffs and slugs. J. Fluid Mech. 614, 425–446.10.1017/S0022112008003315Google Scholar
Pringle, C. C. T. & Kerswell, R. R. 2007 Asymmetric, helical and mirror-symmetric travelling waves in pipe flow. Phys. Rev. Lett. 99, 074502.10.1103/PhysRevLett.99.074502Google Scholar
Schonberg, J. A. & Hinch, E. J. 1989 Inertial migration of a sphere in Poiseuille flow. J. Fluid Mech. 203, 517–524.10.1017/S0022112089001564Google Scholar
Segré, G. & Silberberg, A. 1961 Radial particle displacements in Poiseuille flow of suspensions. Nature 189, 209–210.10.1038/189209a0Google Scholar
Segré, G. & Silberberg, A. 1962 Behaviour of macroscopic rigid spheres in Poiseuille flow. Part 2. Experimental results and interpretation. J. Fluid Mech. 14, 136–157.10.1017/S0022112062001111Google Scholar
Shao, X., Yu, Z. & Sun, B. 2008 Inertial migration of spherical particles in circular Poiseuille flow at moderately high Reynolds numbers. Phys. Fluids 20, 103307.10.1063/1.3005427Google Scholar
Shichi, H., Yamashita, H., Seki, J., Itano, T. & Sugihara-Seki, M. 2017 Inertial migration regimes of spherical particles suspended in submillimeter square tube flows. Phys. Rev. Fluids 2, 044201.10.1103/PhysRevFluids.2.044201Google Scholar
Song, B., Barkley, D., Hof, B. & Avila, M. 2017 Speed and structure of turbulent fronts in pipe flow. J. Fluid Mech. 813, 1045–1059.10.1017/jfm.2017.14Google Scholar
Tritton, D. J. 1988 Physical Fluid Dynamics, 2nd edn. Oxford University Press.Google Scholar
Yang, B. H., Wang, J., Joseph, D. D., Hu, H. H., Pan, T.-W. & Glowinski, R. 2005 Migration of a sphere in tube flow. J. Fluid Mech. 540, 109–131.10.1017/S0022112005005677Google Scholar
Yu, Z., Wu, T., Shao, X. & Lin, J. 2013 Numerical studies of the effects of large neutrally buoyant particles on the flow instability and transition to turbulence in pipe flow. Phys. Fluids 25, 043305.10.1063/1.4802040Google Scholar