No CrossRef data available.
Article contents
Thin-film Rayleigh–Taylor instability in the presence of a deep periodic corrugated wall
Published online by Cambridge University Press: 23 November 2021
Abstract
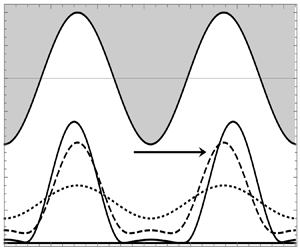
Rayleigh–Taylor instability of a thin liquid film overlying a passive fluid is examined when the film is attached to a periodic wavy deep corrugated wall. A reduced-order long-wave model shows that the wavy wall enhances the instability toward rupture when the interface pattern is sub-harmonic to the wall pattern. An expression that approximates the growth constant of instability is obtained for any value of wall amplitude for the special case when the wall consists of two full waves and the interface consists of a full wave. Nonlinear computations of the interface evolution show that sliding is arrested by the wavy wall if a single liquid film residing over a passive fluid is considered but not necessarily when a bilayer sandwiched by a top wavy wall and bottom flat wall is considered. In the latter case interface tracking shows that primary and secondary troughs will evolve and subsequently slide along the flat wall due to symmetry-breaking. It is further shown that this sliding motion of the interface can ultimately be arrested by the top wavy wall, depending on the holdup of the fluids. In other words, there exists a critical value of the interface position beyond which the onset of the sliding motion is observed and below which the sliding is always arrested.
- Type
- JFM Rapids
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
Dinesh et al. supplementary movie 1
Dinesh et al. supplementary movie 2
Arresting sliding motion of the free surface of a thin layer of water suspended from a wavy wall. Here the initial perturbation is out of phase with the shape of the wavy wall
Dinesh et al. supplementary movie 3
Arresting sliding motion of the free surface of a thin layer of water suspended from a wavy wall. Here the initial perturbation is in phase with the shape of the wavy wall
Dinesh et al. supplementary movie 4
Sliding of the interface between silicone oil (1.5 cSt bottom layer) and water (top layer) as the interface approaches the wall. Here the sliding motion is arrested due to the presence of a wavy wall



