Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T15:24:23.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Thin power-law film flow down an inclined plane: consistent shallow-water models and stability under large-scale perturbations

Published online by Cambridge University Press:  16 October 2013

Pascal Noble  and
Jean-Paul Vila
Pascal Noble*
Affiliation:
Université de Lyon, Université Lyon I, Institut Camille Jordan, UMR CNRS 5208, 43 boulevard du 11 novembre 1918, 69622 Villeurbanne CEDEX, France
Jean-Paul Vila
Affiliation:
Institut de Mathématiques de Toulouse, UMR CNRS 5219, INSA de Toulouse, 135 avenue de Rangueil, 31077 Toulouse CEDEX 4, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we derive consistent shallow-water equations for the flow of thin films of power-law fluids down an incline. These models account for the streamwise diffusion of momentum, which is important to describe accurately the full dynamics of thin-film flows when instabilities such as roll waves arise. These models are validated through a comparison with the Orr–Sommerfeld equations for large-scale perturbations. We consider only laminar flow for which the boundary layer issued from the interaction of the flow with the bottom surface has an influence all over the transverse direction to the flow. In this case the concept itself of a thin film and its relation with long-wave asymptotics leads naturally to flow conditions around a uniform free-surface Poiseuille flow. The apparent viscosity diverges at the free surface, which, in turn, introduces a singularity in the formulation of the Orr–Sommerfeld equations and in the derivation of shallow-water models. We remove this singularity by introducing a weaker formulation of the Cauchy momentum equations. No regularization procedure is needed, nor any distinction between shear thinning and thickening cases. Our analysis, though, is only valid when the flow behaviour index $n$ is larger than 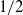$1/ 2$, and strongly suggests that the Cauchy momentum equations are ill-posed if 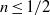$n\leq 1/ 2$.

JFM classification

Geophysical and Geological Flows: Shallow water flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 735 , 25 November 2013 , pp. 29 - 60
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amaouche, M., Djema, A. & Ait Abderrahmane, H. 2012 Film flow for power-law fluids: modeling and linear stability. Eur. J. Mech. (B/Fluids) 34, 70–84.CrossRefGoogle Scholar
Amaouche, M., Djema, A. & Bourdache, L. 2009 A modified Shkadov’s model for thin film flow of a power law fluid over an inclined surface. C. R. Acad. Sci. Méc. 337 (1), 48–52.Google Scholar
Benney, D. J. 1966 Long waves on liquid films. J. Math. Phys. (NY) 45, 50–155.Google Scholar
Berezin, Y. A., Hutter, K. & Spodareva, L. A. 1998 Stability analysis of gravity driven shear flows with free surface for power-law fluids. Arch. Appl. Mech. 68, 169–178.Google Scholar
Boutounet, M., Chupin, L., Noble, P. & Vila, J.-P. 2008 Shallow water equations for Newtonian fluids over arbitrary topographies. Commun. Math. Sci 6 (1), 29–55.Google Scholar
Dandapat, B. S. & Mukhopadhyay, A. 2001 Waves on a film of power-law fluid flowing down an inclined plane at moderate Reynolds number. Fluid Dyn. Res. 29, 199–220.Google Scholar
Dandapat, B. S. & Mukhopadhyay, A. 2003 Waves on the surface of a falling power-law fluid. Intl J. Non-Linear Mech. 38, 21–38.Google Scholar
Dietze, G. F., Leefken, A. & Kneer, R. 2008 Investigation of the backflow phenomenon in falling liquid films. J. Fluid Mech. 595, 435–459.CrossRefGoogle Scholar
Fernandez-Nieto, E. D., Noble, P. & Vila, J.-P. 2010 Shallow water equations for non-Newtonian fluids. J. Non-Newtonian Fluid Mech. 165, 712–732.CrossRefGoogle Scholar
Glen, J. W. 1958 The mechanical properties of ice I. The plastic properties of ice. Adv. Phys. 7 (26), 254–265.Google Scholar
Hwang, C.-C., Chan, J.-L., Wang, J.-S. & Lin, J.-S. 1994 Linear stability of power law liquid film flows down an inclined plane. J. Phys. D: Appl. Phys 27, 2297–2301.CrossRefGoogle Scholar
Kapitza, P. L. & Kapitza, S. P. 1949 Wave flow of thin liquid layers. Zh. Eksp. Teor. Fiz. 19, 105–120.Google Scholar
Liu, J. & Gollub, J. P. 1994 Solitary wave dynamics of film flows. Phys. Fluids 6 (5), 1702–1713.Google Scholar
Malek, J., Necas, J., Rokyta, M. & Ruzicka, M. 1996 Weak and Measure-Valued Solutions to Evolutionary PDEs, Applied Mathematics and Mathematical Computation, vol. 13, Chapman & Hall.Google Scholar
Miladinova, S., Lebon, G. & Toshev, E. 2004 Thin-film flow of a power-law liquid falling down an inclined plate. J. Non-Newtonian Fluid Mech. 122 (1–3), 69–78.CrossRefGoogle Scholar
Ng, C.-O. & Mei, C. C. 1994 Roll waves on a shallow layer of mud modelled as a power-law fluid. J. Fluid Mech. 263, 151–184.Google Scholar
Nye, J. F. 1953 The flow law of ice from measurements in glacier tunnels, laboratory experiments and the Jungfraufirn borehole experiment. Proc. R. Soc. Lond. A 219 (1139), 477–489.Google Scholar
Nye, J. F. 1957 The distribution of stress and velocity in glaciers and ice-sheets. Proc. R. Soc. Lond. Ser. A 239 (1216), 113–133.Google Scholar
Pumir, A., Manneville, P. & Pomeau, Y. 1983 On solitary waves running down on inclined plane. J. Fluid Mech. 135, 27–50.Google Scholar
Rappaz, M., Bellet, M. & Deville, M. 1998 Numerical Modelling in Materials Science and Engineering. Springer.Google Scholar
Richard, G. L. & Gavrilyuk, S. L. 2012 A new model of roll waves: comparison with Brock’s experiments. J. Fluid. Mech. 698, 374–405.Google Scholar
Ruyer-Quil, C., Chakraborty, S. & Dandapat, B. S. 2012 Wavy regime of a power-law film flow. J. Fluid Mech. 692, 220–256.Google Scholar
Ruyer-Quil, C. & Manneville, P. 1998 Modelling film flows down inclined plane. Eur. Phys. J. B 6, 277–298.Google Scholar
Ruyer-Quil, C. & Manneville, P. 2000 Improved modelling of flows down inclined plane. Eur. Phys. J. B 15, 357–369.CrossRefGoogle Scholar
Scheid, B., Ruyer-Quil, C. & Manneville, P. 2006 Wave patterns in film flows: modelling and three-dimensional waves. J. Fluid Mech. 562, 183–222.Google Scholar
Shkadov, V. Y. 1967 Wave conditions in the flow of thin layer of a viscous liquid under the action of gravity. Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 1, 43–51.Google Scholar
Sisoev, G. M., Dandapat, B. S., Matveyev, K. S. & Mukhopadhyay, A. 2007 Bifurcation analysis of the travelling waves on a falling power-law fluid film. J. Non-Newtonian Fluid Mech. 141 (23), 128–137.Google Scholar
Spodareva, L. A. 2000 Stability of non-Newtonian fluid flows. J. Appl. Mech. Tech. Phys. 41, 446–451.CrossRefGoogle Scholar
Usha, R., Millet, S., Ben Hadid, H. & Rousset, F. 2011 Shear-thinning film on a porous substrate: stability analysis of a one-sided model. Chem. Engng Sci. 66, 5614–5627.Google Scholar